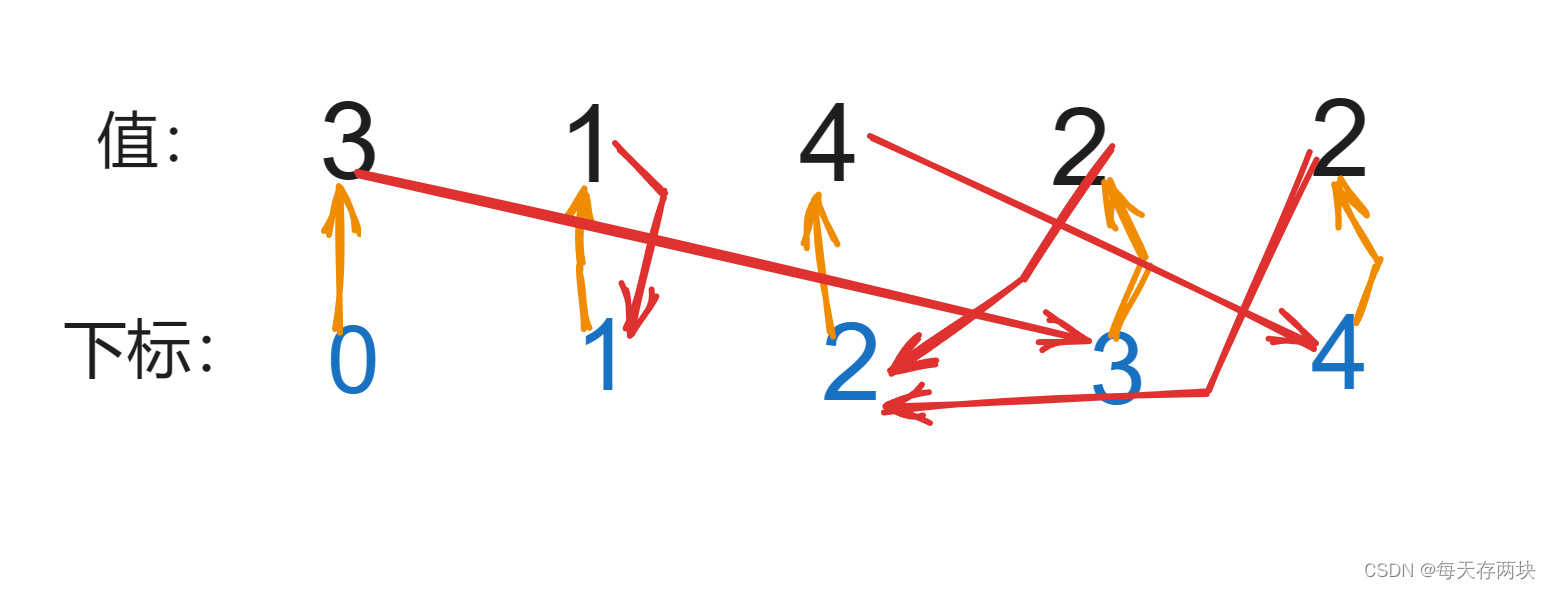
1.前缀和:

前缀和是指某序列的前n项和

2.一维前缀和:

s[i]=a[1]+a[2]+...+a[i],s[r]-s[l-1]=a[l]+...+a[r]

3.前缀和运算

int sum[N],a[N]
for(int i=1;i<=n;i++){
sum[i]=sum[i-1]+a[i];
}

4.查询操作,假设要求序列中第l个数到第r个数的和 ,这样使得查询操作的时间复杂度为O（1）。

sum[r]-sum[l-1]

5.一个模板

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int sum[N], a[N];
int n, m;//n代表序列的长度,m代表询问的次数
int main() {cin >> n >> m;for (int i = 1; i <= n; i++)cin >> a[i];//输入数据for (int i = 1; i <= n; i++)sum[i] = sum[i - 1] + a[i];//前缀和for (int k = 1; k <= m; k++) {int left, right;cin >> left >> right;cout << "区间"<<left<<"到"<<right<<"所有元素和为" << sum[right] - sum[left - 1] << endl;}
}

6.二维前缀和（也可以利用一维的方法)

for (int i = x1; i <= x2; i++) {
    a[i][y1]++;
    a[i][y2 + 1]--;
}

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        a[i][j] += a[i][j - 1];
        cout << a[i][j] << " ";
    }

s[i][j]代表第i行第j列左上部分的所有元素之和.

以(x1,y1)为左上角,(x2,y2)为右下角的子矩阵的和为:s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1],希望下面的图能够帮助你理解。

#include<iostream>
using namespace std;
const int N =1000;
int n, m, k;//n代表行数 m代表列数,k代表询问次数
int s[N][N];
int main() {cin >> n >> m>>k;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> s[i][j];}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];}}cout << endl;while (k--) {int x1, y1, x2, y2;cin >> x1 >> y1 >> x2 >> y2;cout <<'(' << x1 << ',' << y1 << ")到"<<'('<<x2<<','<<y2<<")之间的元素和为:" << s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1] << endl;}return 0;
}

7.差分：求数组中某个区间的元素之和、更新某个区间的元素值等操作，做法:构建一个新的数组,使得新数组的每个元素表示原始数组中相邻元素的差值,这样对差分数组进行一系列操作，可以转换为对原始数组的操作。具体来说，假设有一个原始数组a,长度为n,则差分数组d的长度为n-1，其中d[i]=a[i+1]-a[i]。

8.用途：快速求解数组中某个区间的元素和,高效更新数组中某个区间的元素值..........

9.构造差分数组:

a[0]=0;//a是原数组
b[1]=a[1]-a[0];
b[2]=a[2]-a[1];
......
b[n]=a[n]-a[n-1]

10.问题引入:把数组a中[left,right]区间的每一个元素都加上c,那么也就是a[l]——>a[r]都加上c,这样时间复杂度会很高，我们只需要对其差分数组d操作:d[l]+=c,d[r+1]-=c即可,因为a是d的前缀和数组,d[l]+=c操作,会将a从left开始往后的元素全部+c,d[r+1]-=c操作会对从right+1开始往后的全部元素-c,这样也就是对left——>right之间的元素+c

11.一维差分公式:d[left]+=c,d[right+1]-=c;d是差分数组

12.模板:

#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N], d[N];
int n, m;//n代表a数组的长度,m代表查询次数
int main() {cin >> n >> m;for (int i = 1; i <= n; i++) {cin >> a[i];d[i] = a[i] - a[i - 1];}int left, right, c;while (m--) {cin >> left >> right >> c;d[left] += c;//第一步d[right + 1] -= c;//第二步}//求进行left——>到right区间加c后的数组for (int i = 1; i <= n; i++) {d[i] += d[i-1];cout << d[i]<<" ";}return 0;
}

13.二维差分:原数组:a[][],差分数组d[][]。(a是d的前缀和数组,d是a的差分数组)

14.如何构造差分数组d:d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]。理解了二维数组前缀和就可以明白这个。

15.模板:

#include<iostream>
using namespace std;
const int N = 1000;
int a[N][N], d[N][N];
int main() {int n, m, q;cin >> n >> m>>q;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cin >> a[i][j];}}//构建差分数组for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {d[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];}}while (q--) {int x1, y1, x2, y2, c;cin >> x1 >> y1 >> x2 >> y2 >> c;d[x1][y1] += c;d[x1][y2 + 1] -= c;d[x2 + 1][y1] -= c;d[x2 + 1][y2 + 1] += c;}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {d[i][j] += d[i - 1][j] + d[i][j - 1] - d[i - 1][j - 1];}}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {cout << d[i][j] << " ";}cout << endl;}return 0;
}

最后一些相关例题

P3131 [USACO16JAN] Subsequences Summing to Sevens S - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

P1387 最大正方形 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

P3397 地毯 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)