DS图—图的最短路径/Dijkstra算法【数据结构】
题目描述
给出一个图的邻接矩阵,输入顶点v,用迪杰斯特拉算法求顶点v到其它顶点的最短路径。
输入
第一行输入t,表示有t个测试实例
第二行输入顶点数n和n个顶点信息
第三行起,每行输入邻接矩阵的一行,以此类推输入n行
第i个结点与其它结点如果相连则为距离,无连接则为0,数据之间用空格隔开。
第四行输入一个顶点v,表示求该顶点v到其他顶点的最短路径距离
以此类推输入下一个示例
输出
对每组测试数据,输出:
每行输出顶点v到某个顶点的最短距离和最短路径
每行格式:顶点v编号-其他顶点编号-最短路径值----[最短路径]。没有路径输出:顶点v编号-其他顶点编号–1。具体请参考示范数据
输入样例1
2
5 0 1 2 3 4
0 5 0 7 15
0 0 5 0 0
0 0 0 0 1
0 0 2 0 0
0 0 0 0 0
0
6 V0 V1 V2 V3 V4 V5
0 0 10 0 30 100
0 0 5 0 0 0
0 0 0 50 0 0
0 0 0 0 0 10
0 0 0 20 0 60
0 0 0 0 0 0
V0
输出样例1
0-1-5----[0 1 ]
0-2-9----[0 3 2 ]
0-3-7----[0 3 ]
0-4-10----[0 3 2 4 ]
V0-V1–1
V0-V2-10----[V0 V2 ]
V0-V3-50----[V0 V4 V3 ]
V0-V4-30----[V0 V4 ]
V0-V5-60----[V0 V4 V3 V5 ]
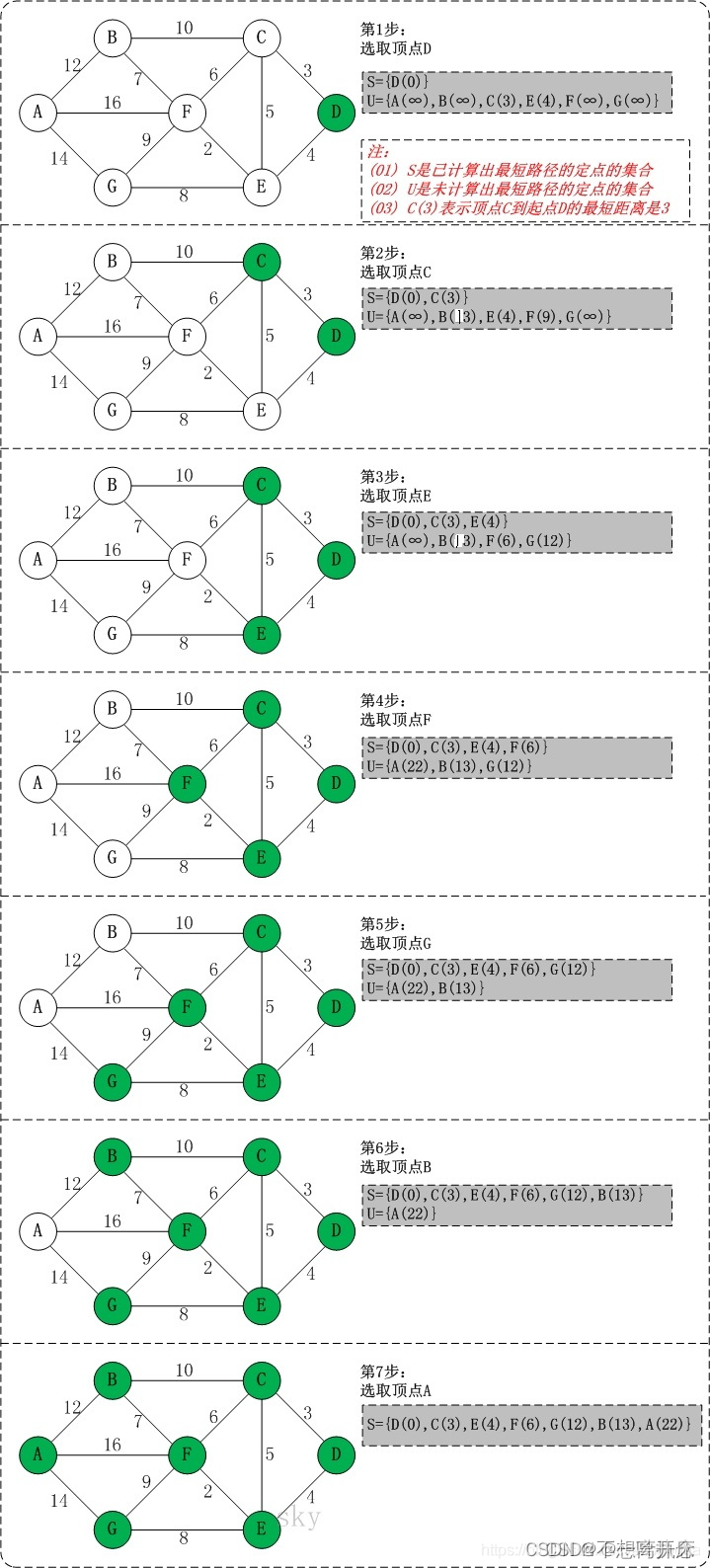
Dijkstra算法
思路
- 取一个点,称为原点,求该点到其他所有点的最短路径。
- 先取一个点在集合中,比较该点到其他任意一个点的最短路径
- 将该点加入集合,更新原点到不在集合中的点的路径是否可以更换为经过新加的点再到该点,如!果更短就更换,再重复这个过程
#include<bits/stdc++.h>
using namespace std;
int main()
{int t;cin>>t;for(int i = 0; i < t; i++){int n;cin>>n;//记录节点string s[205];//记录路径 不记录起点和终点string arr[205] = {""};//记录节点所在下标map<string,int> m;for(int j = 0; j < n; j++) {cin>>s[j];m[s[j]] = j;}//邻接矩阵int a[205][205] = {0};for(int j = 0; j < n; j++){for(int k = 0; k < n; k++) cin>>a[j][k];}string v;cin>>v;int start = m[v];//记录是否加入集合中,即是否已计算最短路径int visited[205] = {0};visited[start] = 1;while(1){//找到最短路径并记录int flag = -1;int small = 99999999;for(int j = 0; j < n; j++){if(!visited[j] && a[start][j] && a[start][j] < small){small = a[start][j];flag = j;}}//全部找完 退出if(flag == -1) break;visited[flag] = 1;//更新经过新加的点的最短路径for(int j = 0; j < n; j++){if(!visited[j] && a[flag][j] && (a[start][j] == 0 || a[start][j] > a[start][flag] + a[flag][j])){a[start][j] = a[start][flag] + a[flag][j];//路径记录arr[j] = arr[flag] + s[flag] + " ";}}}for(int j = 0; j < n; j++){if(j != start){if(a[start][j]) {if(arr[j] == "") printf("%s-%s-%d----[%s %s ]\n",v.c_str(),s[j].c_str(),a[start][j],v.c_str(),s[j].c_str());else printf("%s-%s-%d----[%s %s%s ]\n",v.c_str(),s[j].c_str(),a[start][j],v.c_str(),arr[j].c_str(),s[j].c_str());}else printf("%s-%s--1\n",v.c_str(),s[j].c_str());}}}return 0;
}