Top-K问题是在海量数据中找到最大或最小的K个元素,它在实际应用中非常常见,例如专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。在面对大规模数据时,直接对数据进行排序可能效率低下,因为排序的时间复杂度通常为O(n log n),而海量数据可能无法完全加载到内存中。因此,我们需要一种更高效的算法来解决Top-K问题
用堆解决Top-K问题
堆排序是一种高效的解决Top-K问题的方法。基本思路如下:
-
用数据集合中前K个元素来建堆。对于前K个最大的元素,我们建立一个小堆;对于前K个最小的元素,我们建立一个大堆。
-
用剩余的N-K个元素依次与堆顶元素来比较,如果大于(或小于)堆顶元素,则替换堆顶元素,并进行堆调整。
通过这个过程,堆中剩余的K个元素就是所求的前K个最小或最大的元素
void PrintTopK(int* a, int n, int k)
{// 1. 建堆--用a中前k个元素建堆// 2. 将剩余n-k个元素依次与堆顶元素交换,不满则则替换
}
void TestTopk()
{int n = 10000;int* a = (int*)malloc(sizeof(int)*n);srand(time(0));for (size_t i = 0; i < n; ++i){a[i] = rand() % 1000000;}a[5] = 1000000 + 1;a[1231] = 1000000 + 2;a[531] = 1000000 + 3;a[5121] = 1000000 + 4;a[115] = 1000000 + 5;a[2335] = 1000000 + 6;a[9999] = 1000000 + 7;a[76] = 1000000 + 8;a[423] = 1000000 + 9;a[3144] = 1000000 + 10;PrintTopK(a, n, 10);
}对随机位置改10个值 如果能选出这10个 就说明代码没问题
假设有10亿个值 这时让你取前10 那我们选择建立一个10个数据大小的堆
我们读写整形用fscanf 和fprintf
这时我们创建一个函数将其写入文档
void CreateNode()
{int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin= fopen(file, "w");if (fin == NULL){perror("fopen fail");return;}for (int i = 0; i < n; ++i){int x = (rand() + i) % 10000000;//+i是为了减少重复值 因为rand最多就三万个随机值 fprintf(fin, "%d\n", x);}
}
此时文件已经被创建成功
接下来实现打印Top k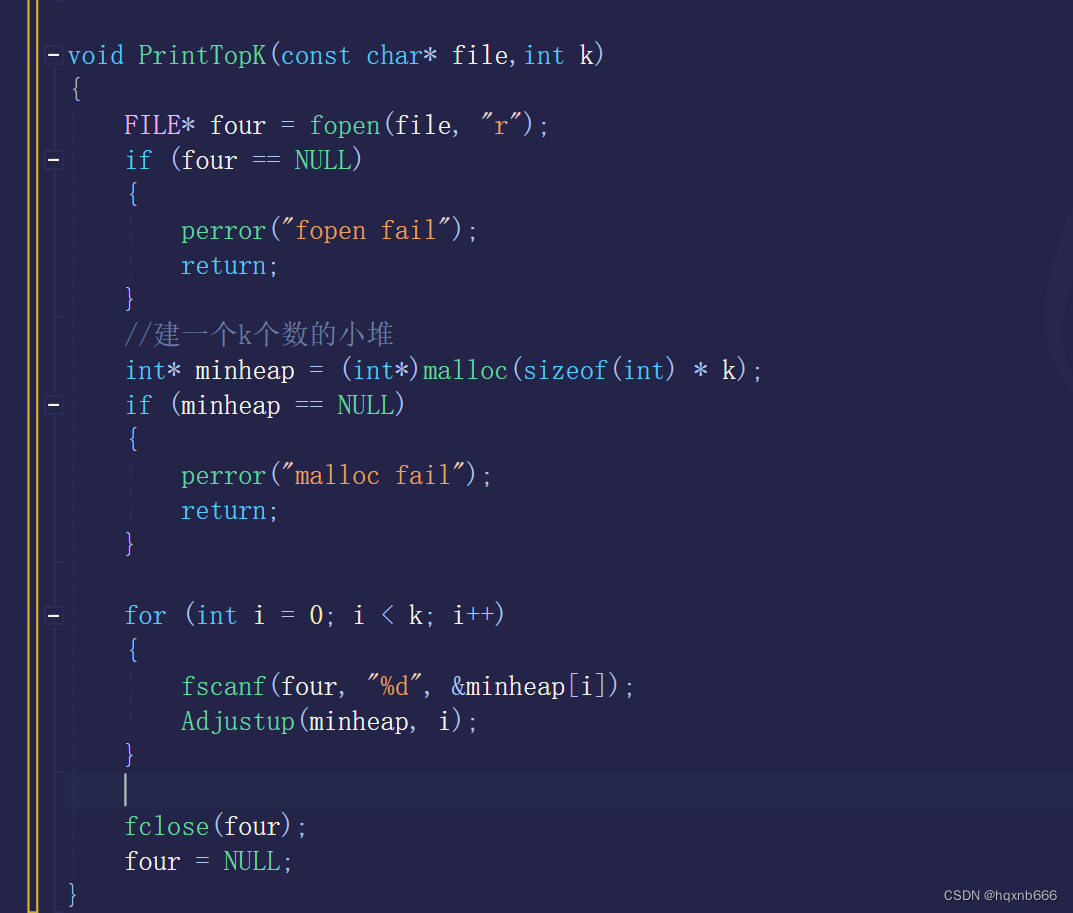
在这里我们创建了一个小堆 由于fscanf的返回值是当读取结束时返回EOF

所以我们可以创造循环

然后我们填写测试用例

通过调试我们可以看到他的逻辑过程

最后得出结果
实现代码
以下是一个简单的C语言代码示例,展示了如何使用小堆解决Top-K问题:
#include <stdio.h>
#include <stdlib.h>
#include <time.h>// 堆数据结构
typedef struct {int* a; // 存放堆元素的数组int capacity; // 数组容量int size; // 当前堆的大小
} HP;// 交换两个元素的值
void Swap(int* p1, int* p2) {int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// 向上调整(建堆时使用)
void Adjustup(int* a, int child) {int parent = (child - 1) / 2;while (child > 0 && a[child] < a[parent]) {Swap(&a[child], &a[parent]);child = parent;parent = (parent - 1) / 2;}
}// 向下调整(堆调整时使用)
void Adjustdown(int* a, int size, int parent) {int child = parent * 2 + 1;while (child < size) {if (child + 1 < size && a[child + 1] < a[child]) {++child;}if (a[child] < a[parent]) {Swap(&a[child], &a[parent]);parent = child;child = (child + 1) * 2;} else {break;}}
}// 初始化堆
void HPInit(HP* php, int capacity) {php->a = (int*)malloc(sizeof(int) * capacity);php->capacity = capacity;php->size = 0;
}// 销毁堆
void HPDestory(HP* php) {free(php->a);php->a = NULL;php->capacity = 0;php->size = 0;
}// 入堆操作
void HPPush(HP* php, int x) {if (php->size == php->capacity) {// 堆满时,扩容int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;int* tmp = (int*)realloc(php->a, sizeof(int) * newcapacity);if (tmp == NULL) {perror("realloc fail");return;}php->a = tmp;php->capacity = newcapacity;}php->a[php->size] = x;php->size++;Adjustup(php->a, php->size - 1);
}// 出堆操作
int HPPop(HP* php) {if (php->size == 0) {perror("Heap is empty");return -1; // 堆为空}int top = php->a[0];php->a[0] = php->a[php->size - 1];php->size--;Adjustdown(php->a, php->size, 0);return top;
}// 获取堆顶元素
int HPTop(const HP* php) {if (php->size == 0) {perror("Heap is empty");return -1; // 堆为空}return php->a[0];
}// 打印前K个最小元素
void PrintTopK(const char* file, int k) {FILE* fin = fopen(file, "r");if (fin == NULL) {perror("fopen fail");return;}// 建立一个大小为k的小堆HP minheap;HPInit(&minheap, k);int x = 0;// 读取文件中的元素并插入堆while (fscanf(fin, "%d", &x) != EOF) {if (minheap.size < k) {// 如果堆的大小小于k,直接插入HPPush(&minheap, x);} else if (x > HPTop(&minheap)) {// 否则,如果当前元素比堆顶元素大,替换堆顶元素并调整堆HPPop(&minheap);HPPush(&minheap, x);}}// 输出结果for (int i = 0; i < k; i++) {printf("%d ", HPPop(&minheap));}printf("\n");fclose(fin);HPDestory(&minheap);
}// 生成随机数据文件
void CreateNode() {int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL) {perror("fopen fail");return;}for (int i = 0; i < n; ++i) {int x = (rand() + i) % 10000000;fprintf(fin, "%d\n", x);}fclose