分享金蝶云星空跟泛微OA系统集成对接的方案分享,主讲审批流程对接,表单对接的两类场景。分别是金蝶云星空发起申请和泛微发起流程审批,最终实现统一管理。

数据集成主要有以下好处:
(1)数据一致性:通过数据集成,聚水潭和金蝶云星空的数据可以实现一致性。
(2)功能互补:聚水潭和金蝶云星空分别承担着不同的职能,数据集成可以实现功能的互补。
(3)提升效率:数据集成可以减少人工的重复操作,提升工作效率。
(4)实时更新:通过数据集成,系统之间的数据可以实时更新。
一、由泛微发起审批同步到金蝶云星空做单处理
描述:审批流程整合,金蝶云星空和泛微OA可以对接审批流程,实现跨系统的流程整合。例如,当在泛微OA中发起一个审批流程时,可以将相关数据传输到金蝶云星空的审批模块进行后续处理。这样,企业可以在不同系统之间无缝衔接,提高审批效率。
同步条件:泛微必须审批通过,按审批 通过后的数据进行同步成方案。
应用场景:报销单,收付款单,入职申请等流程。

二、由金蝶云星空发起审批同步到泛微OA审批
描述:金蝶云星空和泛微OA的对接可以使得数据报表的生成和分析更加便捷。例如,金蝶云星空可以通过对接泛微OA获取相关的数据,然后进行数据分析和报表生成,为企业提供决策支持。
同步条件:此方案同步涉及到基础资料,需要将金蝶云星空物料,客户,供应商等同步至泛微OA。
应用场景:采购合同,销售合同,采购申请单等表单。

三、数据流转流程
对接应用场景,双方调用接口示例:
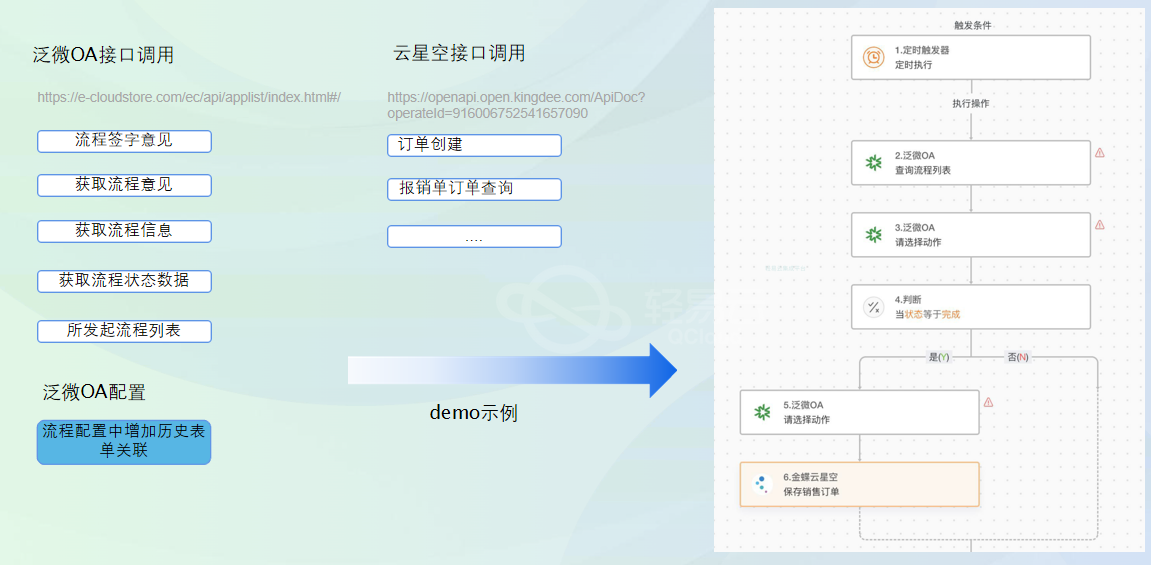
总结
以上对接方案是金蝶云星空对接泛微OA常见的两类场景,对接过程中会涉及到很多基础资料集成的问题,例:人员,部门,组织,物料,客户,科目,费用,币别,多语言等这块的内容会涉及到写库的一些操作。
通过金蝶云星空和泛微OA的对接,企业可以实现不同系统之间的数据同步和流程整合,提高工作效率和管理效果。这种集成方案不仅适用于中小型企业,也适用于大型企业的复杂业务场景。
关于具体的对接详情可以给我留言。