数据结构实验十二 图的遍历及应用

一、【实验目的】

1、 理解图的存储结构与基本操作；
2、熟悉图的深度度优先遍历和广度优先遍历算法
3、掌握图的单源最短路径算法

二、【实验内容】

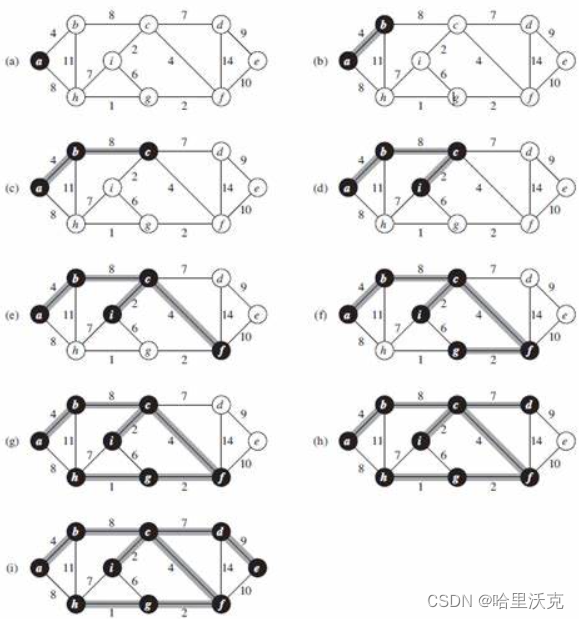
1.根据下图邻接矩阵，编程实现该图的深度与广度优先遍历算法，输出遍历序列。

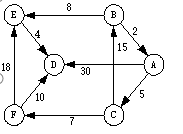
2.单源节点最短路径问题
问题描述:求从有向图的某一结点出发到其余各结点的最短路径。
基本要求:
（1）有向图采用邻接矩阵表示。
（2）单源节点最短路径问题采用Dijkstra算法。
（3）输出有向图中从源结点T到其余各结点的最短路径和最短路径值。

三、实验源代码

🍻 CPP

#include<iostream>
#include<queue>
#include<cstring>
#include<vector>
using namespace std;const int N = 6;
const int M = N*N;
const int INF = 0x3f3f3f3f;
const int 无边 = -1;int g[N][N]; //grap数组记录邻接矩阵【-1 表示不可达】
bool vs[N];//visted数组记录结点是否已经被访问过void add(int a, int b, int c)
{// 邻接矩阵加边g[a][b] = c;
}void init()
{for(int i = 0; i < N; i++)for(int j = 0; j < N; j++)g[i][j] = 无边;//初始化为不可达状态【-1】// A B C D E F// 0 1 2 3 4 5// 加边add(1, 0, 2);add(2, 1, 15);add(0, 2, 5);add(0, 3, 30);add(2, 5, 7);add(1, 4, 8);add(4, 3, 4);add(5, 3, 10);add(5, 4, 18);
}void print()
{// 输出邻接矩阵cout << "输出邻接矩阵:" << endl;cout << "   A  B  C  D  E  F" << endl;char c = 'A';for (int i = 0; i < N; i++){cout << c++ << "  ";for (int j = 0; j < N; j++)printf("%-2d ",g[i][j]);
//          cout << g[i][j] << " ";cout << endl;}
}//深度优先遍历
// u 是当前访问的点
void dfs(int u)
{cout << char(u+'A') << " " ;vs[u] = true;//标记以访问for(int i = 0; i < N; i++)//访问当前结点可达的结点（有边）{int e = g[u][i];if(vs[i])//已访问过continue;if(e == 无边)//无边continue;dfs(i);		}
}//广度优先遍历
// u 是当前访问的点
void bfs(int u)
{memset(vs,false,sizeof(vs));//初始化访问表为 未访问状态vs[u] = true;queue<int> q;//队列（先进先出）q.push(u);while(!q.empty()){int t = q.front();//取队头cout << char(t+'A') << " " ;q.pop();//队头出列for(int i = 0; i < N; i++)//访问当前结点可达的结点（有边）{int e = g[t][i];if(vs[i])//已访问过continue;if(e == 无边)//无边continue;q.push(i);vs[i] = true;}}
}int dist[N];//距离数组
int pre[N];//pre[i] 记录最短路径上，点 i 的前一个结点
//输出路径
void printRoute(int x)
{cout << "\nA到" << char(x + 'A') << "的最短路径长度为： " << dist[x] << endl;cout << "最短路径途径节点：";vector<int> v;while(x != -1){v.push_back(x);x = pre[x];}for(int i = v.size()-1; i >= 0; i--)cout << char(v[i]+'A') << " " ;cout << endl;
}//单源最短路 Dijkstra算法
void dijkstra(int u)//u表示起点
{cout << "\n\nDijkstra算法求最短路径"<<endl;memset(vs,false,sizeof(vs));//初始化访问表为 未访问状态memset(dist,0x3f,sizeof(dist));//初始化距离表为 无穷大memset(pre,-1,sizeof(pre));//初始化所有结点的前一个节点为 -1dist[u] = 0;for(int i = 0; i < N; i++){int t = -1;for(int j = 0; j < N; j++)//找n次{if(!vs[j] && (t == -1 || dist[j] < dist[t]))//循环找当前最小距离的点t = j;}printRoute(t);vs[t] = true;for(int j = 0; j < N; j++)//用当前最小距离的点尝试去更新其他点的距离{if(g[t][j] == 无边)continue;if(dist[j] > dist[t] + g[t][j]){dist[j] = dist[t] + g[t][j];pre[j] = t;//记录前驱节点}}	}	
}
int main()
{init(); // 初始化图print(); // 输出邻接矩阵和邻接表cout<< "\n深度优先遍历：";memset(vs,false,sizeof(vs));//初始化访问表为 未访问状态dfs(0);cout<< "\n广度优先遍历：";bfs(0);dijkstra(0);return 0;
}

🍻 C

#include<stdio.h>
#include<string.h>
#include<limits.h>
#include<stdbool.h>#define N 6
#define M (N * N)
#define INF 0x3f3f3f3f
#define NO_EDGE -1int g[N][N]; // graph数组记录邻接矩阵【-1 表示不可达】
bool vs[N]; // visited数组记录结点是否已经被访问过void add(int a, int b, int c)
{// 邻接矩阵加边g[a][b] = c;
}void init()
{for (int i = 0; i < N; i++){for (int j = 0; j < N; j++){g[i][j] = NO_EDGE; // 初始化为不可达状态【-1】}}// A B C D E F// 0 1 2 3 4 5// 加边add(1, 0, 2);add(2, 1, 15);add(0, 2, 5);add(0, 3, 30);add(2, 5, 7);add(1, 4, 8);add(4, 3, 4);add(5, 3, 10);add(5, 4, 18);
}void print()
{// 输出邻接矩阵printf("输出邻接矩阵:\n");printf("   A  B  C  D  E  F\n");char c = 'A';for (int i = 0; i < N; i++){printf("%c  ", c++);for (int j = 0; j < N; j++){if (g[i][j] == NO_EDGE){printf(" - ");}else{printf("%-2d ", g[i][j]);}}printf("\n");}
}//深度优先遍历
// u 是当前访问的点
void dfs(int u)
{printf("%c ", u + 'A');vs[u] = true; // 标记已访问for (int i = 0; i < N; i++) // 访问当前结点可达的结点（有边）{int e = g[u][i];if (vs[i]) // 已访问过continue;if (e == NO_EDGE) // 无边continue;dfs(i);}
}//广度优先遍历
// u 是当前访问的点
void bfs(int u)
{memset(vs, false, sizeof(vs)); // 初始化访问表为未访问状态vs[u] = true;printf("%c ", u + 'A');int queue[N];int front = 0, rear = 0;queue[rear++] = u;while (front != rear){int t = queue[front++];for (int i = 0; i < N; i++) //访问当前结点可达的结点（有边）{int e = g[t][i];if (vs[i]) //已访问过continue;if (e == NO_EDGE) //无边continue;printf("%c ", i + 'A');queue[rear++] = i;vs[i] = true;}}
}int dist[N];   //距离数组
int pre[N];    //pre[i] 记录最短路径上，点 i 的前一个结点//输出路径
void printRoute(int x)
{printf("\nA到%c的最短路径长度为：%d\n", x + 'A', dist[x]);printf("最短路径途径节点：");int v[N], cnt = 0;while (x != -1){v[cnt++] = x;x = pre[x];}for (int i = cnt - 1; i >= 0; i--){printf("%c ", v[i] + 'A');}printf("\n");
}//单源最短路 Dijkstra算法
void dijkstra(int u) //u表示起点
{printf("\n\nDijkstra算法求最短路径\n");memset(vs, false, sizeof(vs));   //初始化访问表为未访问状态memset(dist, INF, sizeof(dist)); //初始化距离表为无穷大memset(pre, -1, sizeof(pre));    //初始化所有结点的前一个节点为-1dist[u] = 0;for (int i = 0; i < N; i++){int t = -1;for (int j = 0; j < N; j++) //找n次{if (!vs[j] && (t == -1 || dist[j] < dist[t])) //循环找当前最小距离的点t = j;}printRoute(t);vs[t] = true;for (int j = 0; j < N; j++) //用当前最小距离的点尝试去更新其他点的距离{if (g[t][j] == NO_EDGE)continue;if (dist[j] > dist[t] + g[t][j]){dist[j] = dist[t] + g[t][j];pre[j] = t; //记录前驱节点}}}
}int main()
{init();  // 初始化图print(); // 输出邻接矩阵和邻接表printf("\n深度优先遍历：");memset(vs, false, sizeof(vs)); //初始化访问表为未访问状态dfs(0);printf("\n广度优先遍历：");bfs(0);dijkstra(0);return 0;
}