创作目的：为了方便自己后续复习重点，以及养成写博客的习惯。

一、找树左下角的值

思路：采用递归

ledcode题目：https://leetcode.cn/problems/find-bottom-left-tree-value/description/

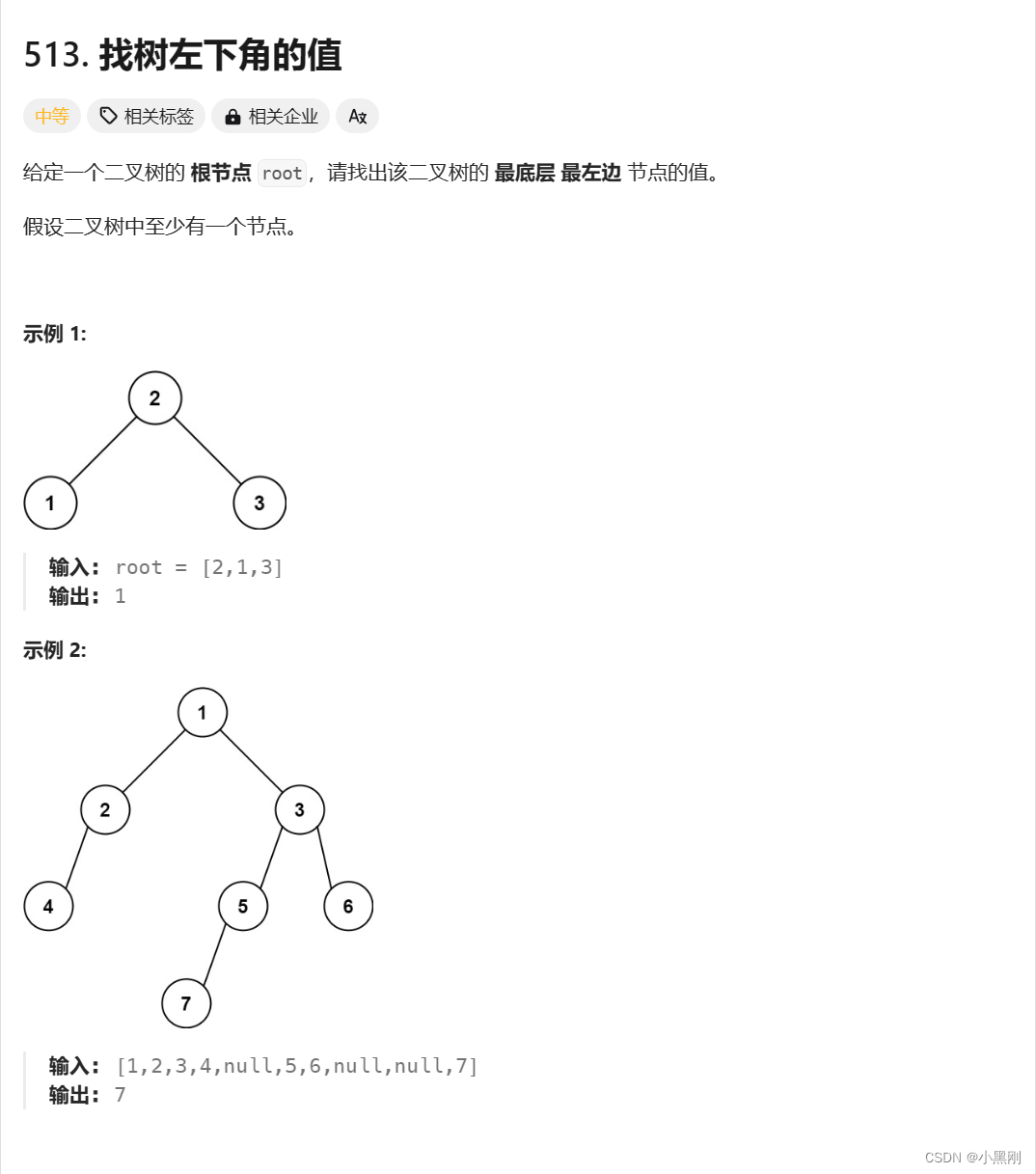
AC代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/void dfs(const struct TreeNode *root ,int height, int *curVal ,int *curHeight) {if(root == NULL) {return ;}height++;dfs(root->left,height,curVal,curHeight);dfs(root->right,height,curVal,curHeight);if(height > *curHeight) {*curHeight = height;*curVal    = root->val;}}
int findBottomLeftValue(struct TreeNode* root) {int curVal,curHeight = 0;dfs(root,0,&curVal,&curHeight);return curVal;
}

二、路径总和

思路：采用递归，判断targetSum == root->val，sum的值每次更新减去前一个val即可。

lecode题目：https://leetcode.cn/problems/path-sum/

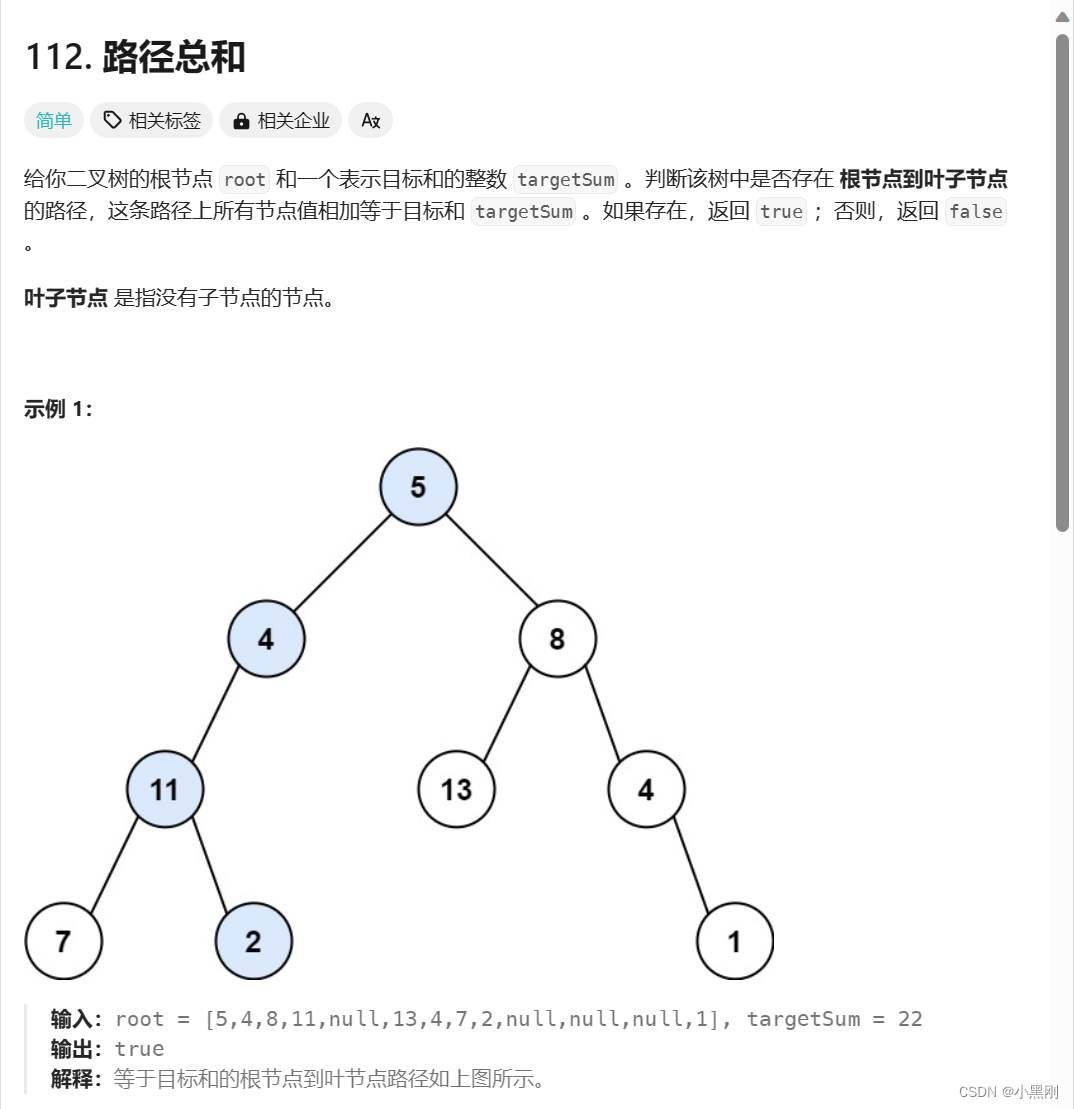
AC代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/
bool hasPathSum(struct TreeNode* root, int targetSum) {if(root == NULL) {return false;}if(root->left == NULL && root->right == NULL) {return targetSum == root->val;}return hasPathSum(root->left,targetSum - root->val) || hasPathSum(root->right,targetSum - root->val);
}

三、从中序与后序遍历序列构造二叉树

思路：采用迭代的方法，代码参考的是ledcode题解

ledcode题目：https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/

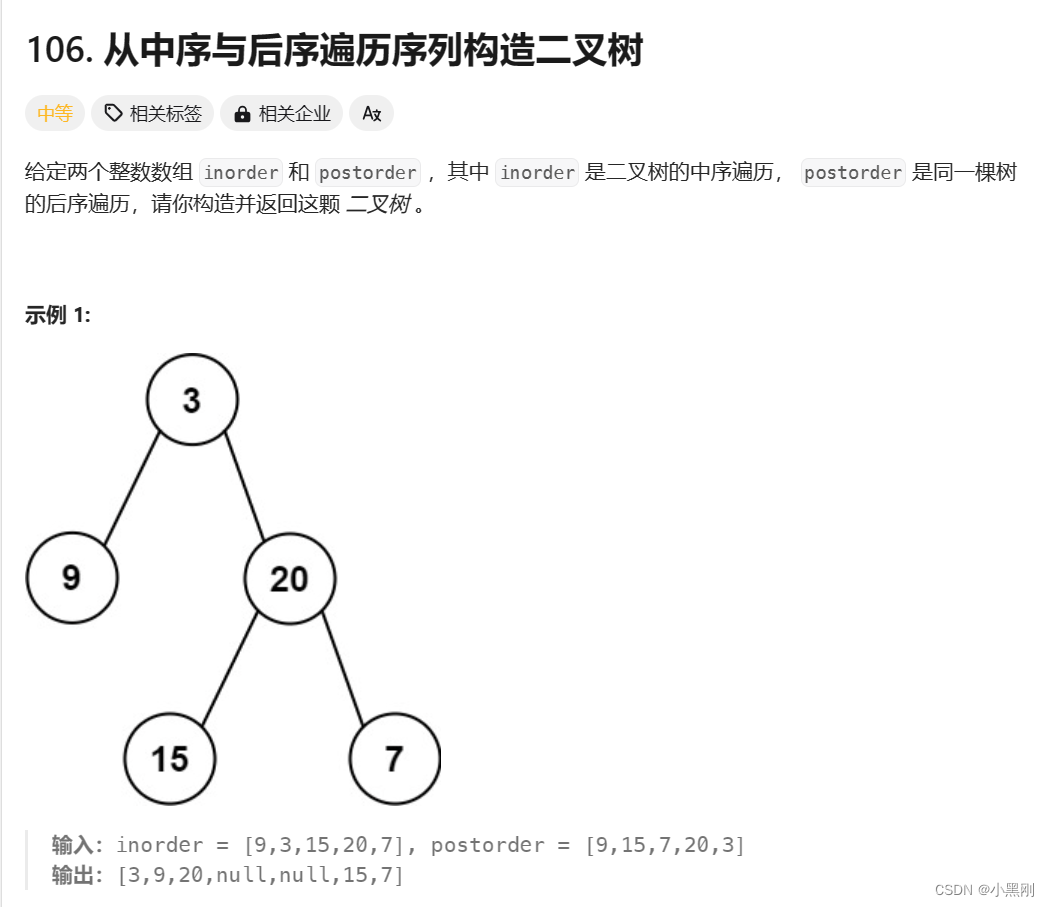
AC代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     struct TreeNode *left;*     struct TreeNode *right;* };*/struct TreeNode* createTreeNode(int val) {struct TreeNode* ret = malloc(sizeof(struct TreeNode));ret->val = val;ret->left = ret->right = NULL;return ret;}
struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize) {if(postorderSize == 0) {return NULL;}struct TreeNode* root = createTreeNode(postorder[postorderSize - 1]);struct TreeNode** s = malloc(sizeof(struct TreeNode*)* 10001);int top = 0;s[top++] = root;int inorderIndex = inorderSize - 1;for(int i = postorderSize - 2;i >= 0;i--) {int postorderVal = postorder[i];struct TreeNode* node = s[top - 1];if(node->val != inorder[inorderIndex]) {node->right = createTreeNode(postorderVal);s[top++] = node->right;}else {while(top > 0 && s[top - 1]->val == inorder[inorderIndex]) {node = s[--top];inorderIndex--;}node->left = createTreeNode(postorderVal);s[top++] = node->left;}}return root;
}

全篇后记：

虽然难度在不断增加，但坚持下去总会有收获。