题目1:1049 最后一块石头的重量
题目链接:最后一块石头的重量
对题目的理解
整数数组stone[i]表示第i块石头的重量,每次从中选出任意两块石头(x<=y)粉碎
如果两块石头重量相等,就会被完全粉碎;如果不等,那么重量轻(x)的石头会被粉碎,另一块石头重量变为y-x
每次最多剩下一块石头,返回此石头可能的最小重量,如果没有石头剩下,就返回0
stone数组中的元素在1~100之间,数组长度在1~30之间
每次让数值相近的石头一起粉碎,这样最终得到的重量会减少,本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
本题物品的重量是stones[i],物品的价值也是stones[i]
动规五部曲
1)dp数组的含义及下标i的含义
dp[j]:表示背包容量为j背的最大价值,
本题表示背包中容量是j时,最大重量是dp[j]
2)递推公式
01背包:dp[j]=max(dp[j],dp[j-weight[i]]+value[i])
dp[j]=max(dp[j],dp[j-stones[i]]+stones[i])
3)dp数组初始化
dp[0]=0 ,根据递推公式,非零下标对应的dp[j]也初始化为0,这样才不会覆盖初始值
1 <= stones.length <= 30,1 <= stones[i] <= 100,所以最大重量就是30 * 100 ,但是背包只需要装最大重量的一半即可(因为将石头分成重量相等的两堆),target=sum/2=3000/2=1500
4)遍历顺序
先正序遍历物品,后倒序遍历背包
for(i=0;i<stones.size();i++){
for(j=target;j>=stones[i];j--)}
5)打印dp数组
最后dp[target]里是容量为target的背包所能背的最大重量,那么分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target],
因为target=sum/2,是直接抹去小数部分,所以sum-dp[target]>=target
最终石头的最小重量是result=(sum-dp[target])-dp[target]
代码
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {//数组长度最大是30,数组中的元素最大是100,所以dp数组承受的最大重量是30*100=3000,分成重量相同的两堆,所以大小是1500+1//dp数组初始化vector<int> dp(1501,0);int sum = 0;for(int i=0;i<stones.size();i++){sum += stones[i];}int target = sum/2;//递推,先正序遍历物品,后倒序遍历背包for(int i=0;i<stones.size();i++){for(int j=target;j>=stones[i];j--){dp[j]=max(dp[j],dp[j-stones[i]]+stones[i]);}}int result = sum-dp[target]-dp[target];return result;}
};- 时间复杂度:O(m × n) , m是石头总重量(准确的说是总重量的一半),n为石头块数
- 空间复杂度:O(m)
题目2:494 目标和
题目链接:目标和
对题目的理解
非负整数数组的每个数字前添加 '+' 或 '-' 得到表达式,计算表达式运算结果等于target的不同表达式的数目
本题还是分成两个部分,加法集合left 减法集合right,这两个集合满足下面的两个等式①②
① left+right=sum
② left-right=target
right=sum-left
left-(sum-left)=target-->2left-sum=taget left=(target+sum)/2 注:只有能整除才能找到
如果不能整除,则不存在这样的元素组合使得运算结果等于target,
如果target的绝对值的大于sum,也是无解的
背包容量是left时,看元素中有多少种方式能够装满这个背包,每个元素只用1次,是01背包问题
动规五部曲
1)dp[j]数组即下标j的含义
背包容量为j时,装满背包有dp[j]种方法
2)递推公式

递推公式:dp[j] += dp[j-nums[i]] ,在后面在讲解背包解决排列组合问题的时候还会用到!
3)dp数组初始化
dp[0]=1,如果数组[0] ,target = 0,那么 left = (target + sum) / 2 = 0, dp[0]也应该是1, 也就是说给数组里的元素 0 前面无论放加法还是减法,都是 1 种方法。
根据递推公式 因为递推公式是累加的,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。,所以非零下标的dp[j]初始为0
4)遍历顺序
01背包:正序遍历物品(元素),倒序遍历背包(left)
5)打印dp数组
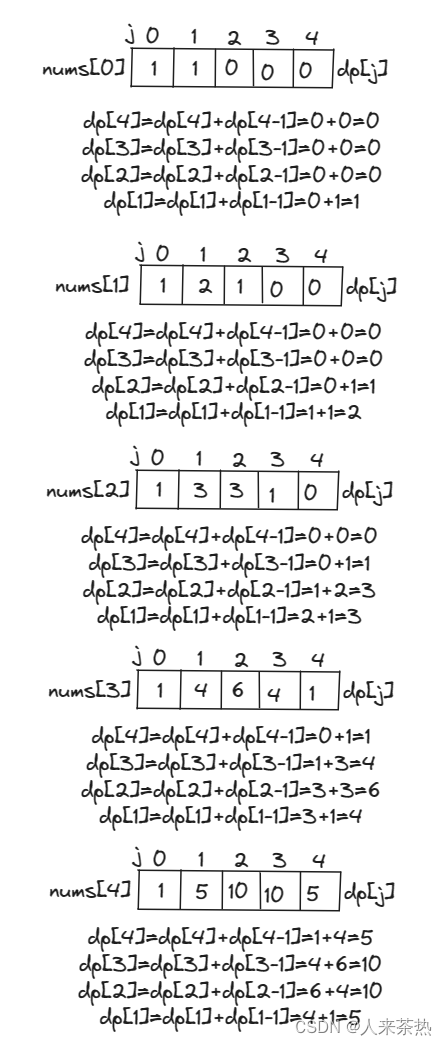
代码
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum=0;for(int i=0;i<nums.size();i++){sum += nums[i];}int left = (target+sum)/2;//dp数组里面尽可能地装left容量 -500~1000if((target+sum)%2==1) return 0;if(abs(target)>sum) return 0;//初始化dp数组vector<int> dp(left+1,0);dp[0]=1;//递推for(int i=0;i<nums.size();i++){for(int j=left;j>=nums[i];j--){dp[j] += dp[j-nums[i]];}}return dp[left];}
};- 时间复杂度:O(n × m),n为正数个数,m为背包容量
- 空间复杂度:O(m),m为背包容量
本题记住:求装满背包有几种方法,递推公式为
dp[j] += dp[j-nums[i]];题目3:474一和零
题目链接:一和零
对题目的理解
返回二进制字符串数组strs最大子集长度,该子集中最多有m个0和n个1,二进制字符串仅由0,1组成
题目要求:strs字符串数组中至少有1个字符串,最多有600个字符串;每个字符串的长度至少为1,最多是100
背包有两个维度,m个0和n个1,装满这个背包有多少个物品
不同长度的字符串就是不同大小的待装物品,每个物品只能使用1次,所以是01背包问题
动规五部曲
1)dp数组及下标i的含义
二维dp数组,dp[i][j] 装满i个0,j个1的背包最多背了dp[i][j]个物品
2)递推公式
01背包递推公式:dp[j]=max(dp[j],dp[j-weight[i]]+value[i])
每个物品的重量是x个0,y个1,是两个维度,所以递推公式为dp[i][j]=max(dp[i][j], dp[i-x][j-y]+1)
3)dp数组初始化
dp[0][0]=0 非零下标 ,若初始化为一个较大的正整数,那么根据递推公式,值会被覆盖掉
所以非零下标的dp[j]也初始化为非负整数的最小值,即0
4)遍历顺序
01背包:先正序遍历物品strs里的字符串,后倒序遍历背包(两个维度,m和n)
5)打印dp数组
代码
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {//定义并初始化dp数组,这个数组是一个二维数组,有这两个重量0和1vector<vector<int>> dp(m+1,vector<int>(n+1,0));//递推,先正序遍历物品,后倒序遍历背包for(string str:strs){//遍历物品(字符串数组)int x=0;//记录当前字符串中0的个数int y=0;//记录当前字符串中1的个数for(char c:str){//遍历字符串中的每个字符,统计字符串中0和1的数量if(c=='0') x++;else y++;} for(int i=m;i>=x;i--){//遍历背包for(int j=n;j>=y;j--){dp[i][j]=max(dp[i][j],dp[i-x][j-y]+1);}}}return dp[m][n];}
};- 时间复杂度: O(kmn),k 为strs的长度
- 空间复杂度: O(mn)