文章目录
- 二分
- 一、整数二分
- (一)整数二分思路
- (二)整数二分算法模板
- 1.左查找(寻找左侧边界)
- 2.右查找(寻找右侧边界)
- 3.总模板
- (三)题目:数的范围
- 二、浮点数二分
- (一)浮点数二分思路
- (二)浮点数二分算法模板
- (三)题目:数的三次方根
二分
一、整数二分
(一)整数二分思路
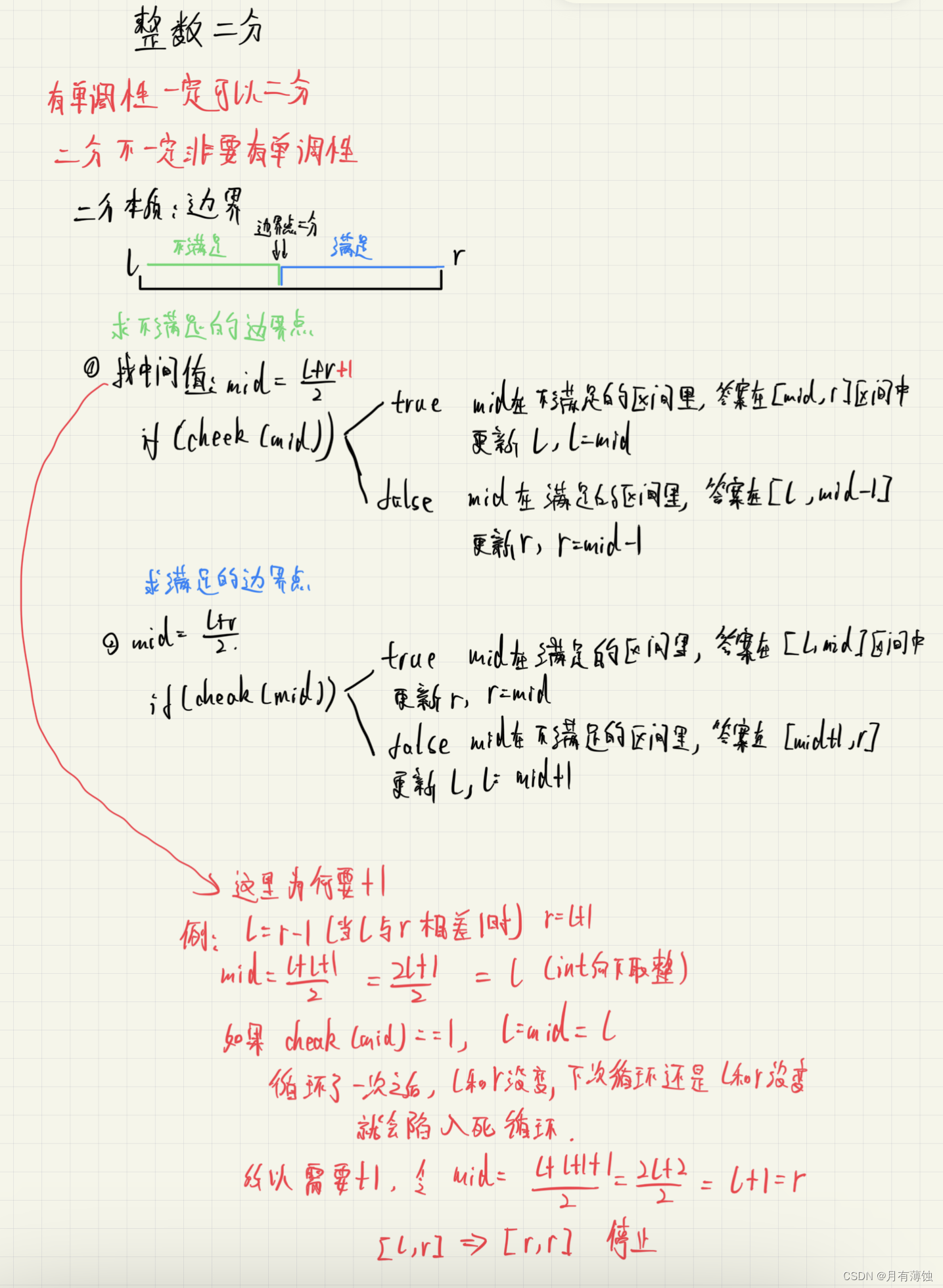
(二)整数二分算法模板
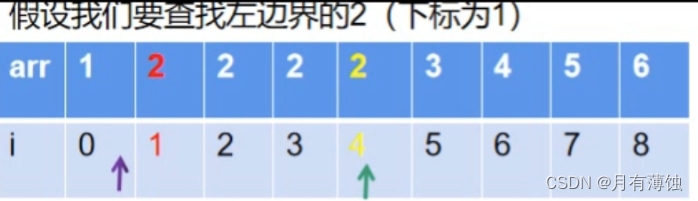
1.左查找(寻找左侧边界)
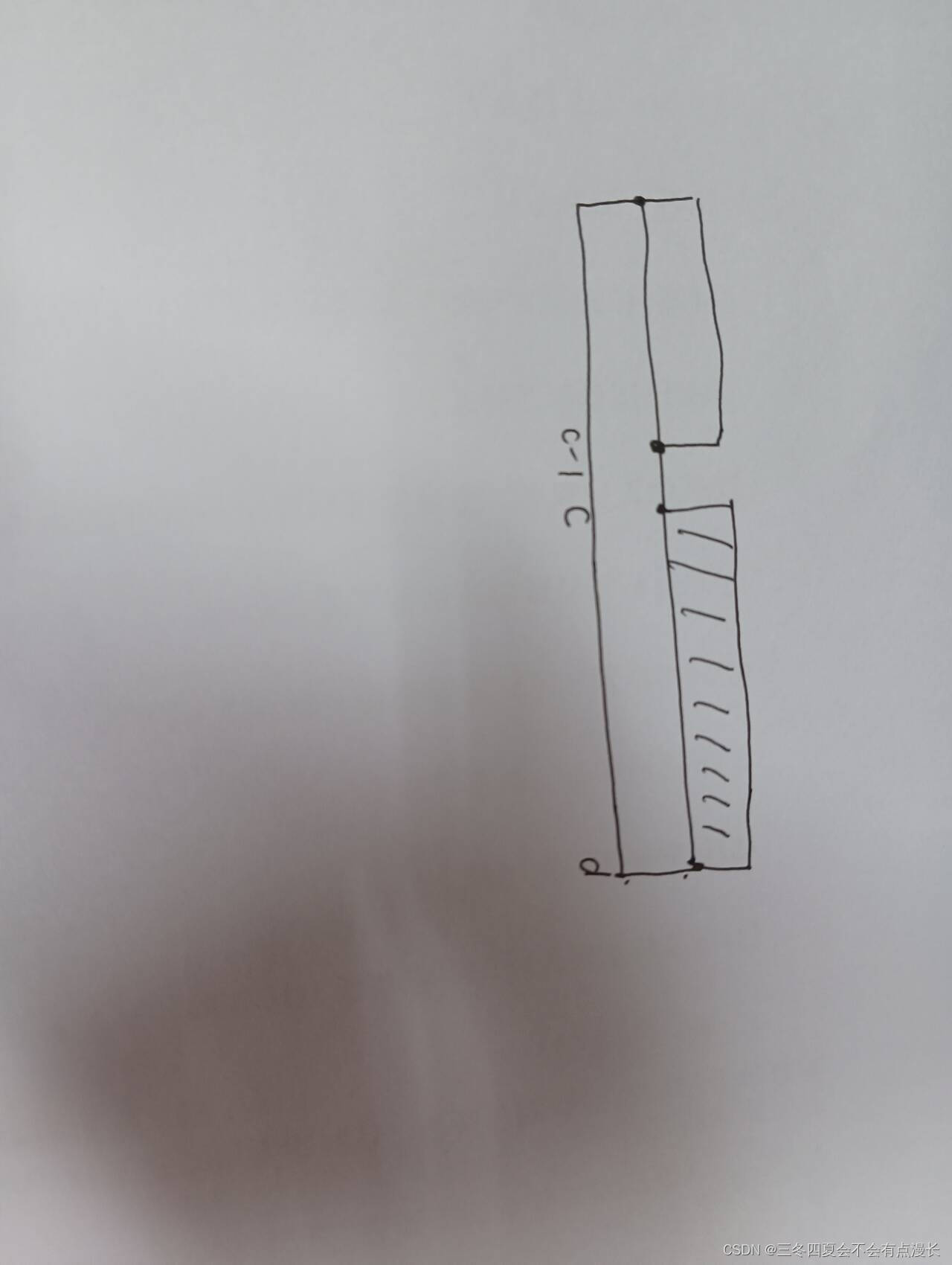
- 查找的情况分为三种:
- 当a[mid]>2时,r=mid-1,l不变
- 当a[mid]<2时,l=mid+1,r不变
- 当a[mid]==2时,如果我们一找到就返回,那么,返回的结果将会是下标4,此时并不是目标值
因此,我们需要向左缩小区间
-
向左缩小区间:就是令r=mid,l不变;此时区间变为[0,4],既保证了下标为4的2保留在区间里,又保证可以继续查找[0,4]中是否还有数字2,如果[0,3]中没有数字2了,则下标4就会是该区间唯一一个满足条件的值,也就会是最终结果。而如果[0,3]中还有其他的2,就如本例,那么下标为4的数字就会被下一次缩小区间所抛弃。
-
这里模拟一下样例:

最后l == r退出循环。此时如果r就是最终结果,那么l同时也是最终结果。另一种退出循环的方式就是l>r,l跑到r的右边,那么不管怎么说,l都不可能是最终目标。因此最后只用判断r是否是最终目标就好了。 -
判断r是否是x:如果退出循环后a[r]==x,说明找到了x,并且这个x是左边界的x;如果a[r]!=x,说明连x都找不到,返回-1;
-
结果如下:
void query_l(int a)
{int l=0,r=n-1;while(l<r){int mid=(l+r)/2;if(arr[mid]==a) r=mid;else if(arr[mid]>a) r=mid-1;else l=mid+1;}if(arr[l]==a) cout<<r<<" ";else cout<<-1<<" ";
}
我们可以将等于和大于的情况合二为一,因为不管怎样最终都是要判断r是否为目标值的。所以,升级后的代码如下。
void query_l(int a)
{int l=0,r=n-1;while(l<r){int mid=(l+r)/2;if(arr[mid]>=a) r=mid;else l=mid+1;}if(arr[l]==a) cout<<r<<" ";else cout<<-1<<" ";
}
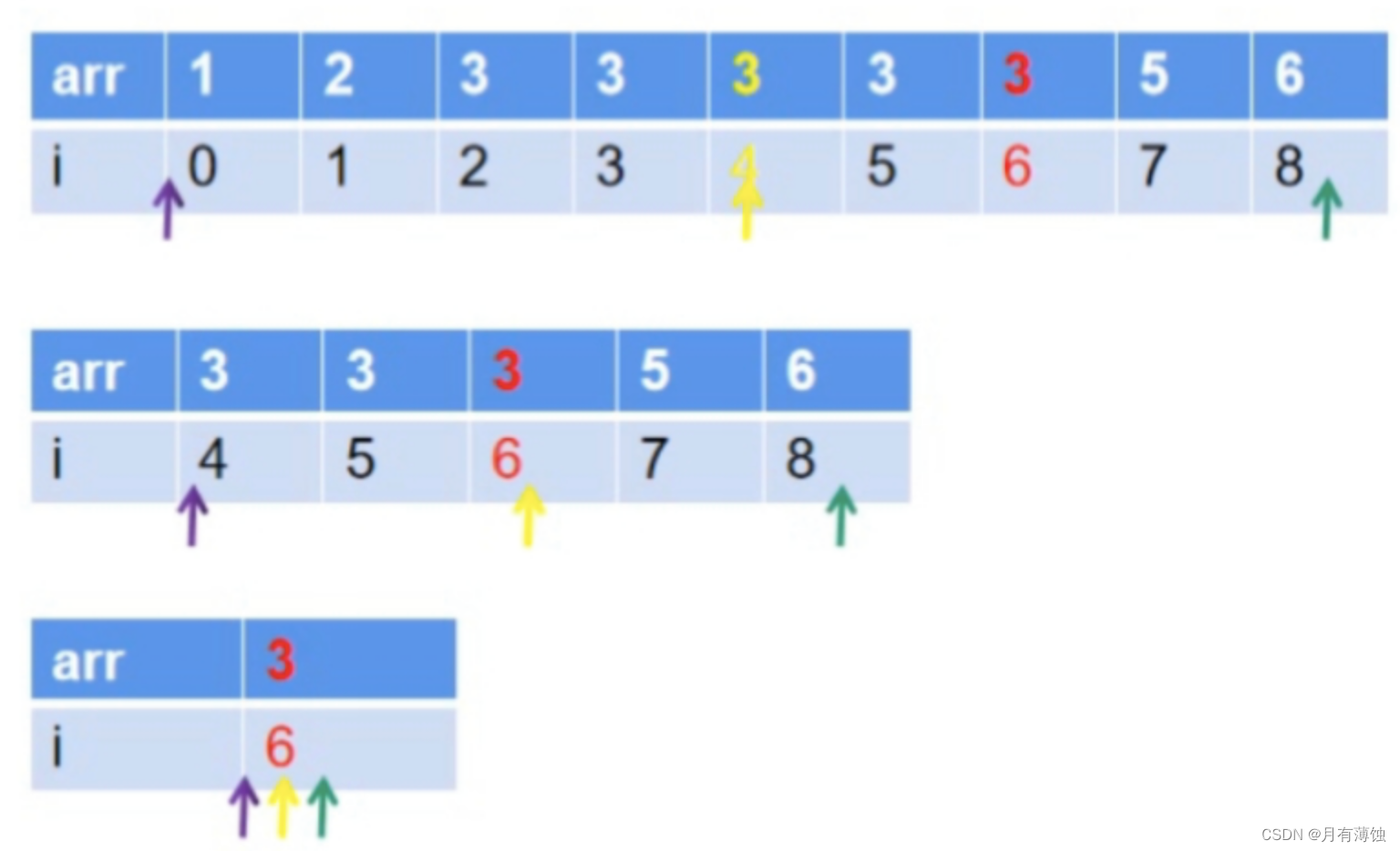
2.右查找(寻找右侧边界)
- 右查找就是要找到最后出现的值,不断向右缩小区间。分析过程与左查找类似。
- 需要注意的一点,右查找和左查找确定mid值的方式不同。左查找采用(l+r)/2向下取整的方式,右查找采用(l+r+1)/2向上取整的方式。
- 原因分析:
- 对于左查找:假设l=2,r=3,向下取整得到的mid=(2+3+1)/2=3,若取r=mid,那么l和r任保持原值不变,陷入死循环。
- 对于右查找:假设l=2,r=3,向下取整得到mid=(2+3)/2=2。若取l=mid,那么l和r任保持原值不变,陷入死循环。
void query_r(int a)
{int l=0,r=n-1;while(l<r){int mid=(l+r+1)/2;if(arr[mid]<=a) l=mid;else r=mid-1;}if(arr[r]==a) cout<<r;else cout<<-1;
}
3.总模板
bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (check(mid)) r = mid; // check()判断mid是否满足性质else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (check(mid)) l = mid;else r = mid - 1;}return l;
}
(三)题目:数的范围
给定一个按照升序排列的长度为 n的整数数组,以及 q个查询。对于每个查询,返回一个元素 k的起始位置和终止位置(位置从 0开始计数)。如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数 n和 q,表示数组长度和询问个数。
第二行包含 n个整数(均在 1∼10000范围内),表示完整数组。
接下来 q行,每行包含一个整数 k,表示一个询问元素。
输出格式
共 q行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤100000
1≤q≤10000
1≤k≤10000
输入样例:
6 3
1 2 2 3 3 4
3
4
5
输出样例:
3 4
5 5
-1 -1
#include<iostream>
using namespace std;
const int N = 100010;int n,m;
int q[N];int main()
{scanf("%d %d",&n,&m);for(int i=0;i<n;i++)scanf("%d",&q[i]);while(m--){int x;scanf("%d",&x);int l=0,r=n-1;while(l<r){int mid=(l+r)/2;if(q[mid]>=x)r=mid;else l=mid+1;}if(q[l]!=x)cout<<"-1 -1"<<endl;else{cout<<l<<" ";int l=0,r=n-1;while(l<r){int mid=(l+r+1)/2;if(q[mid]<=x)l=mid;elser=mid-1;}cout<<l<<endl;}}return 0;
}
二、浮点数二分
(一)浮点数二分思路
思路和整数二分一样,区别是浮点型二分不需要注意边界问题(也就是不需要+1)
(二)浮点数二分算法模板
bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r)
{const double eps = 1e-6; // eps 表示精度,取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}
(三)题目:数的三次方根
题目描述
给定一个浮点数n,求它的三次方根。
输入格式
共一行,包含一个浮点数n。
输出格式
共一行,包含一个浮点数,表示问题的解。
注意,结果保留6位小数。
数据范围
−10000≤n≤10000
输入样例:
1000.00
输出样例:
10.000000
#include<iostream>
using namespace std;
int main()
{double x;cin>>x;double l=-100,r=100;//根据题目范围 开三次方根 估计答案大概范围while(r-l>1e-8){double mid=(l+r)/2;if(mid*mid*mid>=x)r=mid;elsel=mid;}printf("%.6lf\n",l);return 0;
}