恋上数据结构与算法之二叉堆-编程知识

文章目录

- 需求分析
- Top K 问题
- 堆
- 堆的基本接口设计
- 二叉堆(Binary Heap)
- 最大堆
- - 添加
  - - 思路
    - 交换位置的优化
    - 实现
  - 删除
  - - 思路
    - 流程图解
    - 实现
  - replace
  - 批量建堆
  - - 自上而下的上滤
    - 自下而上的下滤
    - 效率对比
    - 复杂度计算
    - 实现
  - 完整代码
- 最小堆
- 比较器解析
- Top K 问题
- - 问题分析
  - 代码实现
  - 内部方法分析
  - 问题 2
- 堆排序
- - 概念
  - 代码示例
  - - 第一种 -- 降序
    - 第二种 -- 升序
  - 空间复杂度能否下降至 O(1)?
  - - 示例代码分析
    - 示例代码分析

需求分析

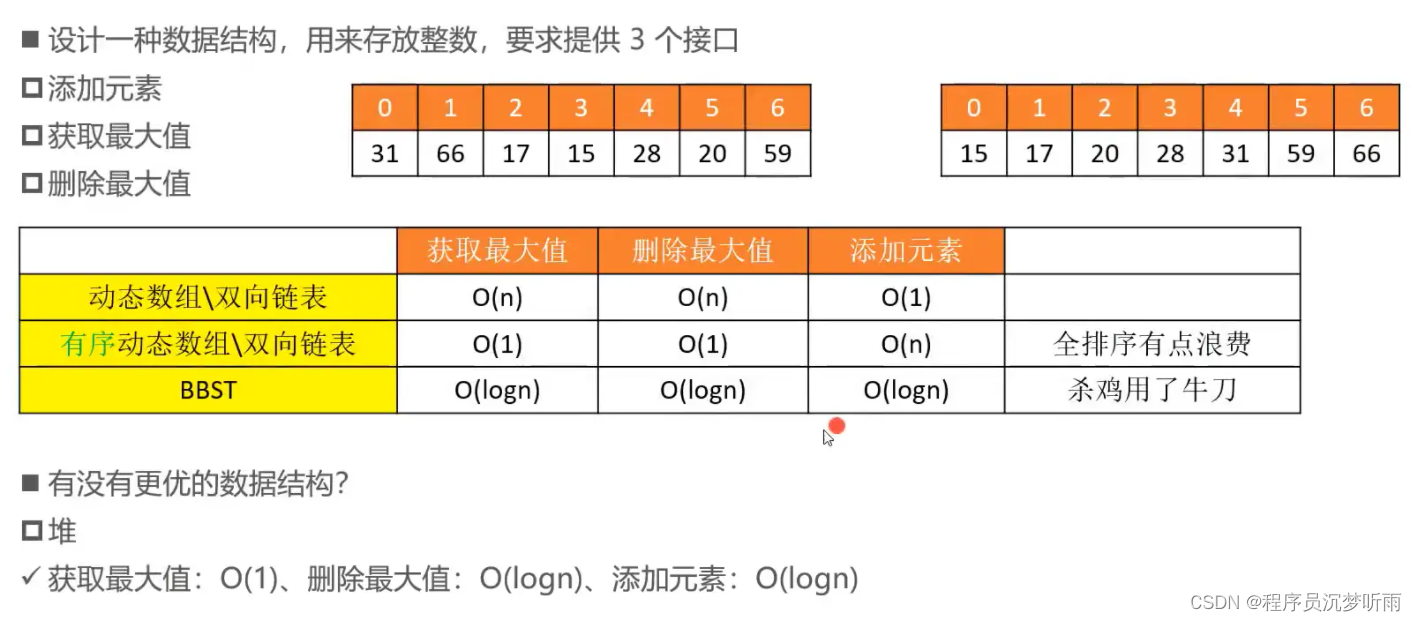
在这里插入图片描述

Top K 问题

什么是 Top K 问题？

从海量数据中找出前 K 个数据。

比如：从 100 万个整数中找出最大的 100 个整数
Top K 问题的解法之一：可以用数据结构 “堆” 来解决。

堆

堆是一种【完全二叉树】，可以分为【最大堆】和【最小堆】。只要是堆，里面的元素就会具备可比较性。

在最大堆中，父节点的值大于等于(>=)其子节点的值；
在最小堆中，父节点的值小于等于(<=)其子节点的值。

在这里插入图片描述

堆的基本接口设计

public interface Heap<E> {int size();	// 元素的数量boolean isEmpty();	// 是否为空void clear();	// 清空void add(E element);	 // 添加元素E get();	// 获得堆顶元素E remove(); // 删除堆顶元素E replace(E element); // 删除堆顶元素的同时插入一个新元素
}

二叉堆(Binary Heap)

着重注意索引的规律

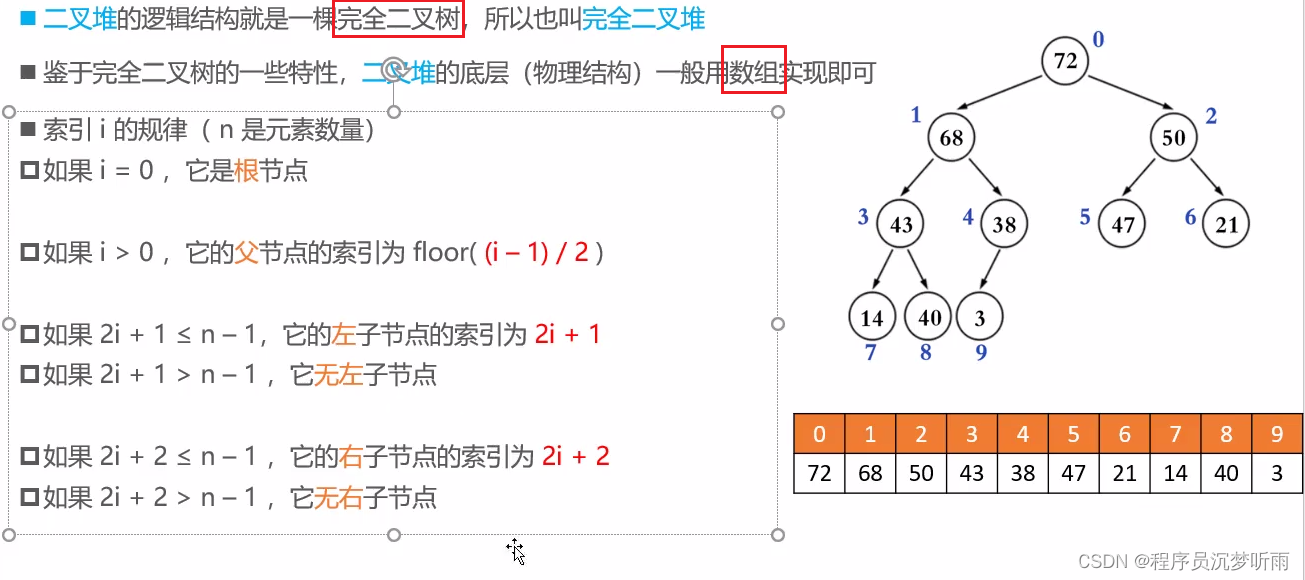
在这里插入图片描述

floor（向下取整）：只取前面的整数。

最大堆

添加

思路

一步步往上与父节点比较，并进行位置交换。

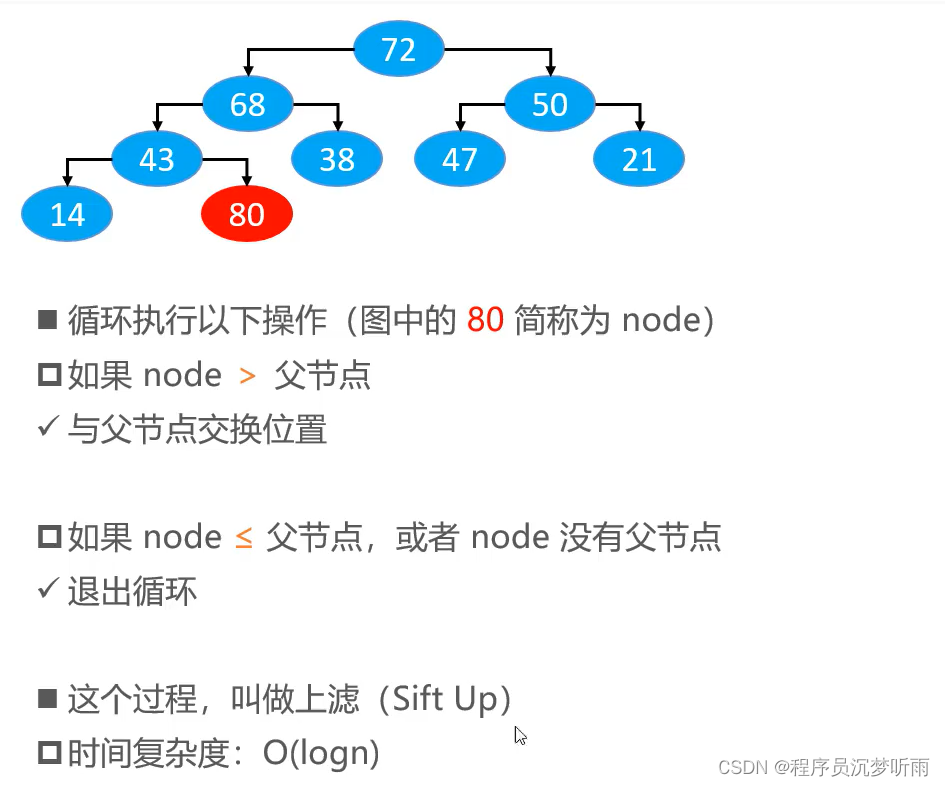
在这里插入图片描述

交换位置的优化

一般交换位置需要 3 行代码，可以进一步优化

将新添加节点备份，确定最终位置才摆放上去
循环比较，交换父节点位置 -> 循环比较，单纯父节点下移，最后确定位置了直接覆盖
省去了每次都交换位置并且覆盖的操作

实现

	@Overridepublic void add(E element) {elementNotNullCheck(element);ensureCapacity(size + 1);elements[size++] = element;siftUp(size - 1);}private void elementNotNullCheck(E element) {if (element == null) {throw new IllegalArgumentException("element must not be null");}}private void ensureCapacity(int capacity) {int oldCapacity = elements.length;if (oldCapacity >= capacity) {return;}// 新容量为旧容量的1.5倍int newCapacity = oldCapacity + (oldCapacity >> 1);E[] newElements = (E[]) new Object[newCapacity];for (int i = 0; i < size; i++) {newElements[i] = elements[i];}elements = newElements;}/*** 让index位置的元素上滤* @param index*/private void siftUp(int index) {
//		E e = elements[index];
//		while (index > 0) {
//			int pindex = (index - 1) >> 1;
//			E p = elements[pindex];
//			if (compare(e, p) <= 0) return;
//			
//			// 交换index、pindex位置的内容
//			E tmp = elements[index];
//			elements[index] = elements[pindex];
//			elements[pindex] = tmp;
//			
//			// 重新赋值index
//			index = pindex;
//		}E element = elements[index];while (index > 0) {int parentIndex = (index - 1) >> 1;E parent = elements[parentIndex];if (compare(element, parent) <= 0) {break;}// 将父元素存储在index位置elements[index] = parent;// 重新赋值indexindex = parentIndex;}elements[index] = element;}

删除

思路

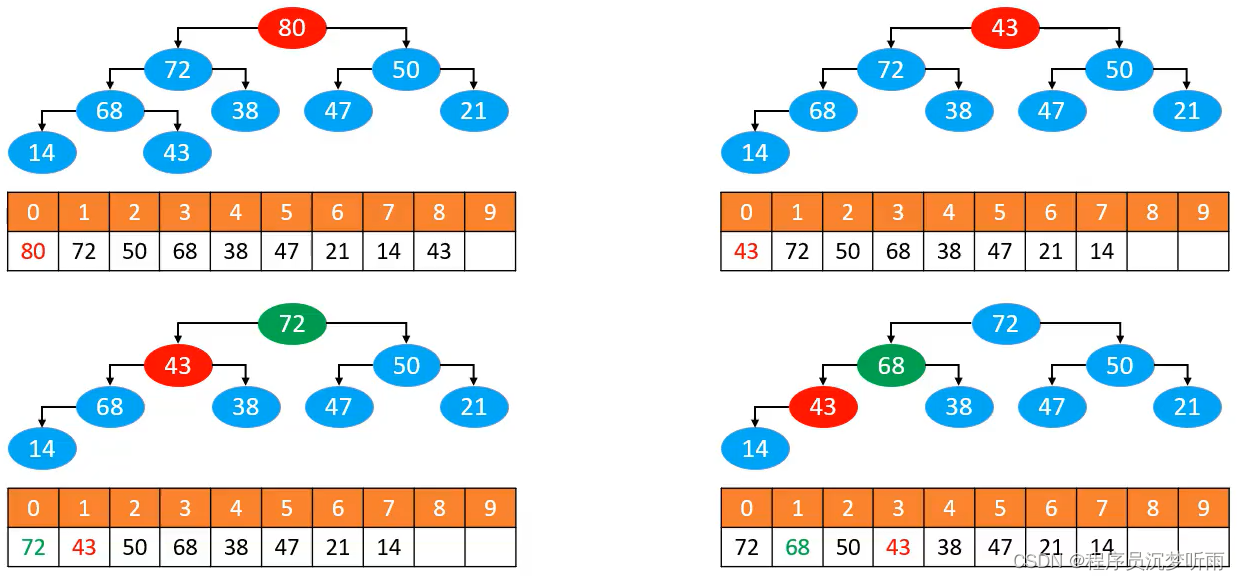
一般来说，如果我们要删除某个元素的话，我们通常会拿到最后一个元素先覆盖它的位置，然后再把最后一个元素删掉，相当于同学们直接将 43 的值覆盖掉 0 这个位置的值，要再把这个值清空。

为什么？

因为这个操作是 O(1) 级别的，删除最后一个元素。

具体流程如下图所示：
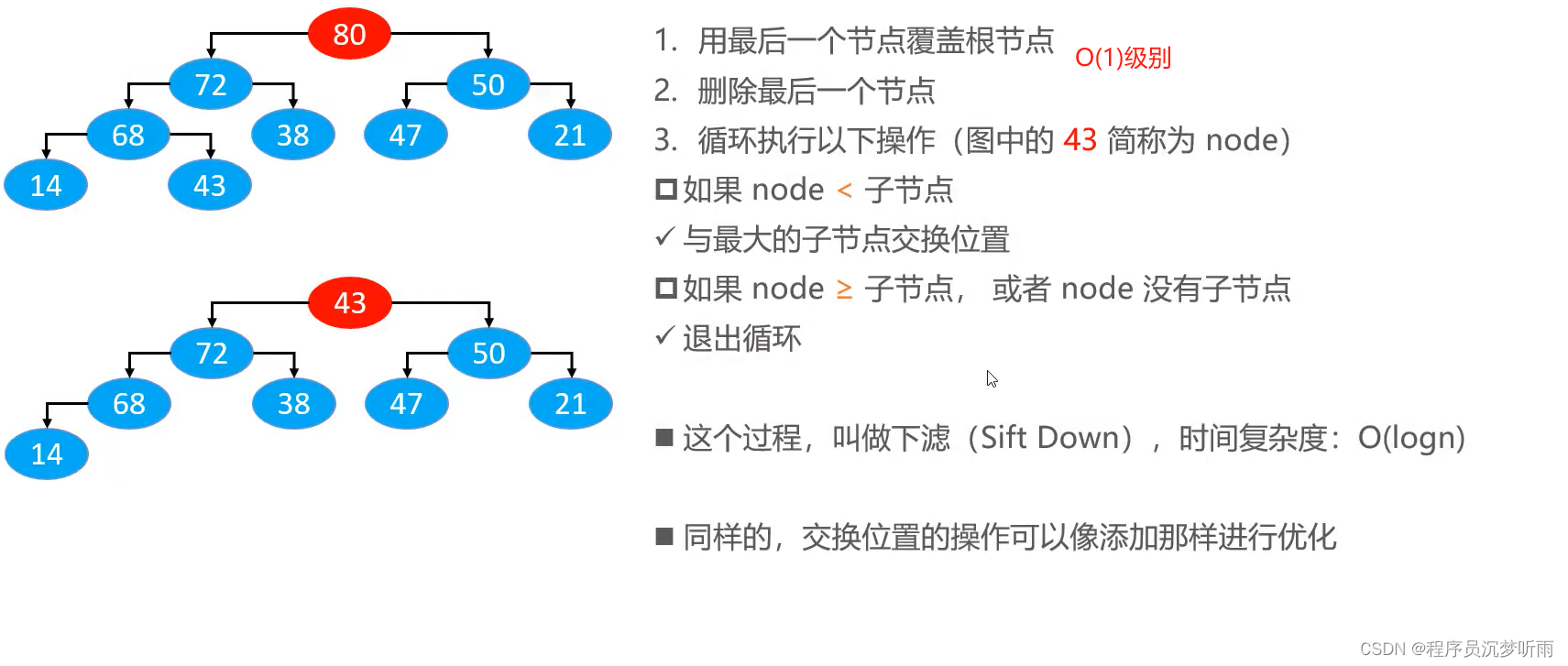
在这里插入图片描述

流程图解

在这里插入图片描述

实现

	@Overridepublic E remove() {emptyCheck();int lastIndex = --size;E root = elements[0];elements[0] = elements[lastIndex];elements[lastIndex] = null;siftDown(0);return root;}/*** 让index位置的元素下滤* @param index*/private void siftDown(int index) {E element = elements[index];int half = size >> 1;// 第一个叶子节点的索引 == 非叶子节点的数量// index < 第一个叶子节点的索引// 必须保证index位置是非叶子节点while (index < half) { // index的节点有2种情况// 1.只有左子节点// 2.同时有左右子节点// 默认为左子节点跟它进行比较int childIndex = (index << 1) + 1;E child = elements[childIndex];// 右子节点int rightIndex = childIndex + 1;// 选出左右子节点最大的那个if (rightIndex < size && compare(elements[rightIndex], child) > 0) {child = elements[childIndex = rightIndex];}if (compare(element, child) >= 0) {break;}// 将子节点存放到index位置elements[index] = child;// 重新设置indexindex = childIndex;}elements[index] = element;}

replace

接口：删除堆顶元素的同时插入一个新元素。

	@Overridepublic E replace(E element) {elementNotNullCheck(element);E root = null;if (size == 0) {elements[0] = element;size++;} else {root = elements[0];elements[0] = element;siftDown(0);}return root;}

批量建堆

批量建堆，有 2 种做法

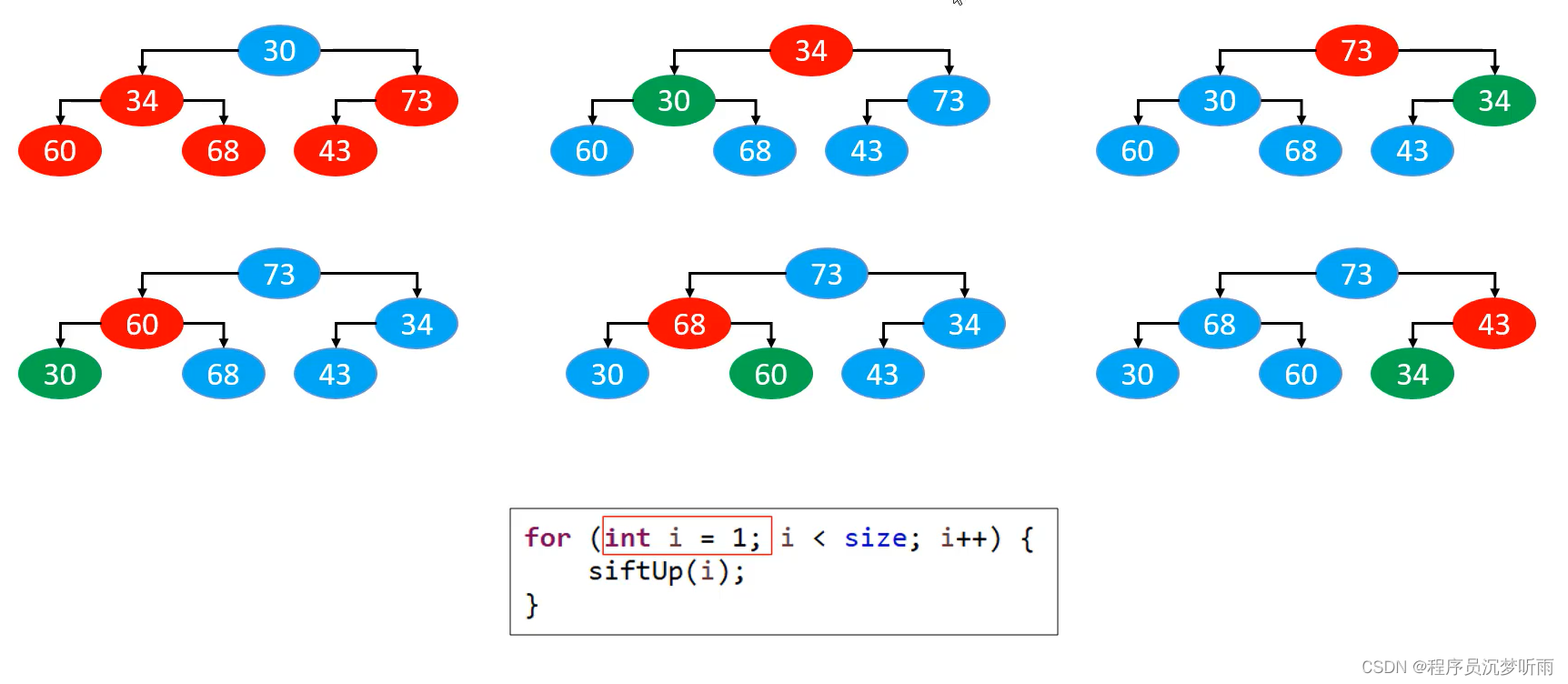
自上而下的上滤 – 本质是添加
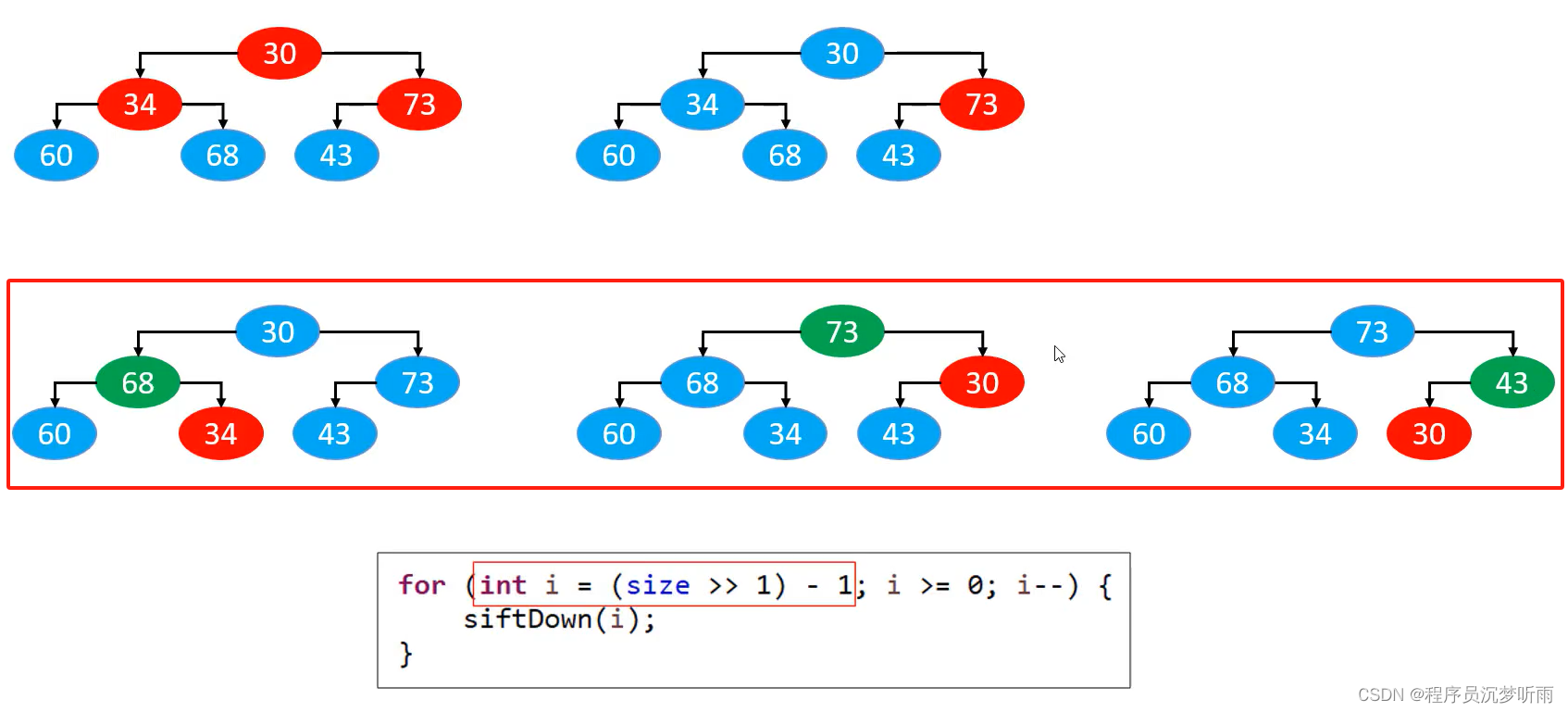
自下而上的下滤 – 本质是删除

注意：【自上而下的下滤】和【自下而上的上滤】不可以批量建堆，因为执行起来对整体来说没有什么贡献，依然还是乱的。

自上而下的上滤

在这里插入图片描述

自下而上的下滤

在这里插入图片描述

效率对比

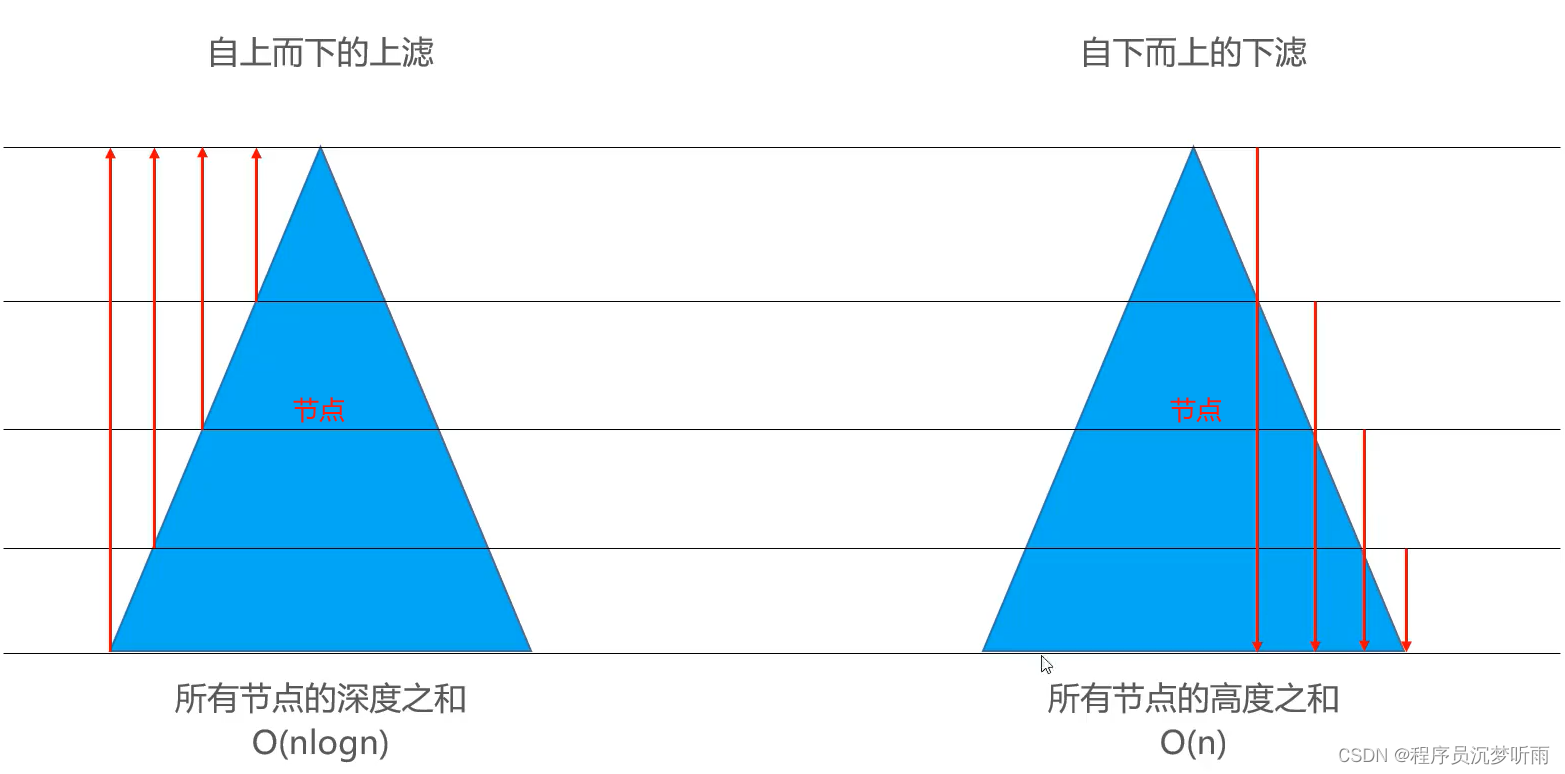
如下图所示，显然是【自下而上的下滤】效率更高。
可把图中蓝色部分看作是节点数量，箭头直线看作是工作量。
最下层的节点最多，这一部分在【自下而上的下滤】中的工作量较小。

在这里插入图片描述

复杂度计算

深度之和 vs 高度之和

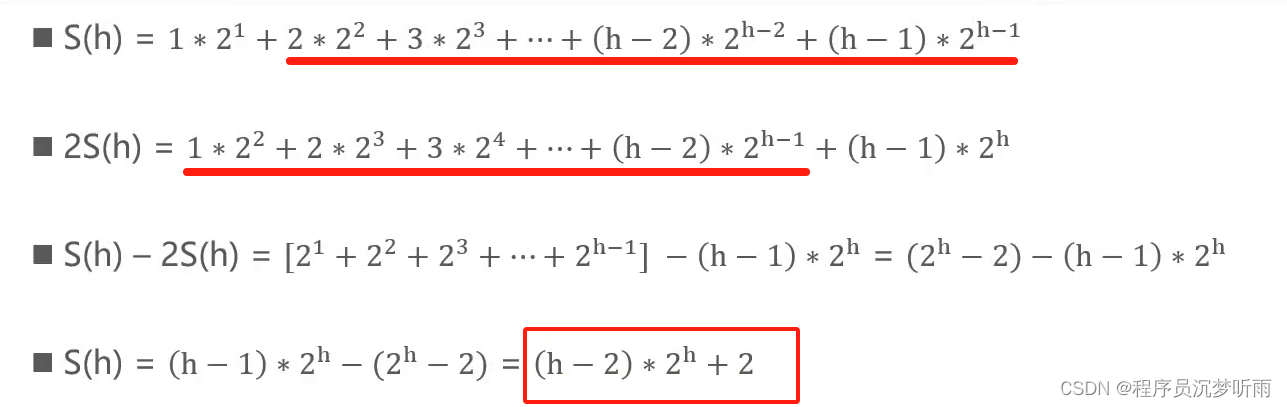
在这里插入图片描述

公式推导

在这里插入图片描述

实现

1、修改构造函数

	public BinaryHeap(E[] elements, Comparator<E> comparator)  {super(comparator);if (elements == null || elements.length == 0) {this.elements = (E[]) new Object[DEFAULT_CAPACITY];} else {size = elements.length;// this.elements = elements // 不能这么写，因为不安全int capacity = Math.max(elements.length, DEFAULT_CAPACITY);this.elements = (E[]) new Object[capacity];for (int i = 0; i < elements.length; i++) {this.elements[i] = elements[i];}// 批量建堆heapify();}}

解释：

this.elements = elements 会导致外部传进来的数组和堆内的数组挂钩，如果后续修改了外包数组的元素值，会影响批量建堆的输出。

2、批量建堆方法编写

	/*** 批量建堆*/private void heapify() {// 自上而下的上滤
//		for (int i = 1; i < size; i++) {
//			siftUp(i);
//		}// 自下而上的下滤for (int i = (size >> 1) - 1; i >= 0; i--) {siftDown(i);}}

完整代码

/*** 二叉堆（最大堆）*/
@SuppressWarnings("unchecked")
public class BinaryHeap<E> extends AbstractHeap<E> implements BinaryTreeInfo {private E[] elements;private static final int DEFAULT_CAPACITY = 10;public BinaryHeap(E[] elements, Comparator<E> comparator)  {super(comparator);if (elements == null || elements.length == 0) {this.elements = (E[]) new Object[DEFAULT_CAPACITY];} else {size = elements.length;int capacity = Math.max(elements.length, DEFAULT_CAPACITY);this.elements = (E[]) new Object[capacity];for (int i = 0; i < elements.length; i++) {this.elements[i] = elements[i];}heapify();}}public BinaryHeap(E[] elements)  {this(elements, null);}public BinaryHeap(Comparator<E> comparator) {this(null, comparator);}public BinaryHeap() {this(null, null);}@Overridepublic void clear() {for (int i = 0; i < size; i++) {elements[i] = null;}size = 0;}@Overridepublic void add(E element) {elementNotNullCheck(element);ensureCapacity(size + 1);elements[size++] = element;siftUp(size - 1);}@Overridepublic E get() {emptyCheck();return elements[0];}@Overridepublic E remove() {emptyCheck();int lastIndex = --size;E root = elements[0];elements[0] = elements[lastIndex];elements[lastIndex] = null;siftDown(0);return root;}@Overridepublic E replace(E element) {elementNotNullCheck(element);E root = null;if (size == 0) {elements[0] = element;size++;} else {root = elements[0];elements[0] = element;siftDown(0);}return root;}/*** 批量建堆*/private void heapify() {// 自上而下的上滤
//		for (int i = 1; i < size; i++) {
//			siftUp(i);
//		}// 自下而上的下滤for (int i = (size >> 1) - 1; i >= 0; i--) {siftDown(i);}}/*** 让index位置的元素下滤* @param index*/private void siftDown(int index) {E element = elements[index];int half = size >> 1;// 第一个叶子节点的索引 == 非叶子节点的数量// index < 第一个叶子节点的索引// 必须保证index位置是非叶子节点while (index < half) { // index的节点有2种情况// 1.只有左子节点// 2.同时有左右子节点// 默认为左子节点跟它进行比较int childIndex = (index << 1) + 1;E child = elements[childIndex];// 右子节点int rightIndex = childIndex + 1;// 选出左右子节点最大的那个if (rightIndex < size && compare(elements[rightIndex], child) > 0) {child = elements[childIndex = rightIndex];}if (compare(element, child) >= 0) {break;}// 将子节点存放到index位置elements[index] = child;// 重新设置indexindex = childIndex;}elements[index] = element;}/*** 让index位置的元素上滤* @param index*/private void siftUp(int index) {
//		E e = elements[index];
//		while (index > 0) {
//			int pindex = (index - 1) >> 1;
//			E p = elements[pindex];
//			if (compare(e, p) <= 0) return;
//			
//			// 交换index、pindex位置的内容
//			E tmp = elements[index];
//			elements[index] = elements[pindex];
//			elements[pindex] = tmp;
//			
//			// 重新赋值index
//			index = pindex;
//		}E element = elements[index];while (index > 0) {int parentIndex = (index - 1) >> 1;E parent = elements[parentIndex];if (compare(element, parent) <= 0) {break;}// 将父元素存储在index位置elements[index] = parent;// 重新赋值indexindex = parentIndex;}elements[index] = element;}private void ensureCapacity(int capacity) {int oldCapacity = elements.length;if (oldCapacity >= capacity) {return;}// 新容量为旧容量的1.5倍int newCapacity = oldCapacity + (oldCapacity >> 1);E[] newElements = (E[]) new Object[newCapacity];for (int i = 0; i < size; i++) {newElements[i] = elements[i];}elements = newElements;}private void emptyCheck() {if (size == 0) {throw new IndexOutOfBoundsException("Heap is empty");}}private void elementNotNullCheck(E element) {if (element == null) {throw new IllegalArgumentException("element must not be null");}}@Overridepublic Object root() {return 0;}@Overridepublic Object left(Object node) {int index = ((int)node << 1) + 1;return index >= size ? null : index;}@Overridepublic Object right(Object node) {int index = ((int)node << 1) + 2;return index >= size ? null : index;}@Overridepublic Object string(Object node) {return elements[(int)node];}
}

最小堆

同样使用最大堆的代码，只需要设置一个倒序比较器即可，将小的数认为比较大放在数组前面。

代码如下：

	static void test3() {Integer[] data = {88, 44, 53, 41, 16, 6, 70, 18, 85, 98, 81, 23, 36, 43, 37};BinaryHeap<Integer> heap = new BinaryHeap<>(data, new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {// 将原本【最大堆】中较小的值放前面，就实现了【最小堆】return o2 - o1;}});BinaryTrees.println(heap);}public static void main(String[] args) {test3();}

比较器解析

无论是 o1 - o2 还是 o2 - o1

只要返回正整数，就表示 o1 应该在 o2 的右边。
而返回负整数则表示 o1 应该在 o2 的左边。

示例说明：

1、向数组中加入 20，Integer[] data = {10, 20}

o1 - o2 = -10 – 10, 20

o2 - o1 = 10 – 20, 10

2、再向数组中加入 30，Integer[] data ={10, 20, 30}

o1 - o2：

10 - 30 = -20 – 10, 30, 20
20 - 30 = -10 – 【10, 20, 30】

o2 - o1：

30 - 10 = 20 – 30, 10
20 - 10 = 10 – 【30, 20, 10】

总结

无论是升序还是降序，只要返回正整数，就表示第一个元素应该在第二个元素的右边。

Top K 问题

问题分析

题目：从 n 个整数中，找出最大的前 k 个数 (k 远远小于 n)

如果使用【排序算法】进行全排序，需要 O(nlogn) 的时间复杂度。
如果使用【二叉堆】来解决，可以使用 O(nlogk) 的时间复杂度来解决
- 新建一个小顶堆
- 扫描 n 个整数

具体细节：

先将遍历到的前 k 个数放入堆中；
从第 k + 1 个数开始，如果大于堆顶元素，就使用 replace 操作(删除堆顶元素，将第 k + 1 个数添加到堆中)

代码实现

	static void test4() {// 新建一个小顶堆BinaryHeap<Integer> heap = new BinaryHeap<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});// 找出最大的前k个数int k = 3;Integer[] data = {51, 30, 39, 92, 74, 25, 16, 93, 91, 19, 54, 47, 73, 62, 76, 63, 35, 18, 90, 6, 65, 49, 3, 26, 61, 21, 48};for (int i = 0; i < data.length; i++) {if (heap.size() < k) { // 前k个数添加到小顶堆heap.add(data[i]); // logk} else if (data[i] > heap.get()) { // 如果是第k + 1个数，并且大于堆顶元素heap.replace(data[i]); // logk}}// O(nlogk)BinaryTrees.println(heap);}public static void main(String[] args) {test4();}

内部方法分析

1、heap.get() 获取堆顶元素

	@Overridepublic E get() {emptyCheck();return elements[0];}

2、heap.replace(data[i]);

删除堆顶元素的同时插入一个新元素，即将大于堆顶的数组元素加进去。

3、这是个最小堆

堆顶元素一直是最小的。

问题 2

如果是找出最小的前 k 个数呢？

用大顶堆
如果小于堆顶元素，就使用 replace 操作

堆排序

概念

堆排序（Heap Sort）是一种基于堆数据结构的排序算法，它利用了堆的特性来进行排序。

堆排序的基本思想如下：

构建最大堆（或最小堆）：将待排序的数组构建成一个最大堆（或最小堆）。
交换堆顶元素：将堆顶元素与当前未排序部分的最后一个元素交换位置。
调整堆：对交换后的堆进行调整，使其满足最大堆（或最小堆）的性质。
重复步骤 2 和 3，直到整个数组排序完成。

代码示例

以下是两个简单的堆排序示例代码：

第一种 – 降序

public class Main2 {public static void main(String[] args) {Integer[] arr = { 12, 11, 13, 5, 6, 7 };BinaryHeap<Integer> heap = new BinaryHeap<>(arr);heapSort(heap);}public static <E> void heapSort(BinaryHeap<E> heap) {int size = heap.size();for (int i = 0; i < size; i++) {// 删除后会再调整堆结构E max = heap.remove();System.out.print(max + " ");}}
}

输出结果为：

13 12 11 7 6 5

第二种 – 升序

public class HeapSort {public static void heapSort(Integer[] arr) {int n = arr.length;// 构建最大堆for (int i = n / 2 - 1; i >= 0; i--) {heapify(arr, n, i);}// 交换堆顶元素和未排序部分的最后一个元素，并调整堆for (int i = n - 1; i > 0; i--) {// 将堆顶元素与当前未排序部分的最后一个元素交换位置int temp = arr[0];arr[0] = arr[i];arr[i] = temp;// 调整堆heapify(arr, i, 0);}}// 调整堆，使其满足最大堆的性质public static void heapify(Integer[] arr, int n, int i) {int largest = i; // 初始化堆顶元素为最大值int left = 2 * i + 1; // 左子节点的索引int right = 2 * i + 2; // 右子节点的索引// 判断左子节点是否大于堆顶元素if (left < n && arr[left] > arr[largest]) {largest = left;}// 判断右子节点是否大于堆顶元素if (right < n && arr[right] > arr[largest]) {largest = right;}// 如果堆顶元素不是最大值，则交换堆顶元素和最大值，并继续调整堆if (largest != i) {int temp = arr[i];arr[i] = arr[largest];arr[largest] = temp;heapify(arr, n, largest);}}public static void main(String[] args) {Integer[] arr = { 12, 11, 13, 5, 6, 7 };System.out.println("原始数组：");for (int num : arr) {System.out.print(num + " ");}System.out.println("\n------------------------");BinaryHeap<Integer> heap = new BinaryHeap<>(arr);BinaryTrees.println(heap);System.out.println("==========================");heapSort(arr);System.out.println("\n排序后的数组：");for (int num : arr) {System.out.print(num + " ");}System.out.println("\n------------------------");BinaryHeap<Integer> heap2 = new BinaryHeap<>(arr);BinaryTrees.println(heap2);}
}

输出结果为：

原始数组：
12 11 13 5 6 7 
------------------------┌──13─┐│     │
┌─11─┐ ┌─12
│    │ │
5    6 7
==========================排序后的数组：
5 6 7 11 12 13 
------------------------┌──13─┐│     │┌─12─┐ ┌─7│    │ │
11    6 5

注意：

以下这个方法是会对【原数组】的值改变的，heapSort 方法会直接修改原始数组。这意味着在排序之后，原始数组的顺序会被改变。

如果你希望保持原始数组的不变，并在排序后得到一个新的已排序副本，可以使用以下方法：


// 在进行堆排序之前，创建一个原始数组的副本。
Integer[] arr = { 12, 11, 13, 5, 6, 7 };
Integer[] arrCopy = Arrays.copyOf(arr, arr.length);

空间复杂度能否下降至 O(1)?

在当前的实现中，二叉堆的空间复杂度是 O(n)，其中 n 是元素的数量。这是因为我们使用一个数组来存储堆的元素。

要将空间复杂度降低到 O(1)，我们需要修改数据结构的实现方式。
目前的实现方式(BinaryHeap<E>)是使用一个动态数组来存储元素，但这会占用 O(n) 的额外空间。

如果要将空间复杂度降低到 O(1)，我们可以考虑使用原始的输入数组来表示堆，而不是创建一个额外的数组。这意味着我们需要在原始数组上进行堆操作，而不是将元素复制到新的数组中。（比如上面写的第二种代码示例）

但是，这样做会对原始数组进行修改，并且在堆操作期间可能会打乱原始数组的顺序。因此，在实际应用中，这种修改可能会有限制，并且需要权衡空间和时间的复杂度。

总结起来，要将空间复杂度降低到 O(1)，需要在原始数组上进行操作，但这可能会对原始数组造成修改，并可能会有限制和权衡。具体的实现方式取决于具体的应用场景和需求。

示例代码分析

第一种示例方法复杂度解析

空间复杂度：

如果输入的元素个数为 n，且 n 大于 10，那么空间复杂度为 O(n)；否则，空间复杂度为 O(1)。

所以最坏空间复杂度为 O(n)。

时间复杂度：

构建二叉堆的过程具有 O(n) 的时间复杂度，其中 n 是输入数组的长度。
接下来，进行 n 次删除操作，每次删除操作的时间复杂度为 O(logn)。由于删除操作会调整堆的结构，保持最大堆的性质，因此每次删除操作的时间复杂度为O(logn)。
因此，总体上，堆排序的时间复杂度为 O(nlogn)。

第二种示例方法复杂度解析

空间复杂度：

在 heapSort 方法中，除了输入数组之外，没有使用额外的空间。因此，空间复杂度为 O(1)，即常数级别的空间复杂度。

时间复杂度：

构建最大堆的过程具有 O(n) 的时间复杂度，其中 n 是输入数组的长度。
接下来，进行 n-1 次堆调整和交换操作，每次操作的时间复杂度为 O(logn)。
因此，总体上，堆排序的时间复杂度为 O(nlogn)。
*。
目前的实现方式(BinaryHeap<E>)是使用一个动态数组来存储元素，但这会占用 O(n) 的额外空间。

示例代码分析

第一种示例方法复杂度解析

空间复杂度：

如果输入的元素个数为 n，且 n 大于 10，那么空间复杂度为 O(n)；否则，空间复杂度为 O(1)。

所以最坏空间复杂度为 O(n)。

时间复杂度：

构建二叉堆的过程具有 O(n) 的时间复杂度，其中 n 是输入数组的长度。
接下来，进行 n 次删除操作，每次删除操作的时间复杂度为 O(logn)。由于删除操作会调整堆的结构，保持最大堆的性质，因此每次删除操作的时间复杂度为O(logn)。
因此，总体上，堆排序的时间复杂度为 O(nlogn)。

第二种示例方法复杂度解析

空间复杂度：