Course1-Week2-多输入变量的回归问题

• 笔记主要参考B站视频“(强推|双字)2022吴恩达机器学习Deeplearning.ai课程”。
• 本篇笔记对应课程 Course1-Week2（下图中深紫色）。

---

1. 向量化和多元线性回归

  在上一周“单变量线性回归”的基础上，本周将继续拓展到“多元线性回归”（第1节）、“多项式回归”（第3节），并介绍加速梯度下降法收敛的技巧（第2节）。

1.1 多维特征

首先将单个特征扩展到多个特征，下面是机器学习术语：

• $m$：训练样本的总数。
• $n$：输入特征的总数。
• $\vec{X}$：全部的输入特征值，是一个二维向量，每一行表示一个样本，每一列表示所有样本的单个特征。
• ${\vec{x}}_j$：表示第$j$个特征概念(一维向量)，$j$的取值范围为$j=1,...,n$。
• ${\vec{x}}^{(i)}$：第$i$个训练样本的输入特征(一维向量)，$i$的取值范围为$i=1,...,m$。
• $x_j^{(i)}$：第$i$个训练样本的第$j$个特征，是单个值。如下图中，$x_4^{(3)}=30$。
• $y^{(i)}$：第$i$个训练样本的目标值，是单个值。
• $\vec{Y}$：全部的训练样本的特征值，是一维向量。

注：若无特殊说明，所有的一维向量都默认为列向量。

概念区分：

• 单变量线性回归(univariate linear regression)：只有单个特征的线性回归模型。
• 多元线性回归(multiple linear regression)：具有多维特征的线性回归模型。
• multivariate regression：不是上述“多元回归”！另有别的意思，后面介绍。

  如上图所示，将“房价预测”中的输入特征数量增加为4个：输入特征：房屋面积、卧室数量、房屋层数、房屋年龄。于是显然其线性回归模型也将从 $f_{w,b}(x)=wx+b$ 扩展为下面的向量形式：
$$\begin{array}{rl}{f}_{\vec{w},b}(\vec{x})& =w_1{x}_1+w_2{x}_2+...+w_4{x}_4+b\\ & =\sum _{j=1}^n{w}_j{x}_j+b\\ & =\vec{w}\cdot \vec{x}+b\end{array}$$

• $\vec{w}=[w_1,w_2,...,w_n{]}^T$：表示参数(列)向量。$w_i$表示当前特征对房屋价格影响。
• $b$：常数项参数。可以理解为房屋的基价(base price)。
• $\vec{x}=[x_1,x_2,...,x_n{]}^T$：表示单个样本的特征(列)向量。
• $\vec{w}\cdot \vec{x}$：表示两个向量的点积。

1.2 向量化

  简单来说，所谓“向量化”就是将分散的数字绑在一起进行处理。虽然概念很简单，但是“向量化”对于机器学习来说非常重要，因为它可以使模型更简洁、代码更简洁，并且也可以加速代码运行速度。比如下图给出了三种书写求和公式的方法。可以发现，使用向量形式的模型表达式最简洁、代码最少(一行)：

1. 一个一个写：很麻烦，耗时耗力，也不会加快代码计算。
2. for循环：每次只能计算单个乘法并相加，n很大时非常耗时。
3. 向量相乘：形式简洁、运行更快。这是因为 numpy.dot()可以并行计算所有乘法，再进行相加。甚至某些内置算法还会使用GPU加速运算。

注：Optional Lab介绍了一些NumPy的语法。

并且梯度下降法的迭代计算中，使用向量更新参数也会非常简洁。所以机器学习中尽量使用向量化代码。

1.3 用于多元线性回归的梯度下降法

  有了“向量化”的铺垫，本节将前面的单变量线性回归问题扩展到多元线性回归。首先使用“向量”重写模型，然后也就可以写出梯度下降法的“向量”形式，进而迭代计算出模型参数：
$$\begin{array}{rl}\text{Model}& :f_{\vec{w},b}(\vec{x})=\vec{w}\cdot \vec{x}+b\\ \text{Cost function}& :\underset{\vec{w},b}{\min }J(\vec{w},b)=\frac{1}{2m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}{)}^2\\ \begin{array}{r}\text{Gradient descent}\\ \text{repeat until convergence}\end{array}& :\{\begin{array}{rl}{w}_j& =w_j-\alpha \frac{\partial }{\partial w_j}J(\vec{w},b)=w_j-\frac{\alpha }{m}\sum _{i=1}^m[(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})\cdot x_j^{(i)}],j=1,2,...,n.\\ b& =b-\alpha \frac{\partial }{\partial b}J(\vec{w},b)=b-\frac{\alpha }{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})\end{array}\end{array}$$

• 模型中 $\vec{x}$ 表示单个样本的所有特征，是一维向量。
• $f_{\vec{w},b}({\vec{x}}^{(i)})$是一个值，$y^{(i)}$是一个值。

  除了梯度下降法，还有一类求解模型参数的方法——正规方程法(Normal rquation method)。此方法利用线性代数的知识，直接令代价函数的梯度 $\frac{\partial }{\partial \vec{w}}J(\vec{w},b)=\vec{0}$，便可以一步求解出代价函数极小点所对应的参数值：$\vec{w}=({\vec{X}}^T\vec{X}{)}^{-1}{\vec{X}}^T\vec{Y}$，见“详解正规方程”。但是这种方法有两个缺点：

1. 适用面小：仅适用于线性拟合，无法应用于其他方法，比如下周要学的“逻辑回归算法(logistic regression algorithm)”或者神经网络(Course2)。
2. 计算规模不能太大：如何特征值数量很大，矩阵的逆等求解非常慢。

正规方程法通常会包含在机器学习函数库中，我们无需关心具体的计算过程。对于大多数机器学习算法来说，梯度下降法仍然是推荐的方法。

本节Quiz：

1. In the training set below, what is $x_4^{(3)}$? Please type in the number below (this is an integer such as 123, no decimal points).
   Answer: 30
   

2. Which of the following are potential benefits of vectorization? Please choose the best option.
   √ It can make your code shorter.
   √ It allows your code to run more easily on parallel compute hardware.
   √ It makes your code run faster.
   √ All of the above.

3. To make gradient descent converge about twice as fast, a technique that almost always works is to double the learning rate $\alpha$.
   × True
   √ False

4. With polynomial regression, the predicted values $f_{w,b}(x)$ does not necessarily have to be a straight line (or linear) function of the input feature $x$.
   × False
   √ True

2. 使梯度下降法更快收敛的技巧

2.1 特征缩放

  特征缩放(feature scaling)可以使梯度下降法更快收敛。这主要是因为不同特征的取值范围有很大不同，但所有特征所对应的参数的学习率是一致的。这就导致取值范围较小的特征的参数，会“跟不上”取值范围较大的特征的参数变化。比如我们来看看“特征值大小”和其关联的“参数大小”的关系，首先将“房价预测”的问题简化成两个特征：

• $x_1$：房屋面积，范围是300~2000平方英尺。
• $x_2$：卧室数量，范围是0~5。

参数选择：显然取值范围更大的 $x_1$ 影响更大。

• $w_1=50,w_2=0.1,b=50$：计算出来的房屋价格是 $$100050.5k$，显然与实际的 $$500k$ 完全不符。
• $w_1=0.1,w_2=50,b=50$：计算出来的房屋价格是 $$500k$，正好等于房屋实际价格。

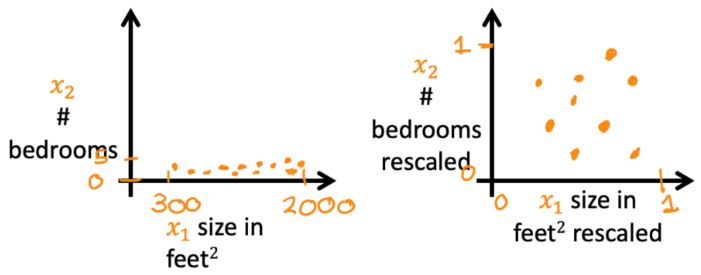
  于是，便考虑将 特征值归一化，使所有特征值的取值范围大致相同，这样就不会影响参数的迭代计算了。如下图便给出了进行 特征缩放 前后的对比：

左两图是训练样本散点图；右两图是代价函数等高图。上两图对应特征缩放前；下两图对应特征缩放后。

• 特征缩放前：散点图呈现条形，等高图呈极窄的椭圆形。这是因为对于范围较大的特征值($x_1$)所对应的参数$w_1$，一点微小的改变就会导致代价函数剧烈变化，进而使得等高图呈椭圆状。在使用梯度下降法的时候，由于学习率一样，每走一小步，就会导致代价函数在$w_2$方向变化不多、但在$w_1$方向急剧变化，于是就会“反复横跳”，增加迭代次数和计算量，甚至不能收敛。
• 特征缩放后：散点图分布较为均匀，并且等高图呈圆形。梯度下降法可以径直朝最小值迭代，减少迭代次数、更快的得到结果。

  好，现在我们知道进行 特征缩放 很有必要，那具体如何进行“特征缩放”，来使得所有特征都有相近的范围大小呢？主要有下面三种方法，并给出了第三种方法“Z-score归一化”的特征缩放效果：

1. 除以最大值：所有特征除以各自的范围最大值，使得特征值范围都在0~1之间。于是 $0.15\le \frac{x_1}{2000}\le 1$、$0\le \frac{x_2}{5}\le 1$。
2. 均值归一化(Mean normalization)：使得特征值范围大致为-1~1。假设$x_1$的平均值为${\mu }_1=600$、$x_2$的平均值为${\mu }_2=2.3$，于是 $-0.18\le \frac{x_1-{\mu }_1}{2000-300}\le 0.82$、$-0.46\le \frac{x_2-{\mu }_2}{5-0}\le 0.54$。
3. Z-score归一化(Z-score normalization)【推荐】：使得特征值服从标准正态分布。假设$x_1$的平均值和标准差分别为${\mu }_1=600,{\sigma }_1=450$、$x_2$的平均值和标准差分别为${\mu }_2=2.3,{\sigma }_2=1.4$，于是 $-0.67\le \frac{x_1-{\mu }_1}{{\sigma }_1}\le 3.1$、$-1.6\le \frac{x_2-{\mu }_2}{{\sigma }_2}\le 1.9$。

注：Z-score归一化的合理性在于自然界中大部分数据都是服从正态分布的。
均值：${\mu }_j=\frac{1}{m}{\sum }_{i=0}^{m-1}{x}_j^{(i)},j=0,1,...,n.$
方差：${\sigma }_j^2=\frac{1}{m}{\sum }_{i=0}^{m-1}(x_j^{(i)}-{\mu }_j{)}^2,j=0,1,...,n.$
标准差：${\sigma }_j=\sqrt{{\sigma }_j^2},j=0,1,...,n.$

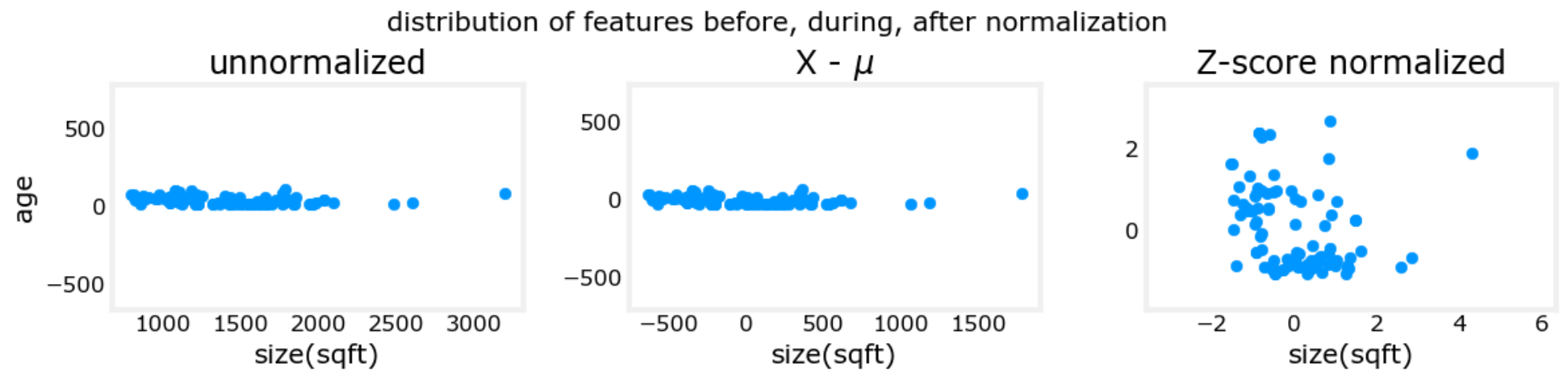
上面三个图的横纵坐标分别为两个特征：房屋面积、房屋年龄。可以看到特征缩放后，样本散点图分布的更加均匀。
下面两个图的横纵坐标同样是两个特征：房屋面积、卧室数量。可以看到特征缩放后，等高线图趋近圆形。
图片来自：C1_W2_Lab03_Feature_Scaling_and_Learning_Rate_Soln：

最后要说明一点，特征缩放后，只要所有特征值的范围在一个数量级就都可以接受，但若数量级明显不对等就需要 重新缩放。

2.2 判断梯度下降是否收敛

  本节主要介绍 横坐标为迭代次数 的“学习曲线(learning carve)”。学习曲线可以帮助我们判断梯度下降法 是否正在收敛，或者判断梯度下降法 是否已经收敛。如下图给出了正常的学习曲线，

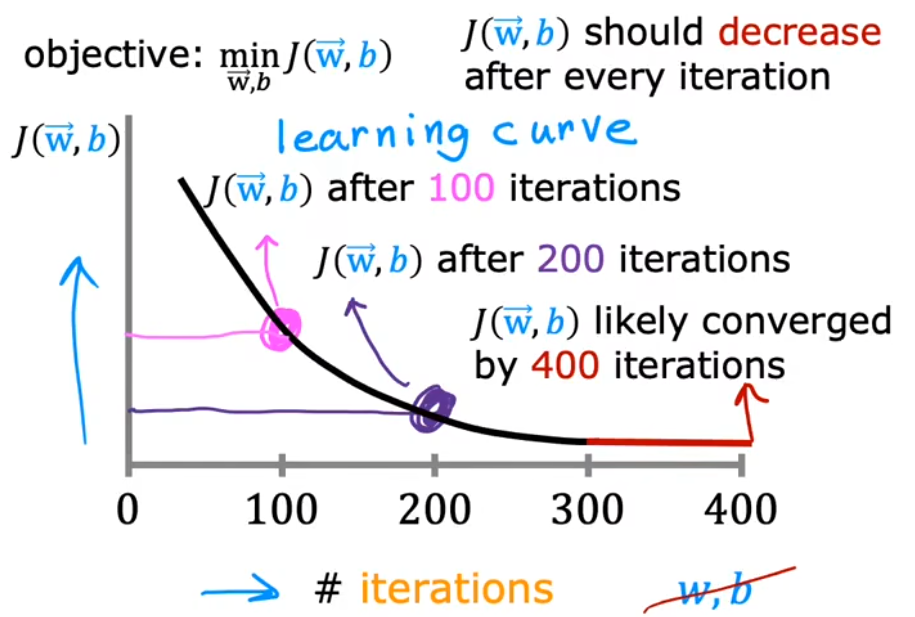
• 正常情况：每次迭代后，代价函数都应该下降。直到某次迭代后，代价函数几乎不再下降，就认为是收敛。
• 算法没有收敛：若某次迭代后，代价函数变大，则算法没有收敛，可能意味着学习率$\alpha$过大。
• 算法已经收敛：上图中的红色段，可以看到代价函数几乎不再下降。

自动收敛测试(automatic convergence test)：若两次迭代之间，代价函数的减少值$\le ϵ=10^{-3}$(自定义)，即可认为收敛。但是通常$ϵ$的选取很困难，所以还是建议使用上图所示的学习曲线进行判断。

注意不同的算法或问题，其收敛的迭代次数都不同，有些问题可能几十次就收敛，有些问题可能需要上万次才能收敛。由于很难提前知道梯度下降法是否会收敛，所以可以根据这个学习曲线来进行判断。

2.3 如何设置学习率

  之前提到，学习率太小，收敛太慢；学习率太大，可能不会收敛。那如何选择合适的学习率呢？正确的做法是，迭代较小的次数，快速地、粗略地选出合适的学习率。具体的选择策略是从一个较小的学习率(如0.01)开始，逐渐增大，直到出现不收敛的情况。如下图所示：

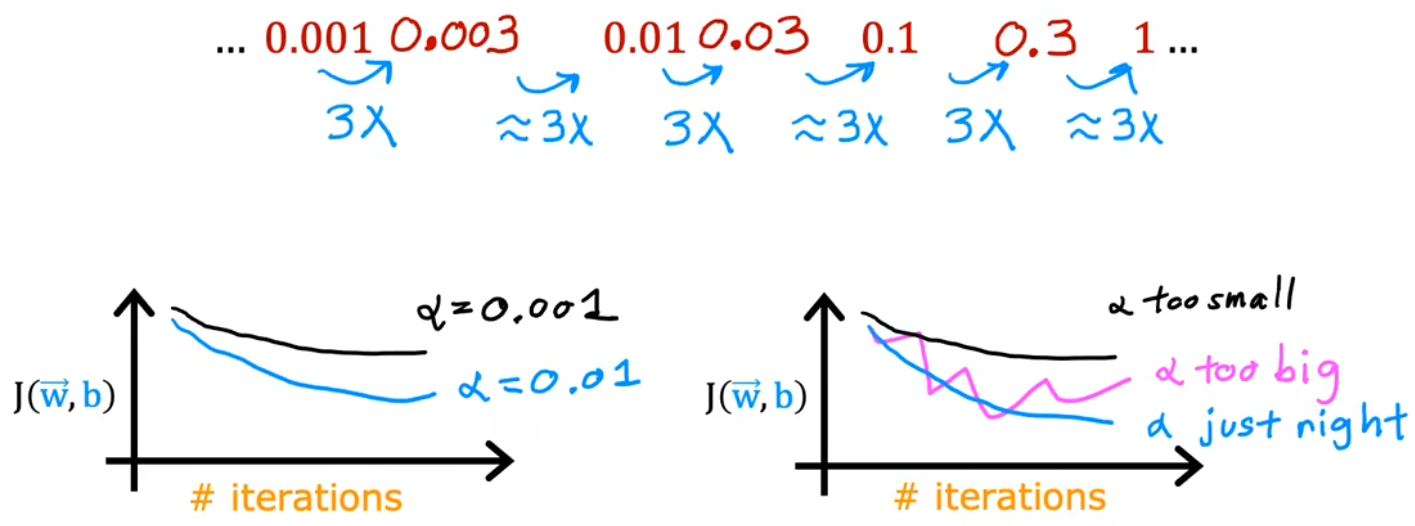
• 代价函数起伏不定：代码逻辑有bug(比如迭代方向写反)，或者学习率太大。
• 验证代码逻辑正常：当学习率很小时，代价函数会不断减小，即使很慢。

3. 特征工程

  “特征工程”这个标题听起来怪怪的，其实就是如何挑选、组合、使用“特征”的一套方法论。特征工程(Feature engineering)使用先验知识或直觉来转换或组合原始特征，从而设计出新的特征，进而简化算法或者使预测结果更准确。

关于Python仿真：scikit-learn是一个非常广泛使用的开源机器学习库，但是老师希望能理解线性回归的原理，而不是盲目地调用scikit-learn的函数。

3.1 选择合适的特征

  最简单的特征工程就是“选择合适的特征”。比如下图中，原始特征应该为房子所在地块的长度(frontage)和宽度(depth)，但占地面积(frontage × depth)应该是更符合直观的特征，于是就利用两个原始特征创造出了新的特征。

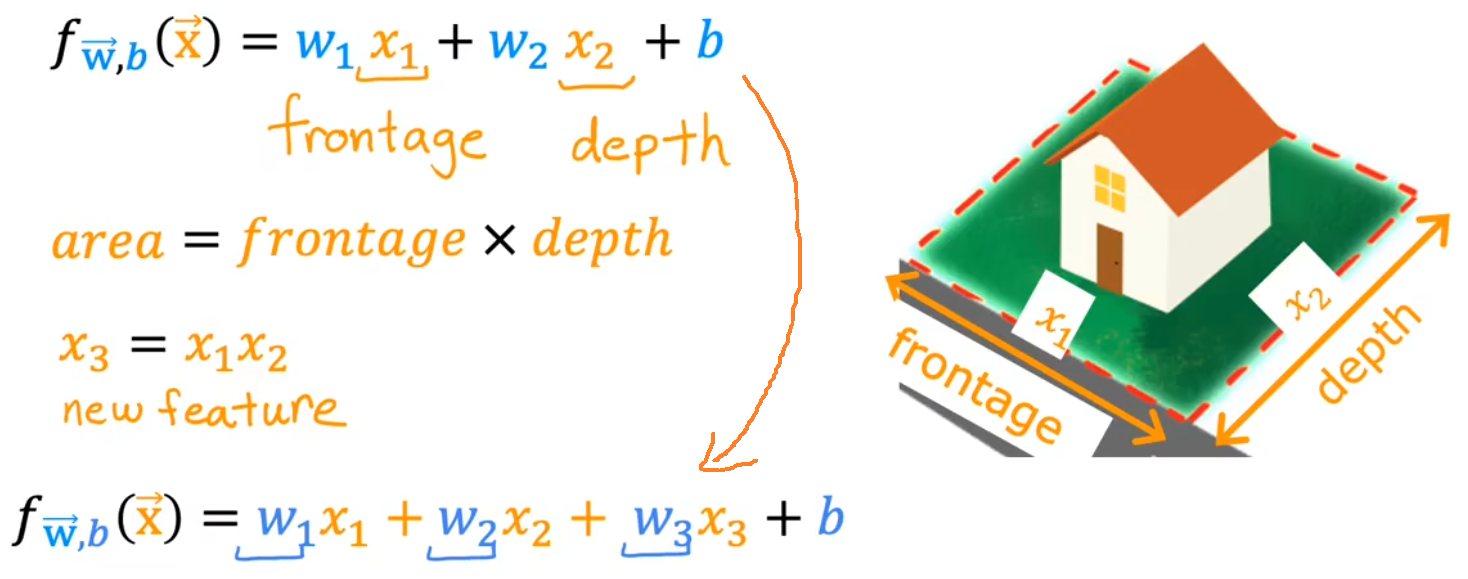
3.2 多项式回归

  另一种特征工程就是对某个特征进行幂次，进而实现使用非直线来拟合数据，也就是“多项式回归(Polynomial Regression)”。比如给出下图中红叉所示的训练样本，显然用直线拟合并不符合直观，于是：

• 二次函数拟合：虽然前半段看起来很好，但是终归会下降，这不符合“面积越大，房子越贵”的常识。
• 三次函数拟合：符合直觉，但后面房价随面积快速上升。
• 开根号拟合：符合直觉，房价随着面积缓慢上升。

注：幂次越高，特征缩放就显得越重要，否则参数的为微小变化将引起代价函数的剧烈波动，很可能会导致算法无法收敛。

在Course2中将介绍如何挑选不同的特征，现在只是明确用户可以挑选特征，并且使用“特征工程”和“多项式函数”可以拟合出曲线，来更加贴合样本。

1. Which of the following is a valid step used during feature scaling?
   × Add the mean (average) from each value and and then divide by the (max - min).
   √ Subtract the mean (average) from each value and then divide by the (max - min).
   

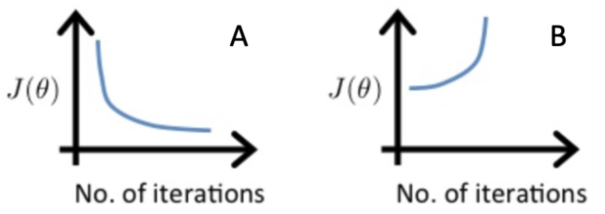
2. Suppose a friend ran gradient descent three separate times with three choices of the learning rate $\alpha$ and plotted the learning curves for each (cost $J$ for each iteration). For which case, A or B, was the learning rate a likely too large?
   √ case B only.
   × Both Cases A and B.
   × case A only.
   × Neither Case A nor B.
   

3. Of the circumstances below, for which one is feature scaling particularly helpful?
   × Feature scaling is helpful when all the features in the original data (before scaling is applied) range from 0 to 1.
   √ Feature scaling is helpful when one feature is much larger (or smaller) than another feature.
   注：本题想表达的意思是，原始特征值范围都在0~1附近时，就没必要进行特征缩放了。

4. You are helping a grocery store predict its revenue, and have data on its items sold per week, and price per item. What could be a useful engineered feature?
   √ For each product, calculate the number of items sold times(乘) price per item.
   × For each product, calculate the number of items sold divided(除) by the price per item.

注：C1_W2_Linear_Regression包含单变量线性回归、多线线性回归的练习题，值得一做。