---

---

什么是 $Trie$ 树

一种树结构，用来存储字符串，能够查询某字符串是否存在

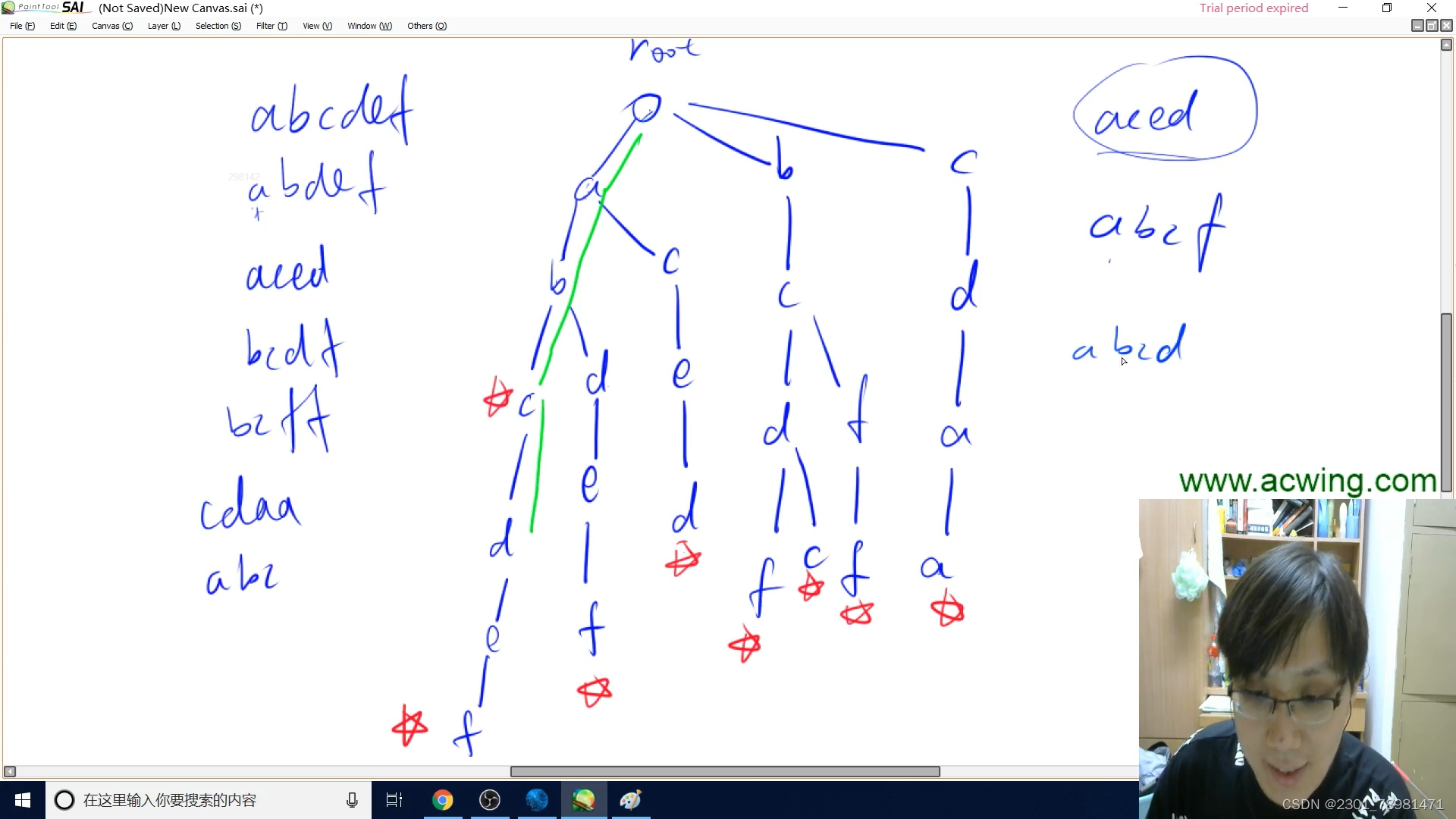
• 由一个统一的根节点 $root$ 发散开，存储字符
  • 如果下一个字符之前有用过，就顺着之前的路线往后走
  • 如果下一个字符与之前的某串不重合，就另开一个路线继续走下去
• 最后如果串存完了在末尾打个标记
  • 比如：之前存过字符串 ${}^{\prime }abcde{f}^{\prime }$，我们再存 ${}^{\prime }ab{c}^{\prime }$ 就会发现后者是前者的子串，如果不打标记就发现不了这个串

一般条件

一般题目中都会说明是全大写字母或者全小写字母，所以说数组开的范围不会太大，当然也有大范围。（我在写啥？？？《-_-》）

---

AcWing 835. Trie字符串统计

板子题：https://www.acwing.com/activity/content/problem/content/883/

CODE

#include <iostream>using namespace std;// 定义常量N为100010，这是我们预设的最大节点数量
const int N = 100010;// son数组用于存储每个节点的子节点，每个节点有26个子节点，对应26个英文字母
// cnt数组用于存储每个节点结束的单词数量
// idx用于节点编号，每当我们创建一个新节点时，idx会加1
// str用于存储输入的字符串
int son[N][26], cnt[N], idx;
char str[N];// 插入函数，用于将一个字符串插入到字典树中
void insert(char *str)
{// p是当前节点的编号，一开始我们在根节点，所以p=0int p = 0;// 遍历输入字符串的每个字符for (int i = 0; str[i]; i ++ ){// 计算当前字符对应的编号int u = str[i] - 'a';// 如果当前节点没有对应的子节点，我们就创建一个新节点if (!son[p][u]) son[p][u] = ++ idx;// 转移到子节点p = son[p][u];		// 不能标记为idx，因为可能前面部分串有过记录，用idx就不对了}// 遍历完字符串后，我们在一个节点结束，所以该节点的单词数量加1cnt[p] ++ ;				// 这个也是同理，不能用idx
}// 查询函数，用于查询一个字符串在字典树中出现的次数
int query(char *str)
{// p是当前节点的编号，一开始我们在根节点，所以p=0int p = 0;// 遍历输入字符串的每个字符for (int i = 0; str[i]; i ++ ){// 计算当前字符对应的编号int u = str[i] - 'a';// 如果当前节点没有对应的子节点，说明字符串不存在，返回0if (!son[p][u]) return 0;// 转移到子节点p = son[p][u];}// 返回当前节点的单词数量，即字符串在字典树中出现的次数return cnt[p];
}// 主函数
int main()
{// n是操作数量int n;scanf("%d", &n);// 处理每个操作while (n -- ){// op是操作类型，str是操作的字符串char op[2];scanf("%s%s", op, str);// 如果操作类型是"I"，则插入字符串if (*op == 'I') insert(str);// 否则，查询字符串并打印出现次数else printf("%d\n", query(str));}return 0;
}

解释一下 $insert()$ 函数

• 首先读入了待插入的字符串str
• 找到根节点 $root$ —> p = 0，也就是在son[0]位置是我们的根节点位置，由这个位置往后寻找
  • 先读入下一个字符，然后在后面 $26$ 个字符空间中看这个字符是否被标记过
    • 如果被标记过则说明之前的某一字符串的这部分跟插入的串重合，拿着标记号去跟着之前的串走，也就是代码：

    p = son[p][u];
    

    • 如果未标记则说明之前没有串跟它重合，则需要自己开一条线往后走，同时给这个字符赋予新的编号++idx，代表我走过这条路，索引号是idx，也就是代码：

    if (!son[p][u]) son[p][u] = ++ idx;
    

• 最后串读完了，打个标记，就是字符串最后的字符拿到的编号为索引的数量数组cnt[p]++
• 对于 $query()$ 函数也是一样的思路

$idx$ 的意义

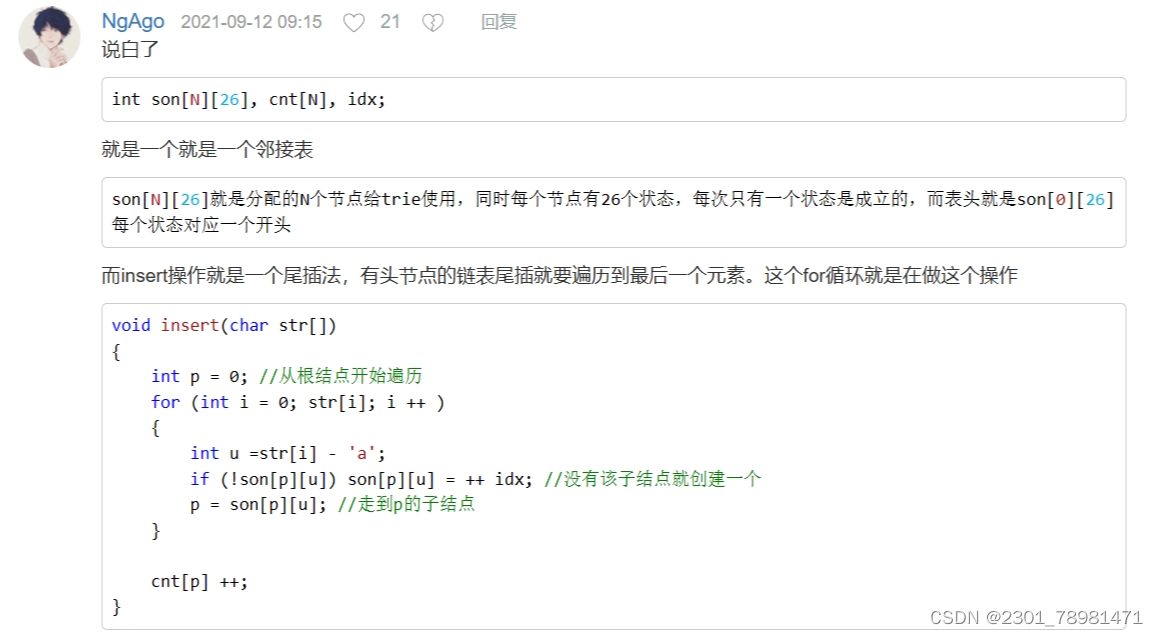
素材来源：https://www.acwing.com/solution/content/5673/ の评论区
还是评论区大神多啊，orz %%%

---

AcWing 143. 最大异或对

题目链接：https://www.acwing.com/activity/content/problem/content/884/

异或

• 异或俗称不进位加法，操作就是将两个二进制数的每一位对比，如果两位不一样(一个 $0$ 一个 $1$ )，那么就记为 $1$ ，否则记为 $0$
• 这种运算等价于将两个二进制数加起来，但是每位不进位

思路解析

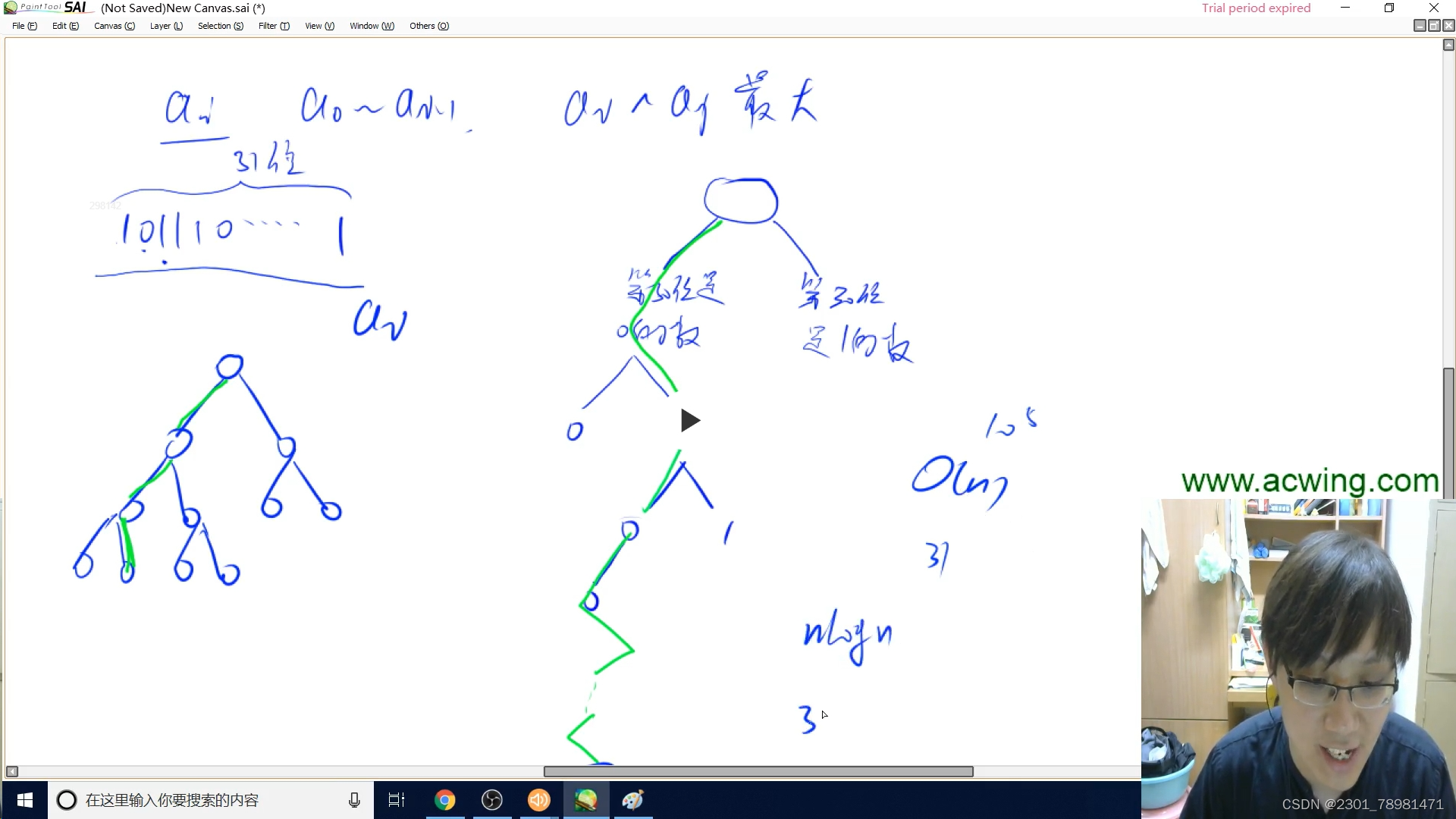
• 既然求异或最大，先固定一个数，遍历另一个数，那么最完美的情况就是每一位都不一样，此时异或值最大，虽然这个数存在是有可能的，但是存在一个这样的数不太可能。
• 那么虽然每一位完全不同的数可能不存在，那我们就利用贪心思想，每一位尽可能选择不一样的，最后得到的就是我们需要的数
• 由于是随机两个数进行组合，我们只需要固定一个数，然后枚举之前插入过 $Trie$ 树里面的数即可，最后再把这个数插入字典树

CODE

万事可暴力：

int main(){int n;cin >> n;for(int i = 0; i < n; ++i) scanf("%d", &a[i]);int res = 0;for(int i = 0; i < n; ++i){for(int j = 0; j < i; ++j){res = max(res, a[i] ^ a[j]);}}
}

充斥了暴力美学啊，可惜我猪脑不动的，暴力都没想到打。

$Trie$ 树

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10, M = 31 * N; // 定义数组的大小
int n; // 元素的数量
int son[M][2], idx; // Trie数据结构// 将一个数字插入到trie中的函数
void insert(int a){int p = 0;// 遍历每个位for(int i = 30; i >= 0; --i){int u = a >> i & 1;if(!son[p][u]) son[p][u] = ++idx;p = son[p][u];}
}// 查询函数
int query(int a){int p = 0, num = 0;for(int i = 30; i >= 0; --i){int u = a >> i & 1;if(son[p][!u]){num = (num << 1) + !u;p = son[p][!u];}else{num = (num << 1) + u;p = son[p][u];}}return num;
}int main()
{cin >> n;int a, res = 0;while (n -- ){scanf("%d", &a);insert(a);int t = query(a);res = max(res, a ^ t);}cout << res << endl;
}

代码解析

• 读入数a，先将其插入到字典树中，然后寻找树中插入过的数字与其“最大配偶”最接近的一个
  • $insert()$：将a按位插入字典树中，从高位到低位

    小 $Tip$：$int$ 类型只有 $31$ 位表示数据的值，最高位的 $0or1$ 代表了正负

  • $query()$：按位搜寻，如果存在位的值相反的数，那么就随着相反的值走，不存在就随相同的值走
• 将查询得到的配偶取异或，存最大值

---

给点思考

• 不管是 $Trie$ 还是字符哈希，他们好像都是查询作用的结构
  • $Trie$ 树：按每个字符进行查询
  • 字符哈希：按照区间进行查询
  • 所以说想要用字符串查询，用 $Trie$ 树；想要用区间 $[l,r]$ 来查询，得用哈希表
• 对于 $Trie$ 来说，理论上可以存储任何数据，因为所有数据终究是一堆 $0$ 和 $1$ ，那么用 $Trie$ 存的话就变成了一棵二叉树，所以说 $Trie$ 不仅可以存字符串，也可以存数字
• 如果我们再遇到从一堆数里面拿出两个进行操作时，我们可以像本题一样，先枚举第一个，第二个枚举到第一个数为止
  • 比如 $(1,2,3,4)$，我们i枚举到 $3$ ，i, j组合就是 $(1,3),(2,3),(3,3)$ ，那 $(4,3)$ 咋办？我们枚举 $4$ 的时候自然会枚举到 $(4,3)$。
  • 也就是公式$$C_n^2=\frac{n\times (n-1)}{2}$$