| 关卡名 | 理解树的前中后序遍历, 以及如何基于迭代方式实现 | 我会了✔️ |
| 内容 | 1.迭代实现二叉树树的前序遍历 | ✔️ |
| 2.迭代实现二叉树的中序遍历 | ✔️ | |
| 3.迭代实现二叉树的后序遍历 | ✔️ |
理论上,递归能做的迭代一定能做,但可能会比较复杂。上面几个递归的遍历方法,背都背下来了,所以有时候面试官要求不使用递归实现三种遍历,
递归就是每次执行方法调用都会先把当前的局部变量、参数值和返回地址等压入栈中,后面在递归返回的时候,从栈顶弹出上一层的各项参数继续执行,这就是递归为什么可以自动返回并执行上一层方法的原因。我们就用迭代法再次练习三道题:144.二叉树的前序遍历 94.二叉树的中序遍历 145.二叉树的后序遍历。
1 迭代法实现前序遍历
前序遍历是中左右,如果还有左子树就一直向下找。完了之后再返回从最底层逐步向上向右找。 不难写出如下代码: (注意代码中,空节点不入栈)
public List<Integer> preOrderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();if (root == null) {return res;}Deque<TreeNode> stack = new LinkedList<TreeNode>();TreeNode node = root;while (!stack.isEmpty() || node != null) {while (node != null) {res.add(node.val);stack.push(node);node = node.left;}node = stack.pop();node = node.right;}return res;
}此时会发现貌似使用迭代法写出前序遍历并不复杂,我们继续看中序遍历:
2 迭代法实现中序遍历
再看中序遍历,中序遍历是左中右,先访问的是二叉树左子树的节点,然后一层一层向下访问,直到到达树左面的最底部,再开始处理节点(也就是在把节点的数值放进res列表中)。在使用迭代法写中序遍历,就需要借用指针的遍历来帮助访问节点,栈则用来处理节点上的元素。 看代码:
public List<Integer> inorderTraversal(TreeNode root) {List<Integer> res = new ArrayList<Integer>();Deque<TreeNode> stack = new LinkedList<TreeNode>();while (root != null || !stack.isEmpty()) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();res.add(root.val);root = root.right;}return res;
}3 迭代法实现后序遍历
后序遍历的非递归实现有三种基本的思路:反转法、访问标记法、和Morris法,可惜三种理解起来都有些难度,如果头发不够,可以等一等再学习。
个人感觉访问标记法是最难理解的方法,而Morris法是一个老外发明的巧妙思想:不使用栈,而是用好树中的null指针,但是实现后序仍然非常麻烦,我们这里不再展开,感兴趣的同学可以查一下,
我们这里只介绍一种好理解又好实现的方法:反转法。
如下图,我们先观察后序遍历的结果是seq={9 5 7 4 3},如果我们将其整体反转的话就是new_seq={3 4 7 5 9}。
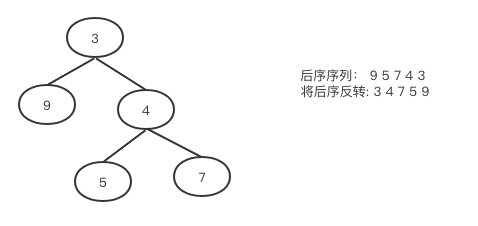
你有没有发现要得到new_seq的方法和前序遍历思路几乎一致,只不过是左右反了。前序是先中间,再左边然后右边,而这里是先中间,再后边然后左边。那我们完全可以改造一下前序遍历,得到序列new_seq之后再reverse一下就是想要的结果了,代码如下:
public List<Integer> postOrderTraversal(TreeNode root) {List<Integer> res = new ArrayList<>();if (root == null) return res;Stack<TreeNode> stack = new Stack<>();TreeNode node = root;while (!stack.isEmpty() || node != null) {while (node != null) {res.add(node.val);stack.push(node);node = node.right;}node = stack.pop();node = node.left;}Collections.reverse(res);return res;
}这个方法可以巧妙的避开直接后序时遇到的坑,那直接按照后序的规则写有难写问题呢?感兴趣的同学可以自己研究一下。