1. 题目链接：53. 最大子数组和

2. 题目描述：

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

示例 2：

输入：nums = [1]
输出：1

示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

• 1 <= nums.length <= 105
• -104 <= nums[i] <= 104

**进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

3. 解法（动态规划）：

3.1 算法思路：

1. 状态表示

以某一个位置为结尾，结合题目要求，定义一个状态表示：dp[i]表示：以i位置元素为结尾的所有子数组中和的最大和

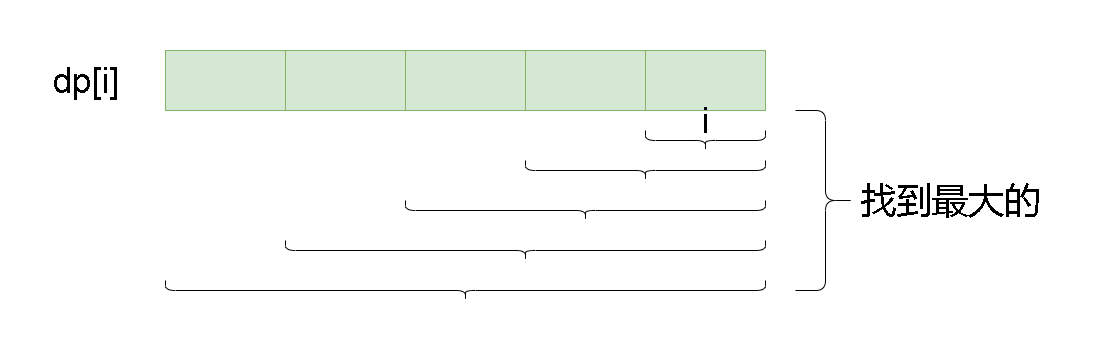
2. 状态转移方程：

dp[i]的所有可能可以分为以下两种：

1. 子数组的长度为1：此时 dp[i]=nums[i]
2. 子数组的长度大于 1：此时 dp[i]应该等于以 i-1做结尾所有子数组中和的最大值再加上 nums[i]，也就是 dp[i-1]+nums[i]
3. 由于我们要的是最大值，因此应该是两种情况下的最大值，因此可得转移方程：dp[i]=max(num[i],dp[i-1]+nums[i])
   

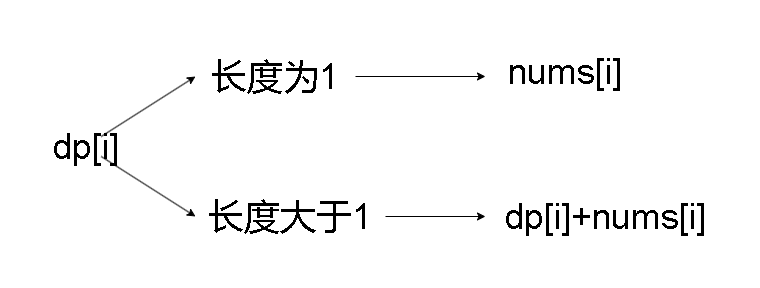
3. 初始化

可以在最前面加上一个辅助结点，帮助我们初始化。使用这种技巧要注意两点：

1. 辅助结点里面的值要保证后续填表是正确的
2. 下标的映射关系
3. 在最前面加上一个格子，并且让 dp[0]=0即可
   

4. 填表顺序

从左往右

5. 返回值

返回整个dp表中的最大值

3.2 C++算法代码：

class Solution {
public:int maxSubArray(vector<int>& nums) {// 获取数组长度int n = nums.size();// 初始化动态规划数组，长度为n+1，用于存储子问题的解vector<int> dp(n + 1);// 初始化最大子数组和为最小整数int ret = INT_MIN;// 遍历数组for (int i = 1; i <= n; i++) {// 更新动态规划数组，dp[i]表示以nums[i-1]结尾的最大子数组和dp[i] = max(nums[i - 1], dp[i - 1] + nums[i - 1]);// 更新最大子数组和ret = max(ret, dp[i]);}// 返回最大子数组和return ret;}
};