文章目录
- [数据结构]
- 1. String - 字符串
- 2. Linked List - 链表
- 2.1 链表的基本操作
- 2.1.1 反转链表
- 单向链表
- 双向链表
- 2.1.2 删除链表中的某个节点
- 2.1.3 链表指针的鲁棒性
- 2.1.4 快慢指针
- 3. Binary Tree - 二叉树
- 3.1 树的遍历
- 3.2 Binary Search Tree - 二叉查找树
- 4. Queue - 队列
- 4.1 Queue - 队列
- 4.2 Priority Queue - 优先队列
- 4.3 Deque - 双端队列
- 5. Heap - 堆
- 堆的基本操作
- 6. Stack - 栈
- 7. Set
- 8. Map - 哈希表
- 9. Graph - 图
[数据结构]
1. String - 字符串
开发常用,没啥可说的,注意的是字符串拼接时,可能会用到 StringBuffer 与 StringBuilder,前者保证线程安全,后者不是,但单线程下效率高一些,一般使用 StringBuilder。
2. Linked List - 链表
链表是线性表的一种。线性表是最基本、最简单、也是最常用的一种数据结构。
线性表有两种存储方式,一种是顺序存储结构(例如数组),另一种是链式存储结构。
链式存储结构就是两个相邻的元素在内存中可能不是相邻的,每一个元素都有一个指针域,指针域一般是存储着到下一个元素的指针。这种存储方式的优点是插入和删除的时间复杂度为 O(1),缺点是访问的时间复杂度最坏为 O(n)。
链表就是链式存储的线性表。根据指针域的不同,链表分为单向链表、双向链表、循环链表等等。
2.1 链表的基本操作
2.1.1 反转链表
单向链表
链表的基本形式是:1 -> 2 -> 3 -> null,反转需要变为 3 -> 2 -> 1 -> null。这里要注意:
- 访问某个节点 curt.next 时,要检验 curt 是否为 null。
- 要把反转后的最后一个节点(即反转前的第一个节点)指向 null。
class ListNode {int val;ListNode next;ListNode(int val) {this.val = val;}
}public ListNode reverse(ListNode head) {ListNode prev = null;while (head != null) {ListNode next = head.next;head.next = prev;prev = head;head = next;}return prev;
}
双向链表
和单向链表的区别在于:双向链表的反转核心在于next和prev域的交换,还需要注意的是当前节点和上一个节点的递推。
class DListNode {int val;DListNode prev, next;DListNode(int val) {this.val = val;this.prev = this.next = null;}
}public DListNode reverse(DListNode head) {DListNode curr = null;while (head != null) {curr = head;head = curr.next;curr.next = curr.prev;curr.prev = head;}return curr;
}
2.1.2 删除链表中的某个节点
删除链表中的某个节点一定需要知道这个点的前继节点,所以需要一直有指针指向前继节点。还有一种删除是伪删除,是指复制一个和要删除节点值一样的节点,然后删除,这样就不必知道其真正的前继节点了。
然后只需要把 prev -> next = prev -> next -> next 即可。
2.1.3 链表指针的鲁棒性
综合上面讨论的两种基本操作,链表操作时的鲁棒性问题主要包含两个情况:
- 当访问链表中某个节点 curt.next 时,一定要先判断 curt 是否为 null。
- 全部操作结束后,判断是否有环;若有环,则置其中一端为 null
2.1.4 快慢指针
所谓快慢指针中的快慢指的是指针向前移动的步长,每次移动的步长较大即为快,步长较小即为慢,常用的快慢指针一般是在单链表中让快指针每次向前移动2,慢指针则每次向前移动1。快慢两个指针都从链表头开始遍历,于是快指针到达链表末尾的时候慢指针刚好到达中间位置,于是可以得到中间元素的值。快慢指针在链表相关问题中主要有两个应用:
- 快速找出未知长度单链表的中间节点 设置两个指针
*fast、*slow都指向单链表的头节点,其中*fast的移动速度是*slow的2倍,当*fast指向末尾节点的时候,slow正好就在中间了。 - 判断单链表是否有环 利用快慢指针的原理,同样设置两个指针
*fast、*slow都指向单链表的头节点,其中*fast的移动速度是*slow的2倍。如果*fast = NULL,说明该单链表 以NULL结尾,不是循环链表;如果*fast = *slow,则快指针追上慢指针,说明该链表是循环链表。
3. Binary Tree - 二叉树
二叉树是每个节点最多有两个子树的树结构,子树有左右之分,二叉树常被用于实现二叉查找树和二叉堆。
public class TreeNode {public int val;public TreeNode left, right;public TreeNode(int val) {this.val = val;this.left = null;this.right = null;}
}
3.1 树的遍历
从二叉树的根节点出发,节点的遍历分为三个主要步骤:对当前节点进行操作(称为“访问”节点,或者根节点)、遍历左边子节点、遍历右边子节点。访问节点顺序的不同也就形成了不同的遍历方式。需要注意的是树的遍历通常使用递归的方法进行理解和实现,在访问元素时也需要使用递归的思想去理解。实际实现中对于前序和中序遍历可尝试使用递归实现。
按照访问根元素(当前元素)的前后顺序,遍历方式可划分为如下几种:
- 深度优先:先访问子节点,再访问父节点,最后访问第二个子节点。根据根节点相对于左右子节点的访问先后顺序又可细分为以下三种方式。
- 前序(pre-order):先根后左再右
- 中序(in-order):先左后根再右
- 后序(post-order):先左后右再根
- 广度优先:先访问根节点,沿着树的宽度遍历子节点,直到所有节点均被访问为止。
3.2 Binary Search Tree - 二叉查找树
一颗二叉查找树(BST)是一颗二叉树,其中每个节点都含有一个可进行比较的键及相应的值,且每个节点的键都大于等于左子树中的任意节点的键,而小于右子树中的任意节点的键。
使用中序遍历可得到有序数组,这是二叉查找树的又一个重要特征。
二叉查找树使用的每个节点含有两个链接,它是将链表插入的灵活性和有序数组查找的高效性结合起来的高效符号表实现。
4. Queue - 队列
4.1 Queue - 队列
Queue 是一个 FIFO(先进先出)的数据结构,并发中使用较多,可以安全地将对象从一个任务传给另一个任务。
Queue 在 Java 中是 Interface, 一种实现是 LinkedList 向上转型为 Queue, Queue 通常不能存储 null 元素,否则与 poll() 等方法的返回值混淆。
Queue<Integer> q = new LinkedList<Integer>();
int qLen = q.size(); // get queue length
| 0:0 | Throws exception | Returns special value |
|---|---|---|
| Insert | add(e) | offer(e) |
| Remove | remove() | poll() |
| Examine | element() | peek() |
优先考虑右侧方法,右侧元素不存在时返回 null. 判断非空时使用isEmpty()方法,继承自 Collection.
import java.util.LinkedList;
import java.util.Queue;public class QueueMethods {public static void main(String[] args) {Queue<Integer> q = new LinkedList<>();q.offer(1); // 增加元素q.offer(2); // 增加元素q.add(3); // 增加元素q.add(4); // 增加元素int size = q.size(); // 获取长度System.out.println("原始 q:" + q);/** remove 移除 Queue 的头部元素,并返回移除的元素* 移除时若队列为空,则报错:NoSuchElementException* 这也是它与 pull 方法的区别*/Integer remove = q.remove();System.out.println("remove 后 获取的元素 remove:" + remove);System.out.println("remove 后 q:" + q);Integer poll = q.poll();System.out.println("poll 后 获取的元素 poll:" + poll);System.out.println("poll 后 q:" + q);/** element 获取 Queue 的头部元素,并返回移除的元素* 移除时若队列为空,则报错:NoSuchElementException* 这也是它与 peek 方法的区别*/Integer element = q.element();System.out.println("element 后 获取的元素 element:" + element);System.out.println("element 后 q:" + q);Integer peek = q.peek();System.out.println("peek 后 获取的元素 peek:" + peek);System.out.println("peek 后 q:" + q);// 判断队列是否为空boolean empty = q.isEmpty();System.out.println("q 是否为空:" + empty);}
}
输出:
原始 q:[1, 2, 3, 4]
remove 后 获取的元素 remove:1
remove 后 q:[2, 3, 4]
poll 后 获取的元素 poll:2
poll 后 q:[3, 4]
element 后 获取的元素 element:3
element 后 q:[3, 4]
peek 后 获取的元素 peek:3
peek 后 q:[3, 4]
q 是否为空:false
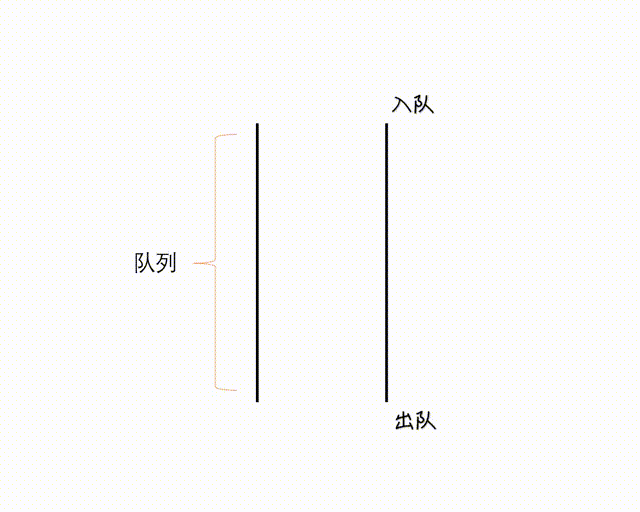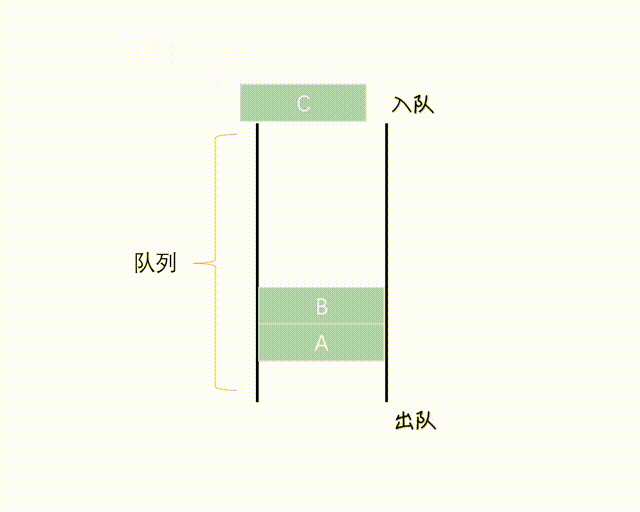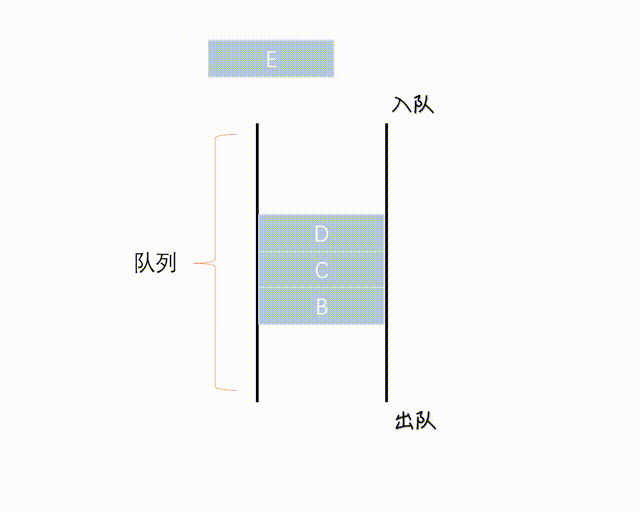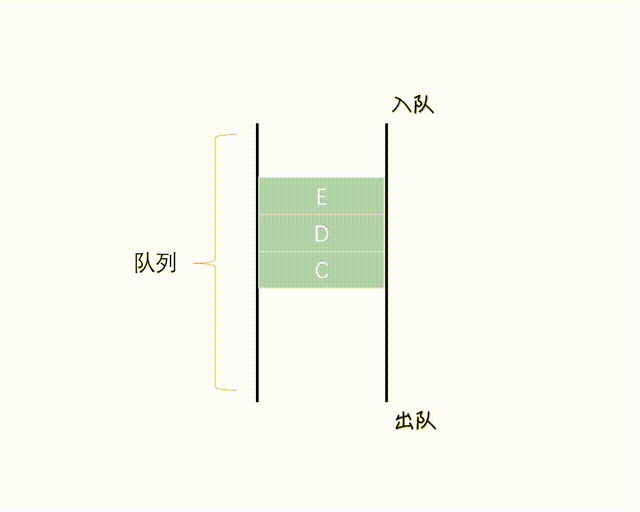
(图网,侵删)
4.2 Priority Queue - 优先队列
应用程序常常需要处理带有优先级的业务,优先级最高的业务首先得到服务。因此优先队列这种数据结构应运而生。优先队列中的每个元素都有各自的优先级,优先级最高的元素最先得到服务;优先级相同的元素按照其在优先队列中的顺序得到服务。
优先队列可以使用数组或链表实现,从时间和空间复杂度来说,往往用二叉堆来实现。
Java 中提供PriorityQueue类,该类是 Interface Queue 的另外一种实现,和LinkedList的区别主要在于排序行为而不是性能,基于 priority heap 实现,非synchronized,故多线程下应使用PriorityBlockingQueue. 默认为自然序(小根堆),需要其他排序方式可自行实现Comparator接口,选用合适的构造器初始化。使用迭代器遍历时不保证有序,有序访问时需要使用Arrays.sort(pq.toArray()).
4.3 Deque - 双端队列
双端队列(deque,全名double-ended queue)可以让你在任何一端添加或者移除元素,因此它是一种具有队列和栈性质的数据结构。
Java 在1.6之后提供了 Deque 接口,既可使用ArrayDeque(数组)来实现,也可以使用LinkedList(链表)来实现。前者是一个数组外加首尾索引,后者是双向链表。
Deque<Integer> deque = new ArrayDeque<Integer>();
| First Element (Head) | Last Element (Tail) | |||
|---|---|---|---|---|
| Throws exception | Special value | Throws exception | Special value | |
| Insert | addFirst(e) | offerFirst(e) | addLast(e) | offerLast(e) |
| Remove | removeFirst() | pollFirst() | removeLast() | pollLast() |
| Examine | getFirst() | peekFirst() | getLast() | peekLast() |
其中offerLast和 Queue 中的offer功能相同,都是从尾部插入。
5. Heap - 堆
一般情况下,堆通常指的是二叉堆,二叉堆是一个近似完全二叉树的数据结构,即披着二叉树羊皮的数组,故使用数组来实现较为便利。子结点的键值或索引总是小于(或者大于)它的父节点,且每个节点的左右子树又是一个二叉堆(大根堆或者小根堆)。根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常被用作实现优先队列。
堆的基本操作
以大根堆为例,堆的常用操作如下。
- 最大堆调整(Max_Heapify):将堆的末端子节点作调整,使得子节点永远小于父节点
- 创建最大堆(Build_Max_Heap):将堆所有数据重新排序
- 堆排序(HeapSort):移除位在第一个数据的根节点,并做最大堆调整的递归运算
其中步骤1是给步骤2和3用的。
—PS:这本书里有很多这种动图,简直就是神器
6. Stack - 栈
栈是一种 LIFO(Last In First Out) 的数据结构,常用方法有添加元素,取栈顶元素,弹出栈顶元素,判断栈是否为空。
import java.util.ArrayDeque;
import java.util.Deque;
import java.util.Stack;public class StackMethods {public static void main(String[] args) {/** JDK doc 中建议使用Deque代替Stack实现栈,* 因为Stack继承自Vector,需要synchronized,性能略低。*/Stack<Integer> stack = new Stack<>();Deque<Integer> s = new ArrayDeque<>();// E push(E item) - 向栈顶添加元素s.push(1);s.push(2);s.push(3);System.out.println("原始栈:" + s);System.out.println("原始栈,长度:" + s.size());// E peek() - 取栈顶元素,不移除Integer peek = s.peek();System.out.println("获取的栈顶元素:" + peek);System.out.println("peek 栈,长度:" + s.size());// E pop() - 移除栈顶元素并返回该元素Integer pop = s.pop();System.out.println("获取的栈顶元素:" + pop);System.out.println("pop 栈,长度:" + s.size());// 判断栈是否为空,若使用 Stack 类构造则为 empty()System.out.println("Deque 创建栈是否为空:" + s.isEmpty());System.out.println("Stack 创建栈是否为空:" + stack.empty());}
}
输出:
原始栈:[3, 2, 1]
原始栈,长度:3
获取的栈顶元素:3
peek 栈,长度:3
获取的栈顶元素:3
pop 栈,长度:2
Deque 创建栈是否为空:false
Stack 创建栈是否为空:true
7. Set
Set 是一种用于保存不重复元素的数据结构。常被用作测试归属性,故其查找的性能十分重要。
Set 与 Collection 具有安全一样的接口,通常有HashSet, TreeSet 或 LinkedHashSet三种实现。HashSet基于散列函数实现,无序,查询速度最快;TreeSet基于红-黑树实现,有序。
8. Map - 哈希表
Map 是一种关联数组的数据结构,也常被称为字典或键值对。
Java 的实现中 Map 是一种将对象与对象相关联的设计。常用的实现有HashMap和TreeMap, HashMap被用来快速访问,而TreeMap则保证『键』始终有序。Map 可以返回键的 Set, 值的 Collection, 键值对的 Set.
Map<String, Integer> map = new HashMap<String, Integer>();
map.put("bill", 98);
map.put("ryan", 99);
boolean exist = map.containsKey("ryan"); // check key exists in map
int point = map.get("bill"); // get value by key
int point = map.remove("bill") // remove by key, return value
Set<String> set = map.keySet();
// iterate Map
for (Map.Entry<String, Integer> entry : map.entrySet()) {String key = entry.getKey();int value = entry.getValue();// do some thing
}
9. Graph - 图
图的表示通常使用邻接矩阵和邻接表,前者易实现但是对于稀疏矩阵会浪费较多空间,后者使用链表的方式存储信息但是对于图搜索时间复杂度较高。
/* Java Definition */
int[][] g = new int[V][V];
(图网,侵删)