1 二分查找

1.1 重要概念

• 拟解决的问题：判断某个区间是否包含某个元素，无法确定区间中包含重复元素的具体位置；
• 使用条件：查找的区间必须符合单调性；
• 本质：采用分治思想，将某个单调区间一分为二，保证留下的一半区间包含解，舍弃的一半区间不包含解；
• 时间复杂度：O(log2n)�(���2�)
• 计算方式：二分查找每查找一次将原问题的规模n缩减到1/2，最糟糕的情况为n=1时，二分查找获得结果，此时二分查找的次数为$n/2^x=1，即，即x = log_2n$

1.2 应用场景

• 判断某个单调区间是否包含某个元素；
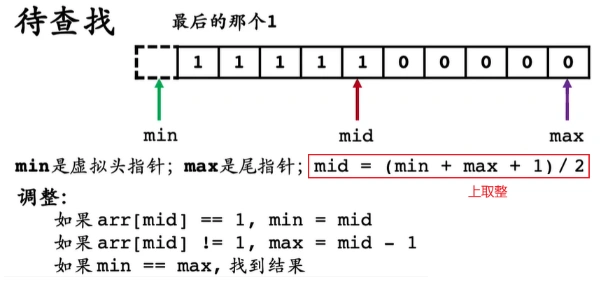
• 前面一堆1，后面一堆0，如1111100000，查询最后一个1出现的位置；（特殊情况1）
• 前面一堆0，后面一堆1，如0000011111，查询第一个1出现的位置；（特殊情况2）

1.3 代码演示

// 1 3 5 7 9 10
int binary_search(int *arr, int n ,int x) {int head = 0, tail = n - 1, mid;while (head <= tail) {mid = (head + tail) >> 1;if (arr[mid] == x) return mid;if (arr[mid] < x) head = mid + 1;else tail = mid - 1;}return -1;
}// 1111100000
int binary_search1(int *arr, int n) {int head = -1, tail = n - 1, mid;   // 当查找区间的元素全0时，为避免二义性，定义head=-1，而不是head=0while (head < tail) {mid = (head + tail + 1) >> 1;   // 上取整，否则会出现死循环if (arr[mid] == 1) head = mid;  // mid 有可能是最后一个1出现的位置else tail = mid -1;}// head = tail = -1 时，代表未找到，否则返回对应元素的位置return head;
}// 00000111111
int binary_search2(int *arr, int n) {int head = 0, tail = n, mid;        // 当查找区间的元素全0时，为避免二义性，定义tail=n，而不是tail=n-1while (head < tail) {mid = (head + tail) >> 1;if (arr[mid] == 1) tail = mid;  // mid 有可能是第一个1出现的位置else head = mid + 1;}// head = tail = n 时，代表未找到，否则返回对应元素的位置return head == n ? -1 : head;
}

2 三分查找

2.1 拟解决的问题

二分查找解决的是在单调序列中查找目标值的问题，而三分查找则是确定函数在凹/凸区间上的极值点；

2.2 算法描述

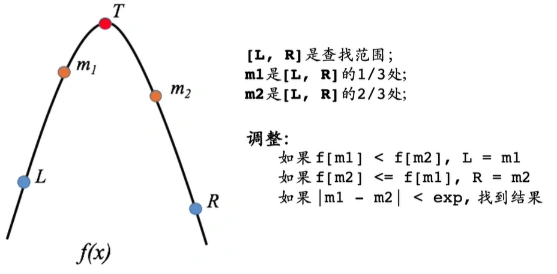
    在函数f(x)的某个区间[l, r]上取2个分界点，其中m1位于l的1/3处，m2位于l的2/3处，即：$m1 = l + (r - l) / 3$，$m2 = r - (r - l) / 3$，这两个点m1、m2把区间 [l, r] 分为3 个子区间。这里以凸函数（即有最大值）为例讨论：

• 若f(m1) < f(m2)，说明极值点位于[m1, r]区间内，可以不必再考虑[l, m1]区间；原因就是当f(m1) < f(m2)时，m1处于单调递增区间段，故f(l) < f(m1)；
• 若f(m1) > f(m2)，说明极值点位于[l, m2]区间内，可以不必再考虑[m2, r]区间；原因就是当f(m1) > f(m2)时，m2处于单调递减区间段，故f(m2) > f(r)；
• 这样，每一轮迭代都会把查找范围限制在原来的2/3，直到最终逼近极值点，即l和r之间的差值接近无穷小；
• 三分查找的时间复杂度：O(log3n)�(���3�)，二分查找的时间复杂度：O(log2n)�(���2�)，尽管二者的复杂度级别一样，但是二分查找的效率更高，因为二分查找是在1/2的区域寻找值，而三分查找是在2/3的区域寻找值；
• 参考博客：三分查找（ternary search）及其示例 - 简书、二分查找和三分查找哪个快？算法复杂度与常数无关？复杂度分析的常见误区 - 知乎

2.3 代码演示

double three_point_search(double (*func)(double), double l, double r) {double m1, m2;int flag = 0; // flag = 0：func 函数为凸函数；flag = 1：func 函数为凹函数// 凹凸函数判断if (func((l + r) / 2.0) > (func(l) + func(r)) / 2.0 ) flag = 0;else flag = 1;#define EPSL 1e-6if (!flag) {while (fabs(r - l) > EPSL) {m1 = l + (r - l) / 3.0, m2 = r - (r - l) / 3.0;if (func(m1) < func(m2)) l = m1;else r = m2;}} else {while (fabs(r - l) > EPSL) {printf("l = %f, r = %f\n", l, r);m1 = l + (r - l) / 3.0, m2 = r - (r - l) / 3.0;if (func(m1) < func(m2)) r = m2;else l = m1;}}#undef EPSLreturn l;
}

3 哈希表 HashTable

3.1 介绍

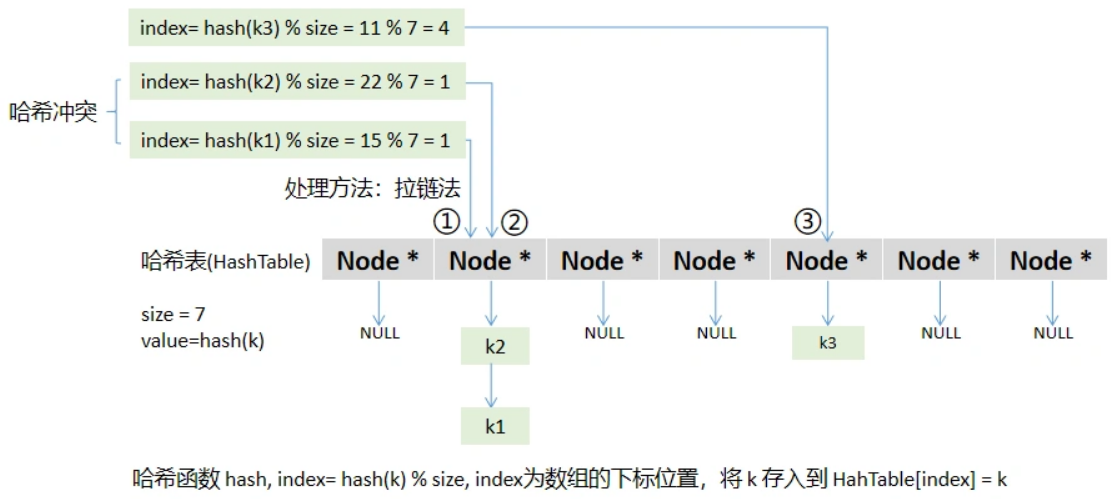
   基于数组的“随机访问”特性，其可以通过下标快速地找到对应位置的元素，然而这种通过`<int>`下标寻找`<任意类型>`元素的映射关系并不通用（映射关系：`<int>`→`<任意类型>`）。所以，为了拥有数组“快速访问”的特性，以及在查找元素过程中具有<`任意类型`>到`<任意类型>`的映射关系，哈希表就应运而生了。哈希表主要由**哈希函数** 和 **哈希冲突处理方法**两部分组成，其中**哈希函数**完成<`任意类型`>到`<int>`的映射（这儿用key-value来说明，key为输入，value为输出，即key到value的映射），但是这种映射关系并不唯一，即不同的key可能会有相同的value存在，若直接通过value来标记key的话，就会有覆盖现象发生，此时就会用到 **哈希冲突处理方法**。简单来讲，哈希表（Hash table，也叫散列表），是通过哈希函数将任意类型的数据转化成一个整型数字，然后用这个整型数字对数组长度取余，将其结果作为数组的下标，然后把这组数据存储到对应下标的数组空间（**数据存储过程**）。在使用哈希表进行数据查询时，就是再次通过哈希函数获取数组的下标，然后使用这个下标直接访问对应位置的数组元素，故哈希表查找数据的时间复杂度几乎为O(1)（**数据查找过程**）。

• 什么是哈希表（散列表）

  哈希表就是通过哈希函数将输入映射到数组的某个位置，然后利用数组的“随机访问”特性进行快速查找；通过哈希函数映射值来存放数据的数组就是哈希表。

• 为什么要使用哈希表

  在几乎为O(1)的时间复杂度内快速查找元素在数组中的位置。与一般查找不同，若直接在数组内查找某个元素，需要从头遍历一次数组，其时间复杂度为O(n)；若使用二分查找，每次都需要将待查找区间缩小一半，其时间复杂度为O(logn)；

• 哈希表、数组、链表的区别

  为了具有数组“随机访问”的特性，在哈希表中引入了哈希函数，然而哈希函数的引入会出现哈希冲突，比如“如果两个字符串在哈希表中对应的位置相同怎么办？”，而数组的容量又是有限的，其中一种解决方案就是使用链表结构，在哈希表的每个入口挂一个链表，保存所有对应的字符串就OK了，此时的哈希表就是一种数组+链表组合的数据结构。

3.2 哈希（散列）函数

把任意长度的输入（又叫做预映射， pre-image），通过散列算法，变换成固定长度的输出，该输出就是散列值。这种转换是一种压缩映射，也就是，散列值的空间通常远小于输入的空间，不同的输入可能会散列成相同的输出，而不可能从散列值来唯一的确定输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。

3.3 冲突处理方法

• 开放定值
• 再哈希|散列
• 拉链法
• 建立公共溢出区

哈希hash（散列）表结构详解_hash的结构-CSDN博客

Hash算法_bkdrhash acm-CSDN博客

3.4 代码演示

// 哈希函数：BKDRHash, 将 字符串类型 -> int
// 冲突处理：拉链法typedef struct Node {char *str;struct Node *next;
} Node;typedef struct HashTable {Node **data;int size;
} HashTable;Node *init_Node(char *str, Node *head) {Node *p = (Node *)malloc(sizeof(Node));p->str = strdup(str); // 深拷贝p->next = head;       // 头插法return p;
}HashTable *init_hash(int n) {HashTable *h = (HashTable *)malloc(sizeof(HashTable));h->size = n << 1; // 哈希表的空间利用率，一般为70%~90%，当前利用率为50%h->data = (Node **)calloc(h->size, sizeof(Node *));return h;
}int BKDRHash(char *str) {int seed = 31, hash = 0;for (int i = 0; str[i]; i++) hash = hash * seed + str[i];return hash & 0x7fffffff;
}int insert(HashTable *h, char *str) {int hash = BKDRHash(str);int ind = hash % h->size;h->data[ind] = init_Node(str, h->data[ind]);  // 拉链法return 1;
}int search(HashTable *h, char *str) {int hash = BKDRHash(str);int ind = hash % h->size;Node *p = h->data[ind];while (p && strcmp(p->str, str)) p = p->next;return p != NULL;
}void clear_node(Node *head) {if (head == NULL) return ;Node *p = head, *q;while (p != NULL) {q = p->next;free(p->str);free(p);p = q;}return ;
}void clear(HashTable *h) {if (h == NULL) return;for (int i = 0; i < h->size; i++) {clear_node(h->data[i]);}free(h->data);free(h);return ;
}