---

1. 递归的概念

简单的说: 递归就是方法自己调用自己，每次调用时传入不同的变量。递归有助于编程者解决复杂的问题，同时可以让代码变得简洁。

递归调用机制： 列举两个小案例，来帮助理解递归。

（1）打印问题

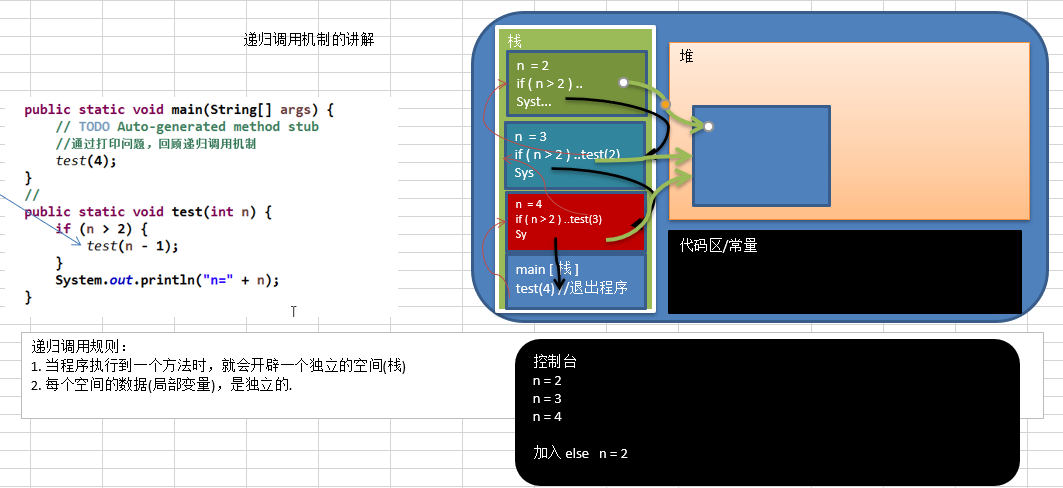
代码：

package recursion;public class RecursionTest {public static void main(String[] args) {test(4);}public static void test(int n) {if (n > 2) {test(n - 1);}System.out.println("n=" + n);}
}

（2）阶乘问题

package recursion;public class RecursionTest {public static void main(String[] args) {int res =factorial(3);System.out.println("res=" + res);}// 阶乘问题public static int factorial(int n) {if (n == 1) {return 1;} else {return factorial(n - 1) * n; // 1 * 2 * 3}}
}

运行结果：

2. 递归能解决什么问题

递归用于解决什么样的问题：
（1）各种数学问题如: 8 皇后问题 , 汉诺塔, 阶乘问题, 迷宫问题, 球和篮子的问题(google 编程大赛)
（2）各种算法中也会使用到递归，比如快排，归并排序，二分查找，分治算法等.
（3）将用栈解决的问题–>第归代码比较简洁

3. 递归的规则

递归需要遵守的重要规则：

1. 执行一个方法时，就创建一个新的受保护的独立空间(栈空间)
2. 方法的局部变量是独立的，不会相互影响, 比如 n 变量
3. 如果方法中使用的是引用类型变量(比如数组)，就会共享该引用类型的数据.
4. 递归必须向退出递归的条件逼近，否则就是无限递归,出现 StackOverflowError，死归了
5. 当一个方法执行完毕，或者遇到 return，就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或者返回时，该方法也就执行完毕。

4. 递归实际应用案例

4.1. 迷宫问题

    

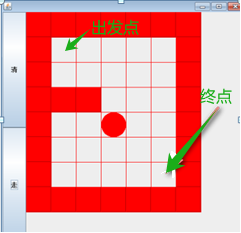
说明:
    小球得到的路径，和程序员设置的找路策略有关即：找路的上下左右的顺序相关
    在得到小球路径时，可以先使用(下右上左)，再改成(上右下左)，看看路径是不是有变化
    测试回溯现象

代码实现：

路径策略：下 --> 右 --> 上 --> 左

package recursion;public class MiGong {public static void main(String[] args) {//先创建一个二维数组，模拟迷宫//地图int[][] map = new int[8][7];//使用1表示墙//上下全部置为1for(int i = 0; i < 7; i++){map[0][i] = 1;map[7][i] = 1;}//设置挡板，1 表示map[3][1] = 1;map[3][2] = 1;//左右全部置为1for(int i = 0; i < 8; i++){map[i][0] = 1;map[i][6] = 1;}//输出地图System.out.println("地图的情况");for(int i = 0; i < 8; i++){for(int j= 0; j < 7; j++){System.out.print(map[i][j] + " ");}System.out.println();}//使用递归回溯给小球找路setWay(map, 1, 1);//输出新的地图，小球走过并标识过的地图的情况System.out.println("小球走过并标识过的 地图的情况");for(int i = 0; i < 8; i++){for(int j= 0; j < 7; j++){System.out.print(map[i][j] + " ");}System.out.println();}}// 使用递归回溯来给小球找路// 说明：// 1. map 表示地图// 2. i,j 表示地图的哪个位置开始出发（1,1）// 3. 如果小球能找到map[6][5] 位置，则说明通路找到// 4. 约定： 当map[i][j]为0 表示该点没有走过；当为1 表示墙；当为2表示通路（可以走）；当为3表示该位置已经走过，但是走不通// 5. 在走迷宫时，需要确定一个策略：下->右->上->左，如果该点走不通再回溯/*** * @param map 表示地图* @param i   表示从哪个行位置开始找* @param j   表示从哪个列位置开始找* @return 如果找到通路，就返回true，否则返回false*/public static boolean setWay(int[][] map, int i, int j) {if (map[6][5] == 2) {// 通路已经找到return true;} else {if (map[i][j] == 0) {// 当前这个点还没有走过// 按照策略走：下->右->上->左map[i][j] = 2;// 假定该点是可以走通if (setWay(map, i + 1, j)) {// 向下走return true;} else if (setWay(map, i, j + 1)) {// 向右走return true;} else if (setWay(map, i - 1, j)) {// 向上走return true;} else if (setWay(map, i, j - 1)) {// 向左走return true;} else {// 说明该点是走不通的，是死路map[i][j] = 3;return false;}} else {// 如果map[i][j] != 0, 可能是1（墙）,2（走过了）,3（死路）return false;}}}
}

运行结果：

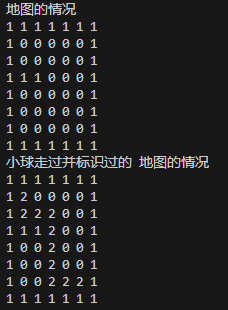
思考: 如何求出最短路径?

4.2. 八皇后问题

    
问题：

    八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848 年提出：在 8×8 格的国际象棋上摆放八个皇后，使其不能互相攻击，即：任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法(92)。

4.2.1. 思路分析

    ①第一个皇后先放第一行第一列
    ②第二个皇后放在第二行第一列、然后判断是否 OK， 如果不 OK，继续放在第二列、第三列、依次把所有列都放完，找到一个合适
    ③继续第三个皇后，还是第一列、第二列……直到第 8 个皇后也能放在一个不冲突的位置，算是找到了一个正确解
    ④当得到一个正确解时，在栈回退到上一个栈时，就会开始回溯，即将第一个皇后，放到第一列的所有正确解，全部得到
    ⑤然后回头继续第一个皇后放第二列，后面继续循环执行 1,2,3,4 的步骤
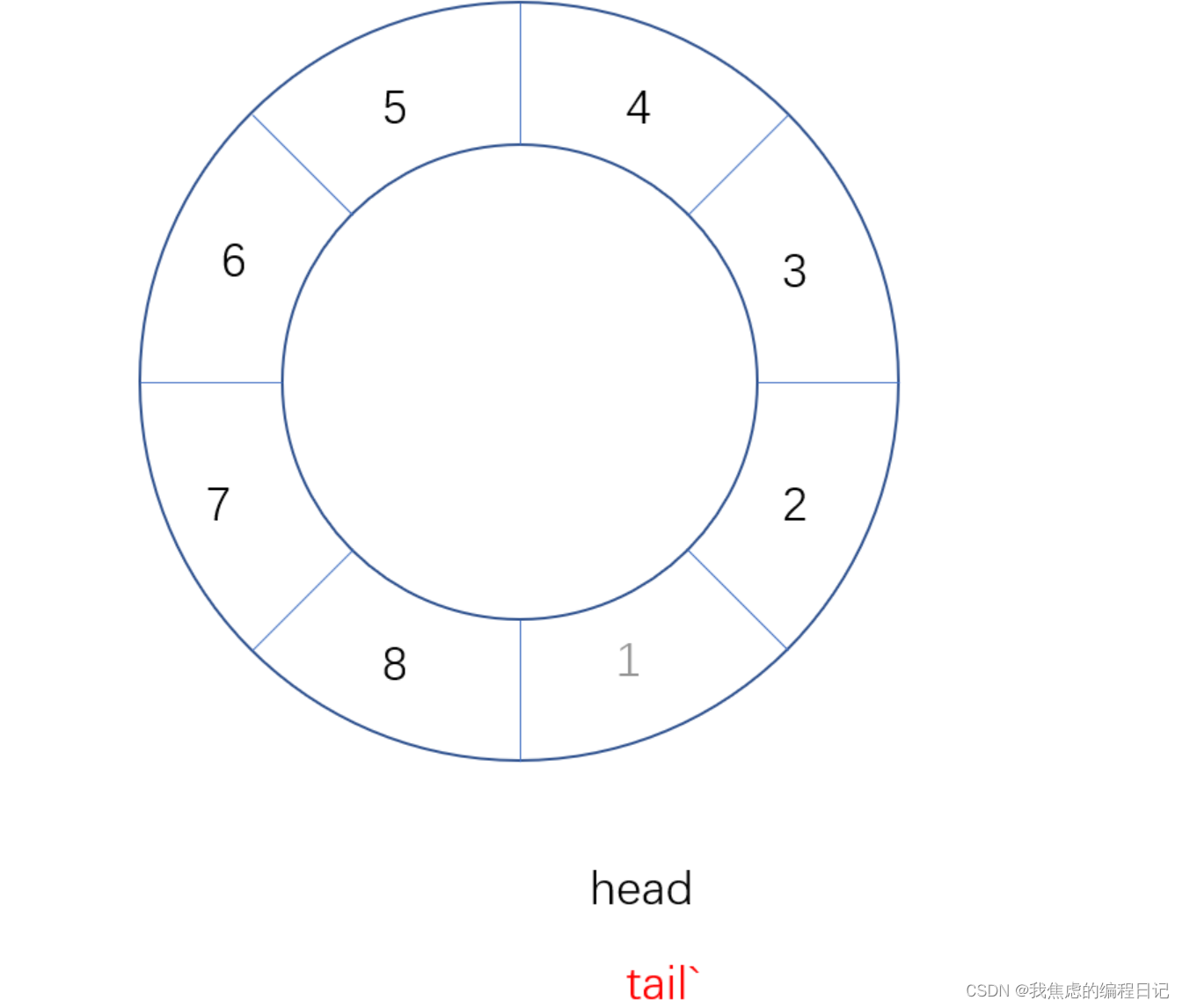
示意图:

说明：
    理论上应该创建一个二维数组来表示棋盘，但是实际上可以通过算法，用一个一维数组即可解决问题。arr[8] ={0 , 4, 7, 5, 2, 6, 1, 3} //对应 arr 下标 表示第几行，即第几个皇后，arr[i] = val , val 表示第 i+1 个皇后，放在第 i+1 行的第 val+1 列

4.2.1. 代码实现

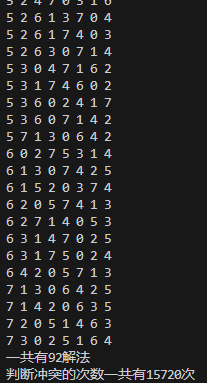
package recursion;public class Queue8 {// 定义一个max表示共有多少个皇后int max = 8;// 定义数组array，保存皇后放置位置的结果，比如arr = {0, 4, 7, 5, 2, 6, 1, 3}int[] array = new int[max];static int count = 0;static int judgeCount = 0;public static void main(String[] args) {Queue8 queue8 = new Queue8();queue8.check(0);System.out.printf("一共有%d解法\n", count);System.out.printf("判断冲突的次数一共有%d次", judgeCount);}// 编写一个方法，放置第n个皇后// 特别注意：check 是每一次递归时，进入到check中都有 for(int i = 0; i < max; i++),因此会有回溯private void check(int n) {if (n == max) {// n=8时，8个皇后就已经放好了print();return;}// 依次放入皇后，并判断是否冲突for (int i = 0; i < max; i++) {// 先把当前这个皇后n，放到该行的第1列array[n] = i;// 判断当放置第n个皇后到i列时，是否冲突if (judge(n)) {// 不冲突// 接着放n+1个皇后，即开始递归check(n + 1);}// 如果冲突，就继续执行上面代码（array[n] = i）；即将第n个皇后放置在本行的后移一个位置}}// 查看，当我们放置第n个皇后，就去检测该皇后是否和前面已经摆放的皇后冲突/*** * @param n 表示第n个皇后* @return*/private boolean judge(int n) {judgeCount++;for (int i = 0; i < n; i++) {// 说明// 1. array[i] == array[n] 表示判断：第n个皇后是否和前面的n-1个皇后在同一列// 2. Math.abs(n-i) == Math.abs(array[n] - array[i])：表示判断第n个皇后和第i皇后是否在同一斜线// 3. 判断是否在同一行：没有必要，n每次都在递增if (array[i] == array[n] || Math.abs(n - i) == Math.abs(array[n] - array[i])) {return false;}}return true;}// 写一个方法，可以将皇后摆放的位置输出private void print() {count++;for (int i = 0; i < array.length; i++) {System.out.print(array[i] + " ");}System.out.println();}}

运行结果：