scipy
- 是什么
- 常用方法
是什么
scipy是Python语言的一个开源数值计算库,主要目的是为科学、工程、计算等领域提供有用的数学算法和函数,包括线性代数、优化、信号处理、傅里叶变换、统计函数等。它是Python科学计算环境的重要组成部分,通常与NumPy和Matplotlib等库一起使用。
常用方法
- 线性代数:scipy.linalg
- solve:解线性方程组
- det:计算矩阵的行列式
- eig:计算矩阵的特征值和特征向量
- inv:计算矩阵的逆矩阵
- svd:计算矩阵的奇异值分解
import numpy as np
from scipy import linalg# 创建一个2x2的矩阵
A = np.array([[1, 2], [3, 4]])# 计算矩阵的行列式
det_A = linalg.det(A)
print("det(A) =", det_A)# 计算矩阵的逆矩阵
inv_A = linalg.inv(A)
print("inv(A) =\n", inv_A)# 解线性方程组 Ax = b
b = np.array([5, 6])
x = linalg.solve(A, b)
print("x =", x)# 计算矩阵的奇异值分解
U, s, V = linalg.svd(A)
print("U =\n", U)
print("s =", s)
print("V =\n", V)结果
det(A) = -2.0
inv(A) =[[-2. 1. ][ 1.5 -0.5]]
x = [-4. 4.5]
U =[[-0.40455358 -0.9145143 ][-0.9145143 0.40455358]]
s = [5.4649857 0.36596619]
V =[[-0.57604844 -0.81741556][ 0.81741556 -0.57604844]]- 优化:scipy.optimize
- minimize:对一个目标函数进行最小化
- root:求解方程组
- curve_fit:拟合数据曲线
- minimize_scalar:对一个一元函数进行最小化
import numpy as np
from scipy import optimize# 定义需要最小化的函数
def f(x):return x ** 2 - 4 * x + 3# 使用Brent算法求取函数的最小值
result = optimize.minimize_scalar(f, method="brent")
print("minimum value: ", result.fun)
print("minimum point: ", result.x)结果
minimum value: 1.0
minimum point: 2.0import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt# 构造正弦函数
def sin_func(x, a, b, c, d):return a * np.sin(b * x + c) + d# 构造数据
x_data = np.linspace(0, 2 * np.pi, 50)
y_data = sin_func(x_data, 3, 1.5, np.pi / 3, 2) + 0.5 * np.random.normal(size=len(x_data))# 使用curve_fit拟合数据
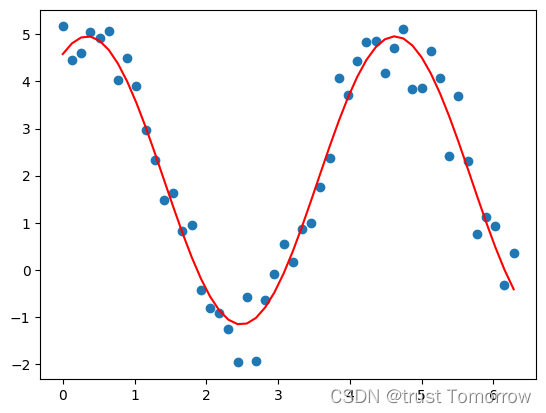
popt, pcov = curve_fit(sin_func, x_data, y_data)# 绘制原始数据和拟合结果
plt.scatter(x_data, y_data, label='Original data')
plt.plot(x_data, sin_func(x_data, *popt), 'r-', label='Fit result
from scipy.optimize import root
import numpy as np# 定义方程
def func(x):return x**2 + 2*np.sin(x)# 求解方程的根
sol = root(func, 0.3)# 输出结果
print(sol.x) # [0.]from scipy.optimize import root
import numpy as np# 定义方程组
def func(x):return [x[0]**2 + x[1]**2 - 1, x[0] + x[1] - np.sqrt(2)]# 求解方程组的根
sol = root(func, [1, 1])# 输出结果
print(sol.x)
# [0.70710679 0.70710678]from scipy.optimize import minimize
import numpy as np# 定义目标函数
def rosen(x):"""Rosenbrock函数"""return sum(100.0 * (x[1:] - x[:-1]**2.0)**2.0 + (1 - x[:-1])**2.0)# 定义约束条件
cons = ({'type': 'ineq', 'fun': lambda x: x[0] - 1},{'type': 'ineq', 'fun': lambda x: -x[0] - 1},{'type': 'ineq', 'fun': lambda x: x[1] - 1},{'type': 'ineq', 'fun': lambda x: -x[1] - 1})# 求解最小值
x0 = np.array([0, 0])
res = minimize(rosen, x0, method='SLSQP', constraints=cons)# 输出结果
print(res)
"""message: Positive directional derivative for linesearchsuccess: Falsestatus: 8fun: 0.9999999999965967x: [ 1.702e-12 1.692e-14]nit: 8jac: [-2.000e+00 1.490e-06]nfev: 42njev: 4
"""- 插值:scipy.interpolate
- interp1d:一维插值
- interp2d:二维插值
- griddata:多维插值
import numpy as np
from scipy.interpolate import interp1d
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 创建一些随机数据点
x = np.linspace(0, 10, 10)
y = np.sin(x)# 使用线性插值生成更多的数据点
f_linear = interp1d(x, y, kind='linear')
x_new = np.linspace(0, 10, 30)
y_linear = f_linear(x_new)# 使用样条插值生成更多的数据点
f_cubic = interp1d(x, y, kind='cubic')
y_cubic = f_cubic(x_new)# 绘制原始数据和插值曲线
plt.plot(x, y, 'o', label='原始数据点')
plt.plot(x_new, y_linear, '-', label='线性插值')
plt.plot(x_new, y_cubic, '--', label='样条插值')
plt.legend()
plt.show()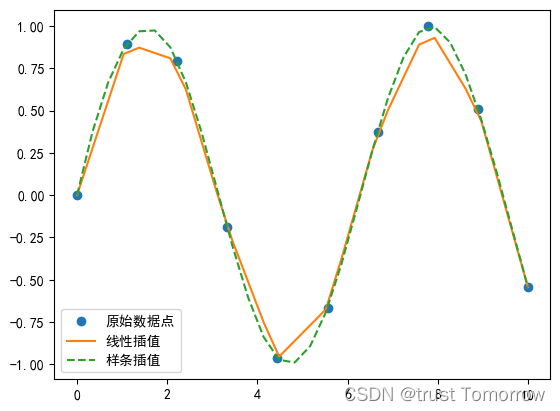
- 信号处理:scipy.signal
- fft:快速傅里叶变换
- convolve:卷积运算
- resample:重新采样
- spectrogram:信号的谱分析
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt# 生成一个带噪声的信号
t = np.linspace(0, 10, 1000)
y = np.sin(t) + np.random.normal(0, 0.1, t.shape)# 设计一个低通滤波器并应用于信号
b, a = signal.butter(4, 0.1, 'low') # 4 表示滤波器阶数,0.1 表示截止频率
y_filtered = signal.filtfilt(b, a, y) # Filtfilt 函数应用前向和反向滤波器,可以减少滤波器导致的相位延迟# 绘制原始信号和滤波后的信号
plt.figure(figsize=(6, 6))
plt.subplot(2, 1, 1)
plt.plot(t, y, label='原始信号')
plt.xlabel('时间')
plt.ylabel('幅度')
plt.legend()plt.subplot(2, 1, 2)
plt.plot(t, y_filtered, label='滤波后的信号')
plt.xlabel('时间')
plt.ylabel('幅度')
plt.legend()plt.show()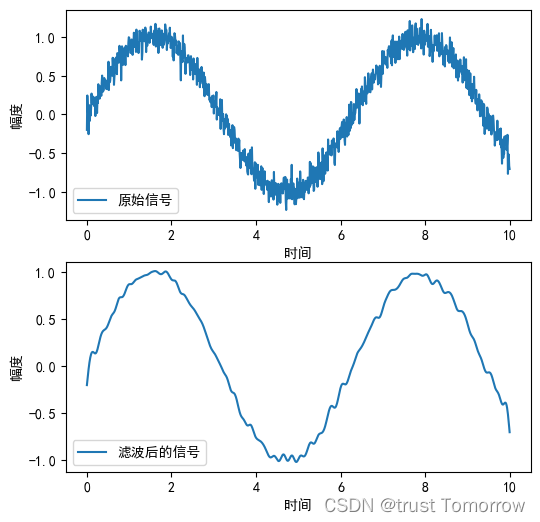
- 统计:scipy.stats
- ttest_ind:t检验
- pearsonr:计算Pearson相关系数
- chi2_contingency:卡方检验
- f_oneway:方差分析
import numpy as np
from scipy import stats
import matplotlib.pyplot as plt# 生成 1000 个随机变量
x = np.random.normal(0, 1, 1000)# 计算随机变量的均值和方差
mean = stats.mean(x)
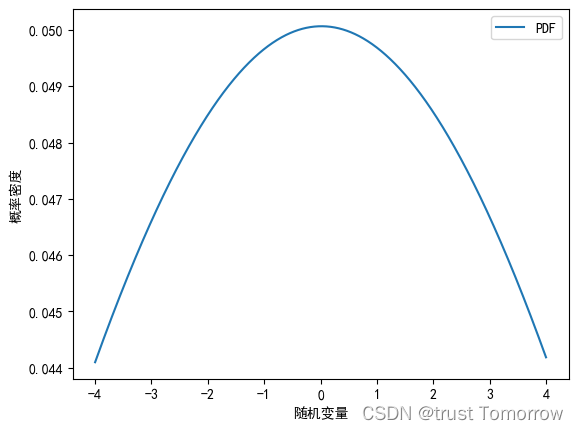
variance = stats.variation(x)# 计算随机变量的概率密度函数(PDF)并绘制出来
pdf_x = np.linspace(-4, 4, 1000)
pdf_y = stats.norm.pdf(pdf_x, loc=mean, scale=np.sqrt(variance))plt.plot(pdf_x, pdf_y, label='PDF')
plt.xlabel('随机变量')
plt.ylabel('概率密度')
plt.legend()
plt.show()