在结构光三维重建中,通过相移法求解出来的相位是包裹相位(在 [-π/2,π/2] 间成周期性 )
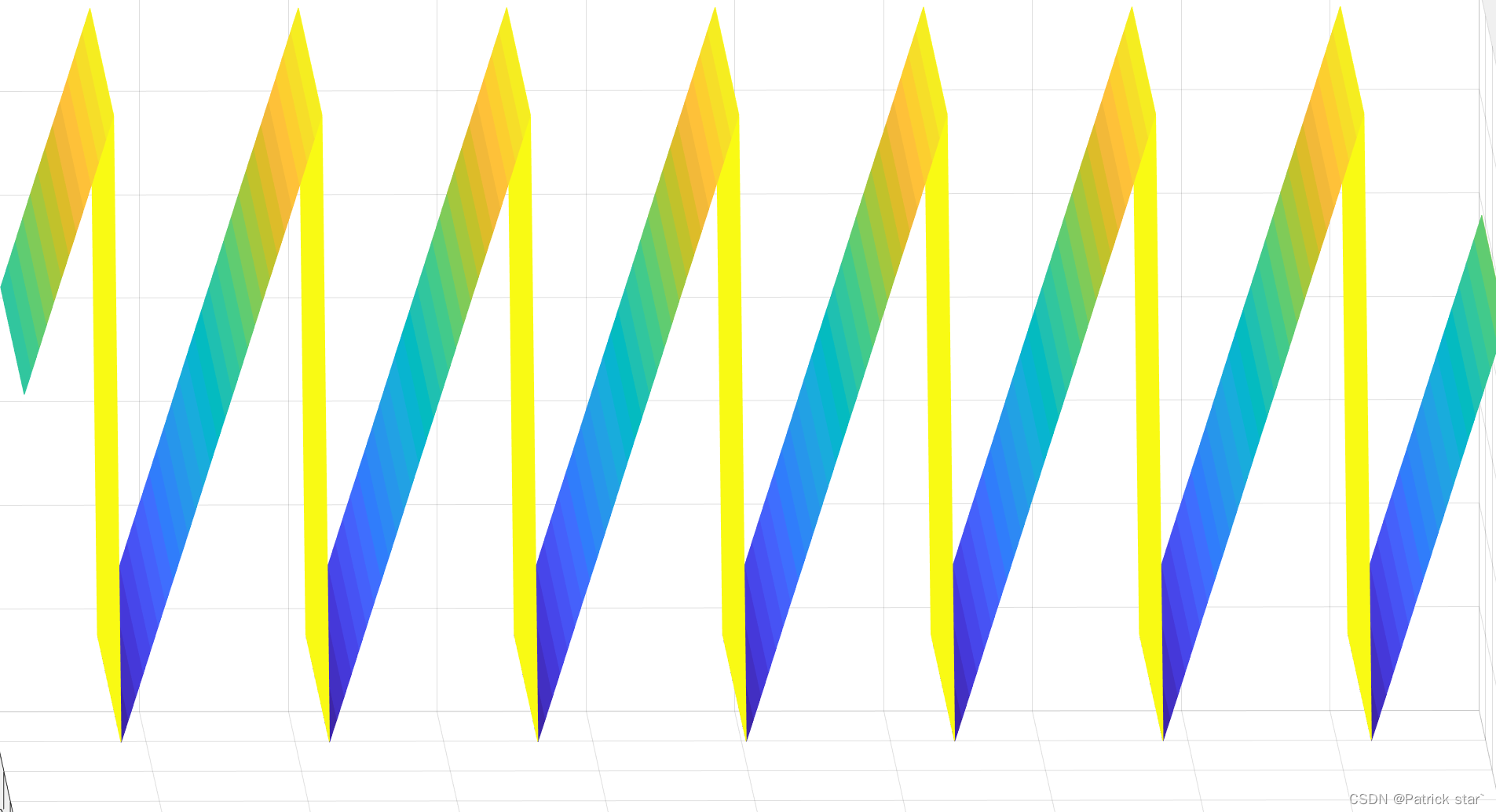
我们想要用相位找到相机与投影仪间的对应像素,就需要进行相位展开,确保每一行的相位值是唯一的。
多频外差是相位展开的一种,接下来我们会介绍它的原理,以及代码。
多频外差的原理是将两种不同频率的相位函数叠加得到一个频率更低的相位函数,设对应的周期分别是
是
合成的相位

利用求解阶次
如果求取的阶次:
如何理解这个公式?
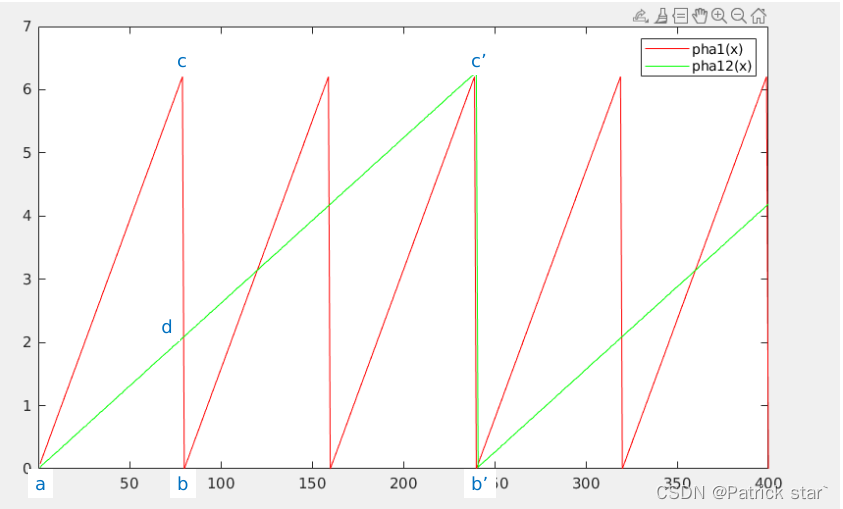
之后,
会重合
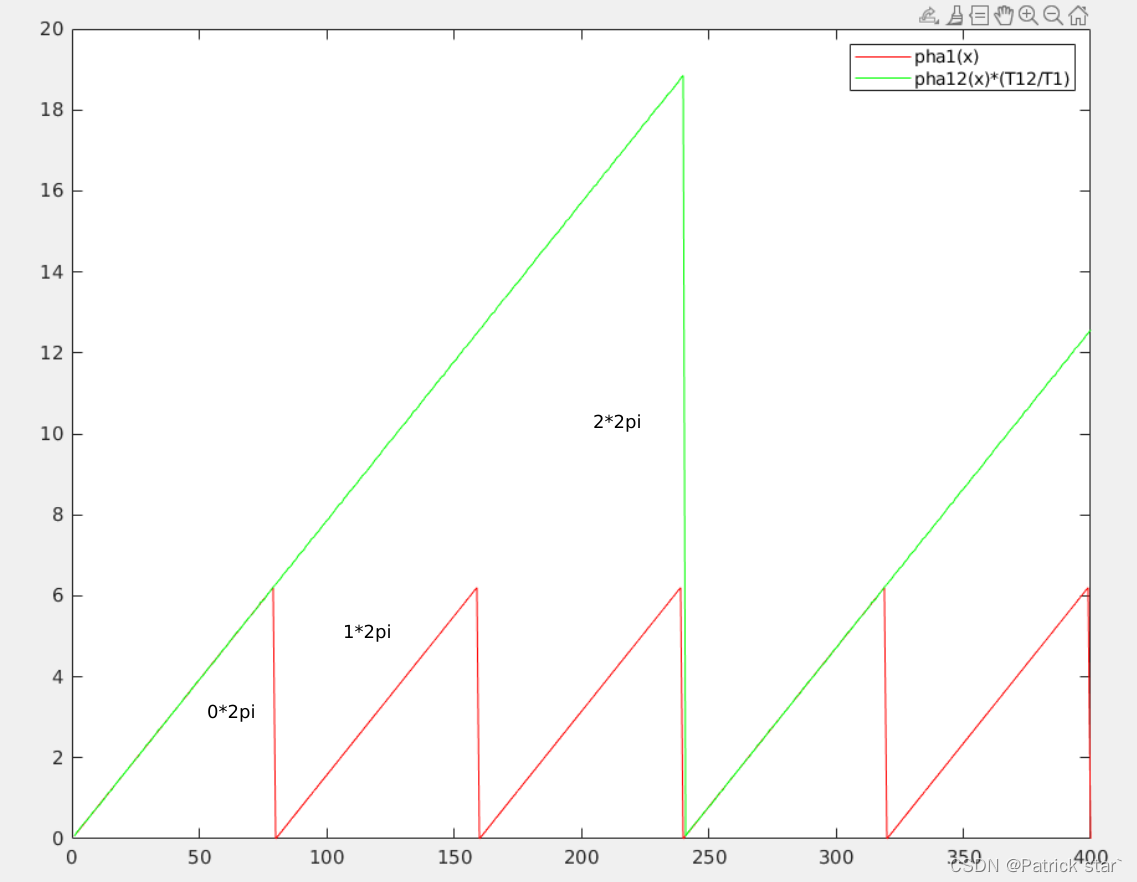
就能得到
的阶次
最后就可以求出绝对相位
(k是求得的阶次)