问题背景

KMP算法主要应用与字符串的比较，有一个主串，有一个子串，我们要通过一种方式来查看子串是否为主串的一部分。我们通常的想法是：主串和子串左对齐，一个字符一个字符进行比较，如果其中有个字符不匹配的话，那么主串不同，子串向右移动一个范围。这样不断循环，直到找到一个完整的匹配的子串。但如果这样做的话，无疑时间复杂度是最高的，时间复杂度是mn。那有没有更快的方式呢？KMP算法的特点就是一个快速，能够在这种情况下快速地找到一个匹配的子串。

KMP算法是什么呢？

KMP算法操作呢？这个时候就要引入一个公共前后缀和最大公共前后缀的概念，比如这样的一串字符“A B A B A B” 这样的一串字符有很多公共的前后缀，AB是一个ABAB也是一个，甚至没有限制的话ABABAB也能算一个。那最大公共前后缀呢？这里我们的最大公共前后缀实际上有一个限制，那就是小于自身长度的最大公共前后缀，这个时候的最大公共前后缀就是ABAB了。知道这个有什么用呢？我们知道在傻瓜式的比较方式中，每次比较完了之后，子串不仅要向右移动，其中代表子串数组下标用于移动的变量，我们暂且称之为指针（虽然不是真正意义上的），这个指针是需要回溯的，也就是回到子串的首部进行重新比较。这个时候我们就有一个让指针保持在原地的方式，那就是让子串移动到的公共前缀和公共后缀重叠的地方来，然后在指针的位置进行比较。那有些人会有疑惑：那你这样移动那么多位数的话，那中间是不是错过了匹配的情况呢？事实上是不会的，如果错过了，那一定是公共前后缀选择小了，即找的那个并不是真正的公共前后缀。这个点就是这个KMP算法的核心，也就是这个算法的神奇之处。如果不太理解，记住即可，这个就是事实。

next数组

很好，我们有了基本的操作方式，可以高效率地判断这个子串是否是这个主串中的一部分了。如果我们止步于此，那么我们就只能手工地进行一些简单的判断，但是进入到代码层面，要考虑的事情还有很多。

首先我们面对的是各式各样的比较，在我们拿到一个主串和一个子串的时候，我们是不能预先知道这个子串在和主串比较的时候在那个元素上发生故障的，所以我们在操作的时候，每次都得计算最大公共前后缀是那个，然后才能移动，那有没有可能将这个过程封装起来，类似于一个函数，我们首先假设每一个位置都会失败（因为运行之前我们不知道哪个会失败，所以只能假设全都失败），然后进而求出他们的公共前后缀（公共前后缀只需要知道子串就好了），然后再计算他们移动的位数，这样的话，在真正的执行的过程中，那个位置比较失败了，就调用相关的函数将其中的移动的步数求出来，但是落实到代码当中，内存是不是真正移动的，所以只能是指针移动到子串的那个位置和此时出错的主串元素进行比较，这样话就转化成，某个位置失败了，我们就直接可以知道接下来那个子串的位置和我这个主串的位置进行比较了。那我们还可不可以将这个方式再优化一下，我们能不能提前执行这个函数，将这个位置结果存在一个固定的地方，下次直接调用就好了？是的，这个就是next数组！表示的就是，当某个位置失败的时候，那我们可以通过这个位置的下标访问这个数组，取到这个数组里面的值，这个值就是我们子串中下次和主串相比较的位置下标。

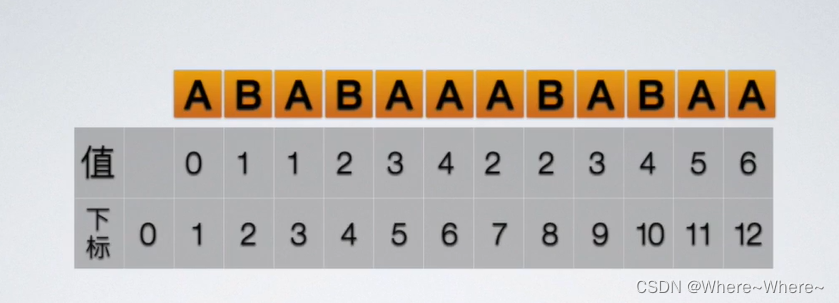
其中的next数组下表是从1开始的，下表0里面是不存东西的。next数组里面的值0表示的就是子串的第一个和主串失败位置的下一个进行比较。 

next数组的代码实现细节

既然有了实现next数组的思路，那具体的代码怎么实现呢？实现的时候要注意什么呢？如果我们以遍历的方式来求next数组的话，那么具体的过程是这样的：对于每一个子串失败的位置，我们都需要用两个指针在失败位置前的全部部分，一左一右进行扫描，跳出循环的条件是右边到达了最左边，左边到达了最右边，同时两个指针指向的内容进行比较，如果相同的话，继续走，同时计算个数c，如果不对的话跳出循环，这个时候第 c +1个子串的上的元素就要和主串上的元素进行比较，这样的下来的话，要走n趟，每一趟的复杂度也是n，总的来说的是n^2，这样的话就和不采用next数组的傻瓜方式的时间复杂度就是一样的了。那能不能优化呢？

我们在从子串的第一个元素到最后一个元素都在计算Next数组的值，值也是算一个放一个，那算后续Next的值的时候，能不能使用之前已经计算过的Next的值呢？答案是可以的。我们观察上一个部分的next数组的部分的时候，就发现了这样的一个规律：我们next数组中存的其实就是最大公共前后缀 + 1 后的数值，这个很重要！比如我们计算了第n个位置的next数组的值之后，想要计算n + 1个位置上的Next数组上的值，怎么计算呢？这个时候就得看最大公共前后缀！如果我们发现，子串中n上的值和n的失败过后找到的位置t上面的值是相同的话，那么这就意味着，子串上的第 n+ 1 个元素的最大公共前缀是比n的多一个的，这不就意味着，n + 1 在next数组中的值是 n在next数组中的值 + 1吗；如果不相等的话，这就有趣了，看下图！

如果不相等的话，这不就回到我们问题的初始阶段吗，可以将上述的子串看做是主串，下面的子串就是比较的子串。因为我们现在求得是最大公共前后缀，只需要子串就好了，不需要主串，因为我们求最大公共前后缀的前提就是假设某一个元素的失败的，已经过了和主串比较的阶段，所以这里只讨论子串。这个时候Pt和Pj（这里的j就是上述说的n）比较失败，那我们就得寻找子串 t 位置上的公共前后缀，我们有吗？肯定是有的，我们都讨论到了子串j上的Next数组的值，那小于j的t上的值是一定有的，这个时候直接查next数组就好了，然后再将这个值赋值和t，也就是t = next[t]，有些人看这个代码有点不明白，是的，初看的时候确实有点模糊，心里想为什么不换一个变量名字区分一下呢？其实这样做也是为了重复利用变量t这部分的空间，如果还看不明白，就只要记住赋值号的结合性是从右向左的，而不是从左向右的，这就是为什么很疑惑的原因了，只要搞清楚了语法的具体执行步骤，先取出t所在next数组里面的值，再赋值给t，覆盖掉之前在t中的值，这个时候t就是一个新的t了，这样就不会疑惑了。这样不断寻找的话，只要找到了新的t中的值是和原来的j所在的值是相同的，那么 子串中j + 1所在位置失败的时候，寻找的位置就是 (新 t + 1)，如果到最后还是没有找到的话，也就是说找到了子串的第一个进行比较还是失败的话，注意这里很容易被绕进去，现在我们讨论的是公共前后缀的个数，我们现在是计算 j +1的公共前后缀的个数（不要和正式的主串和子串的比较产生混淆），现在正在用j + 1前面 j 的值和子串中第一个值进行比较，只有第一个值失败之后，我们再回到next数组里面的才会有 t = 0，当出现t = 0的时候，这就意味着连第一个位置都不和 Pj是相同的，那么这就代表着   j + 1前面的所有部分是没有公共前后缀的，即为0，所以当 第j +1 个位置失败之后，是需要第一个元素来个主串比较的，不管是next数组的规律公式层面，还是理解层面，这个时候 j + 1在next数组里面需要填写的值是 0 + 1 或者是1. 所以才会出现next[j + 1] = 1; 

值得注意的是，在整个next数组中，只有子串中第一个元素失败的时候，其中的next值才是0，其代表的意思是：子串的第一个元素和主串第n个位置比较失败，这个时候，子串中已经没有可以比较的元素了，所以主串和子串的匹配开头元素一定不是从这个元素开始的，所以接下来的策略是将子串想后移动一位，让子串的第一个元素和主串的第n + 1个元素进行比较。

有了next数组就够了吗？还可以优化吗？不太够，可以优化。如果我们出现这样的情况：