目录
原题描述:
题目描述
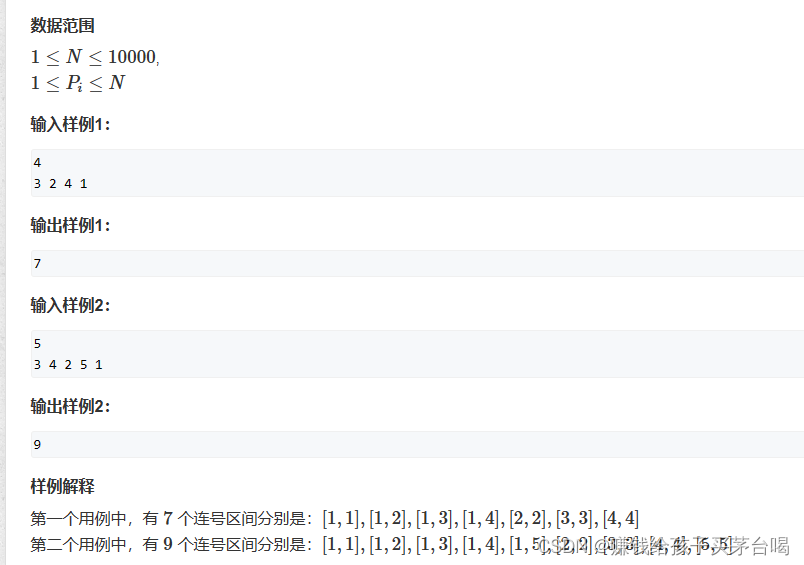
样例输入1
样例输出1
样例输入2
样例输出2
题目大意:
主要思路:
change的设计:
dp的转移:
dp初始化:
dp的结算:
注意事项:
代码(有注释):
原题描述:
题目描述
Alice 和 Bob 在玩游戏。
给出一个长度为偶数的,非空的且仅含小写字母的字符串。每个玩家还拥有一个初始为空的字符串。
Alice 先手,两名玩家交替行动。在一次行动中,玩家可以取 首或尾字符,将其从
中移除后加入到自己的字符串的 最前面。
当 为空时游戏结束,拥有字典序更小的字符串的玩家获胜。若两名玩家的字符串相等则平局。
若 Alice 和 Bob 都足够聪明,判断谁会取胜,或者游戏为平局。
数据组数,
。保证所有输入的
长度都为偶数。
样例输入1
1
aa
样例输出1
Draw
样例输入2
1
ab
样例输出2
Alice
题目大意:
给你一个字符串,每次玩家可以从左边或右边取走一个字符放在自己的最前边,两名玩家交替行动,问最后谁赢了,Alice赢了输出Alice,Bob赢了输出Bob,平局输出Draw。
主要思路:
这个题很难想,很难想到区间dp来做,即使想到了也未必写出来。
想到区间dp来做后,我们发现这个题的分割点再左或右,我们可以用0表示Alice赢,1表示平局,其他数表示Bob赢,我们先设计一个函数change(a,b,c),表示是谁赢,a代表是谁赢,b表示Alice选什么,c表示Bob选啥,dp[l][r]代表区间[l~r]是谁赢。
change的设计:
如果a不是平局的话,那么就应该从a转移过来,就return a,否则就返回选的谁大谁小。
dp的转移:
这个dp可以从四个地方转移:
v1=dp[l+1][r-1],Alice取l,Bob取r
v2=dp[l+2][r],Alice取l,Bob取l+1
v3=dp[l+1][r-1],Alice取r,Bob取l
v4=dp[l][r-2],Alice取r,Bob取r-1
dp初始化:
要初始化成Bob赢。
dp的结算:
由于Alice先手,所以最外层是min(也就是为啥Alice赢的数字是0)内层是max(Bob的赢)
等想到这些后就好写了。
注意事项:
- 当len=2时,如果两侧不相同,Alice必赢,否则平局。
代码(有注释):
#include<bits/stdc++.h>
using namespace std;
int dp[3010][3010];
char s[3010];
int change(int a,int b,int c)
{if(a!=1){return a;}return s[b]<s[c]?0:(s[b] == s[c]?1:2);//判断谁赢
}
int main()
{
// freopen("sample (42).in","r",stdin);int t;cin>>t;while(t--){cin>>s+1;int n=strlen(s+1);for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dp[i][j] = 3;//初始化 }}for(int len=2;len<=n;len+=2){for(int l=1;l+len-1<=n;l++){int r=l+len-1;if(len == 2){dp[l][r] = (s[l] == s[r]);continue;}int ret=2;ret = min(ret,max(change(dp[l+1][r-1],l,r),change(dp[l+2][r],l,l+1)));ret = min(ret,max(change(dp[l+1][r-1],r,l),change(dp[l][r-2],r,r-1)));//结算 dp[l][r] = ret;}}cout<<(dp[1][n]==0?"Alice\n":(dp[1][n]==1?"Draw\n":"Bob\n"));}return 0;
}