1.贝叶斯公式
![]()
贝叶斯理论的思路是,在主观判断的基础上,先估计一个值(先验概率),然后根据观察的新信息不断修正(可能性函数)。
P(A):没有数据B的支持下,A发生的概率,也叫做先验概率。这完全是根据经验做出的判断,这也是前面说的贝叶斯公式的主观因素部分。
P(A|B):在数据B的支持下,A发生的概率,也叫后验概率。即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A):给定某参数A的概率分布:也叫似然函数。这是一个调整因子,即新信息B带来的调整,作用是使得先验概率更接近真实概率。至于新信息带来的调整作用大不大,还得看因子的值大不大。
假如我在大学校园中随机找出一个人B,身高170,体重60。P(A)是大学中男生的占比,是先验概率。
那么从所有男生中选出身高170,体重60的人的概率就是似然概率,也就是从男生的分布(男生的概率密度函数)中得到B的概率。
那么选出的这个人B是男生的可能性就是后验概率P(A|B)。
无监督学习中的一个核心问题就是——密度估计问题。要训练出一个模型,使该模型的概率密度函数和真实的训练数据分布尽可能相似。
2.生成模型分类
无监督学习两种典型思路:
1.显式密度估计:显式的定义并求解分布Pmodel(x)。分布的方程是能够写出来定义出来的。可以算出特征空间中选取的点生成的样本可信度,概率值。
2.隐式的密度估计:学习一个模型Pmodel(x),无需显式的公式定义。只能够生成样本。只会产生特征空间中概率比较大,与真图相似的点。
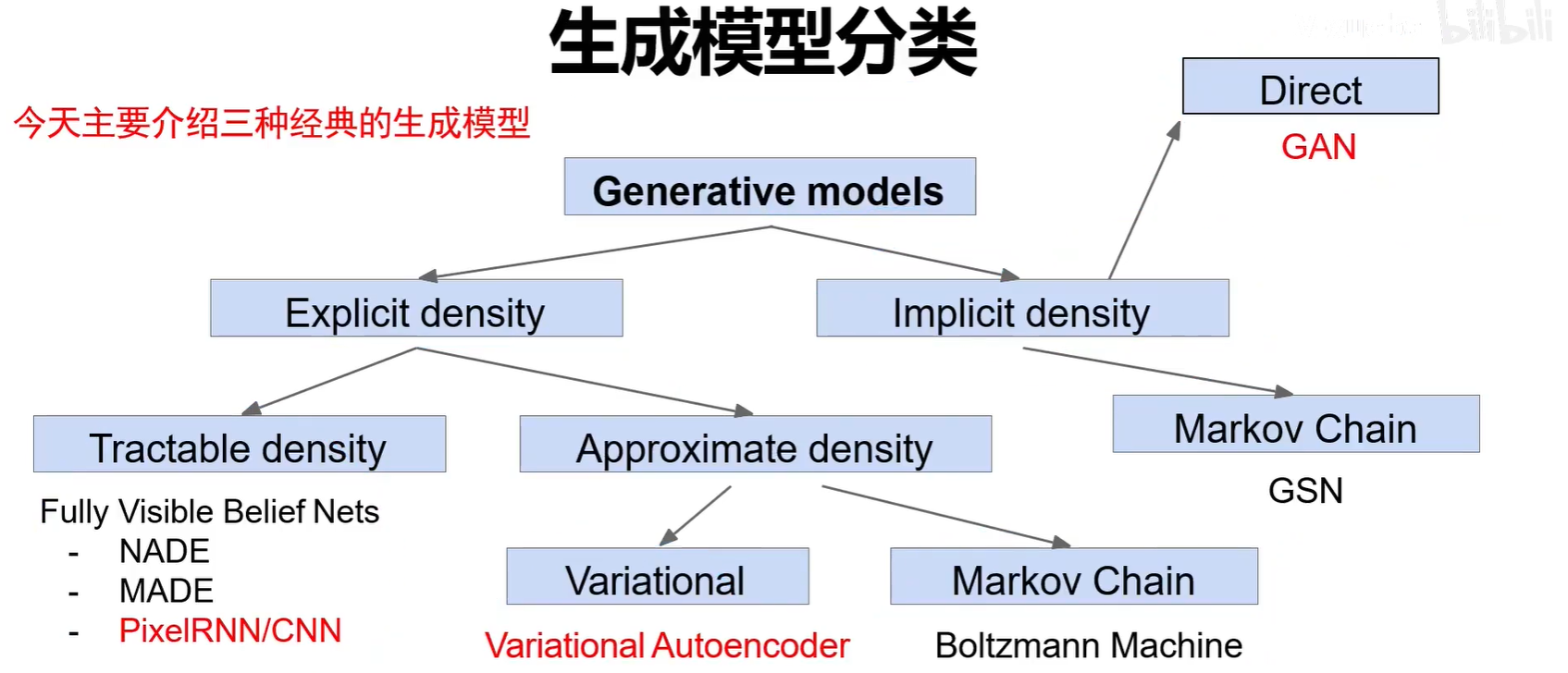
生成模型主要分为显示概率密度-可求解,显式概率密度-可近似和隐式概率密度。
2.1 PixelRNN与PixelCNN


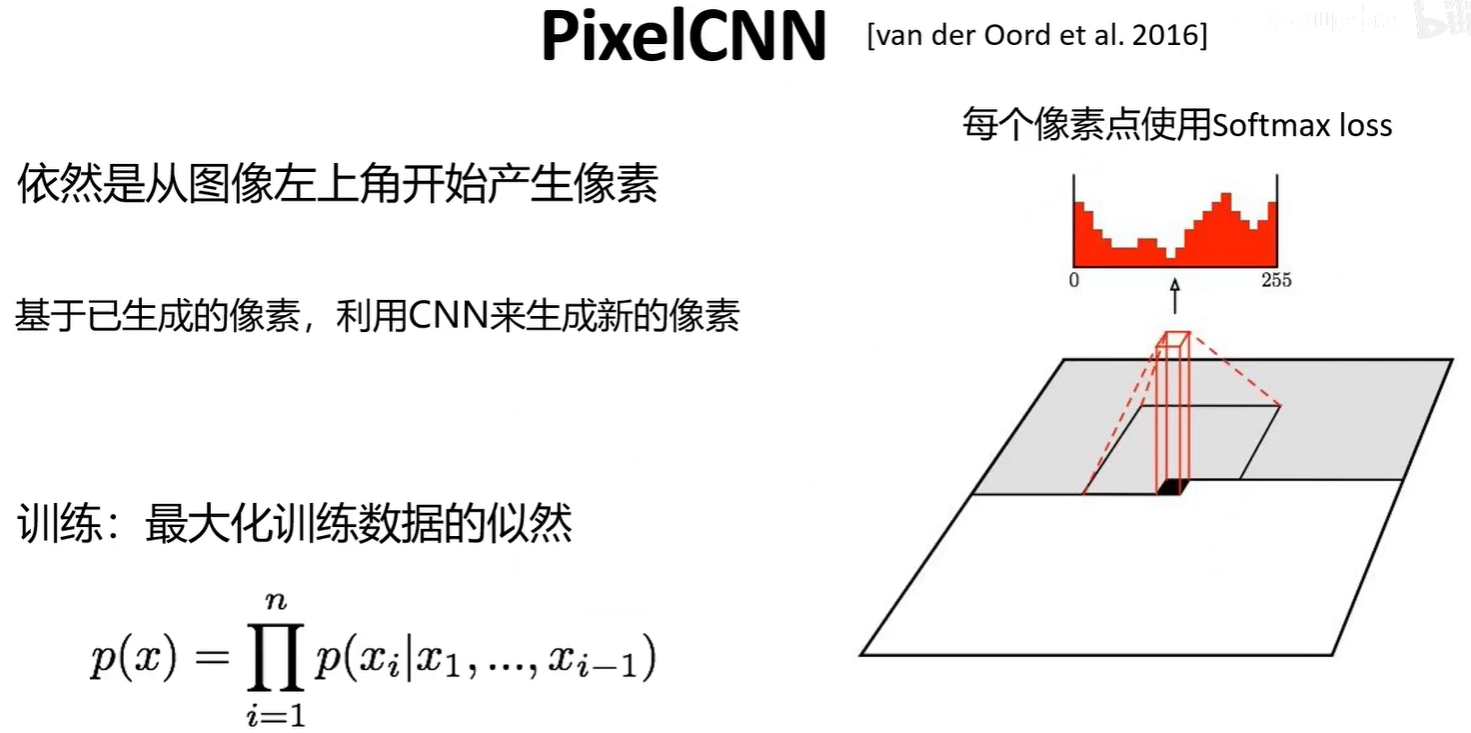

PixelRNN与PixelCNN是前面的像素生成后,来预测下一个像素的值,在知道前面的像素值后,该像素值的概率分布(0-255的每个值的概率)是可以计算出来的。
2.2 VAE
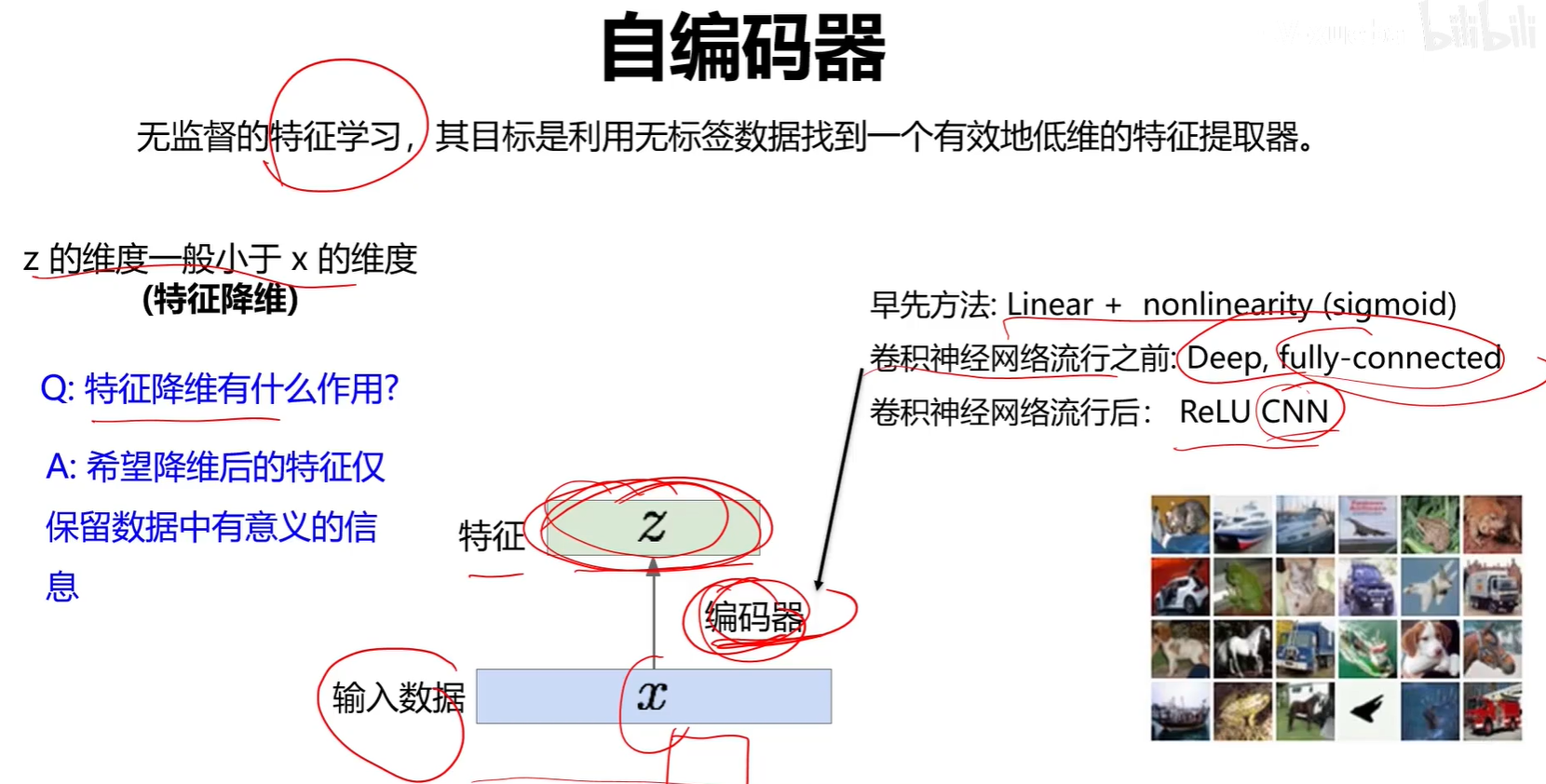
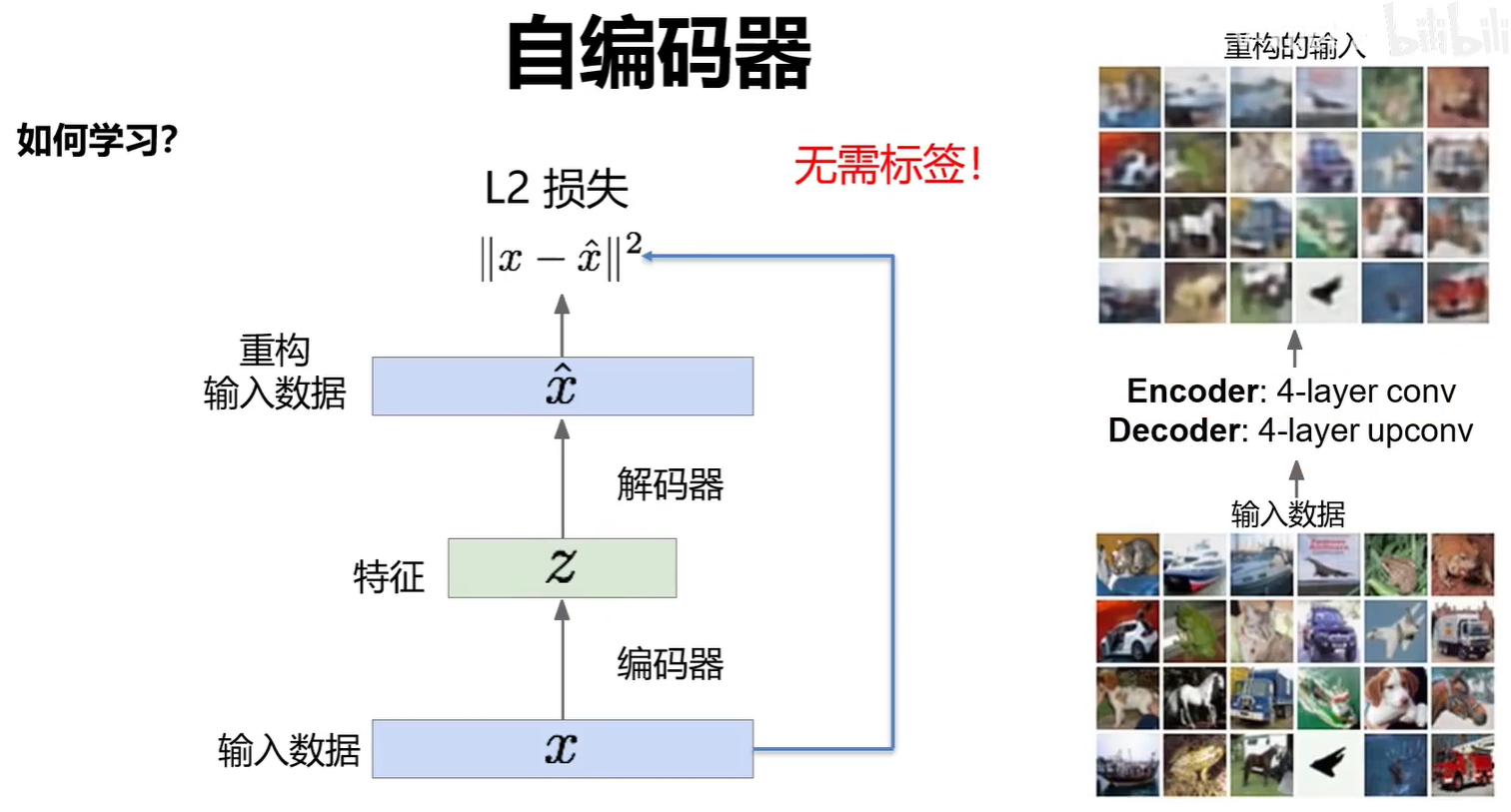
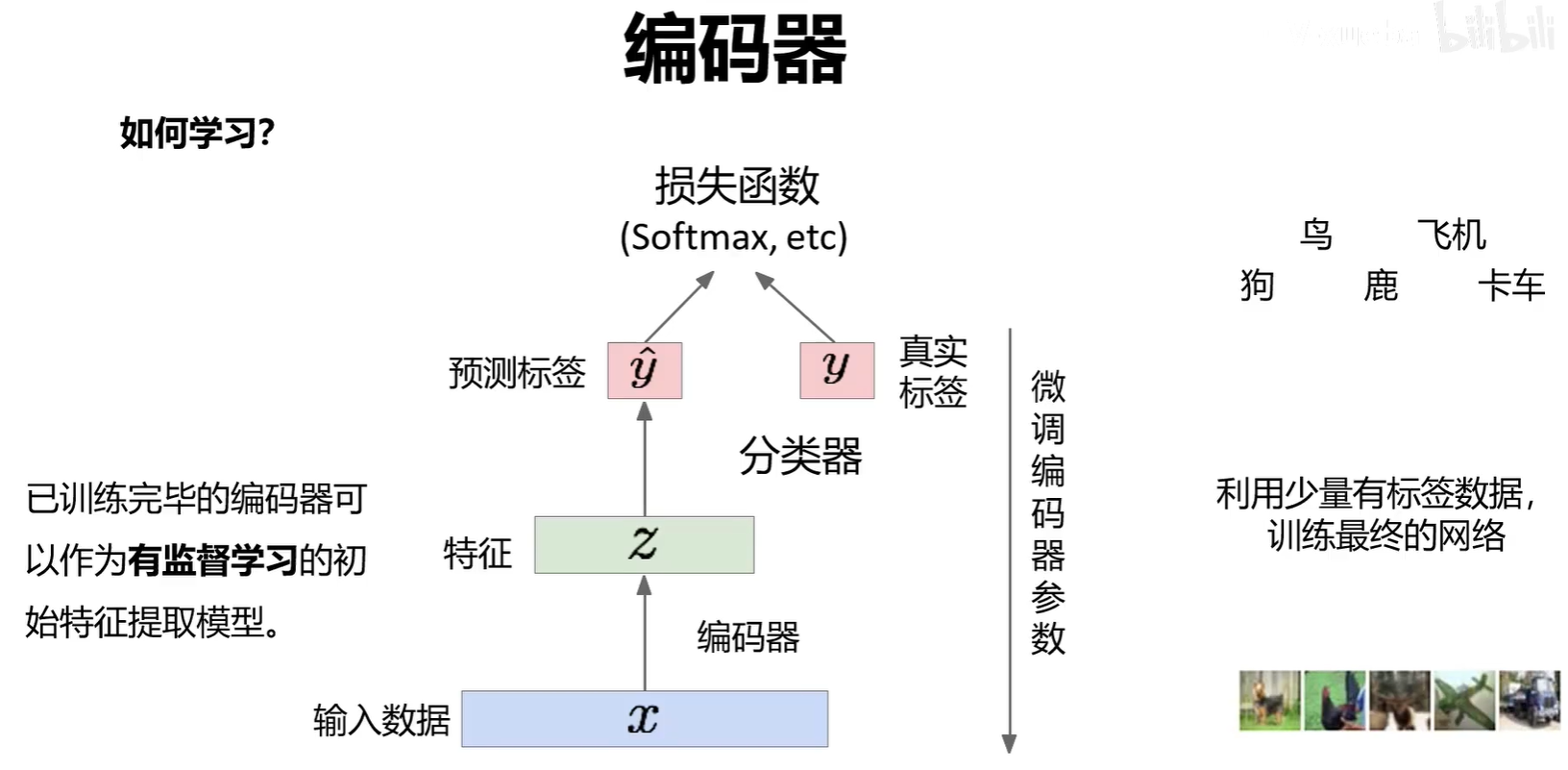
编码器可以单独作为一个特征提取网络来进行分类任务。
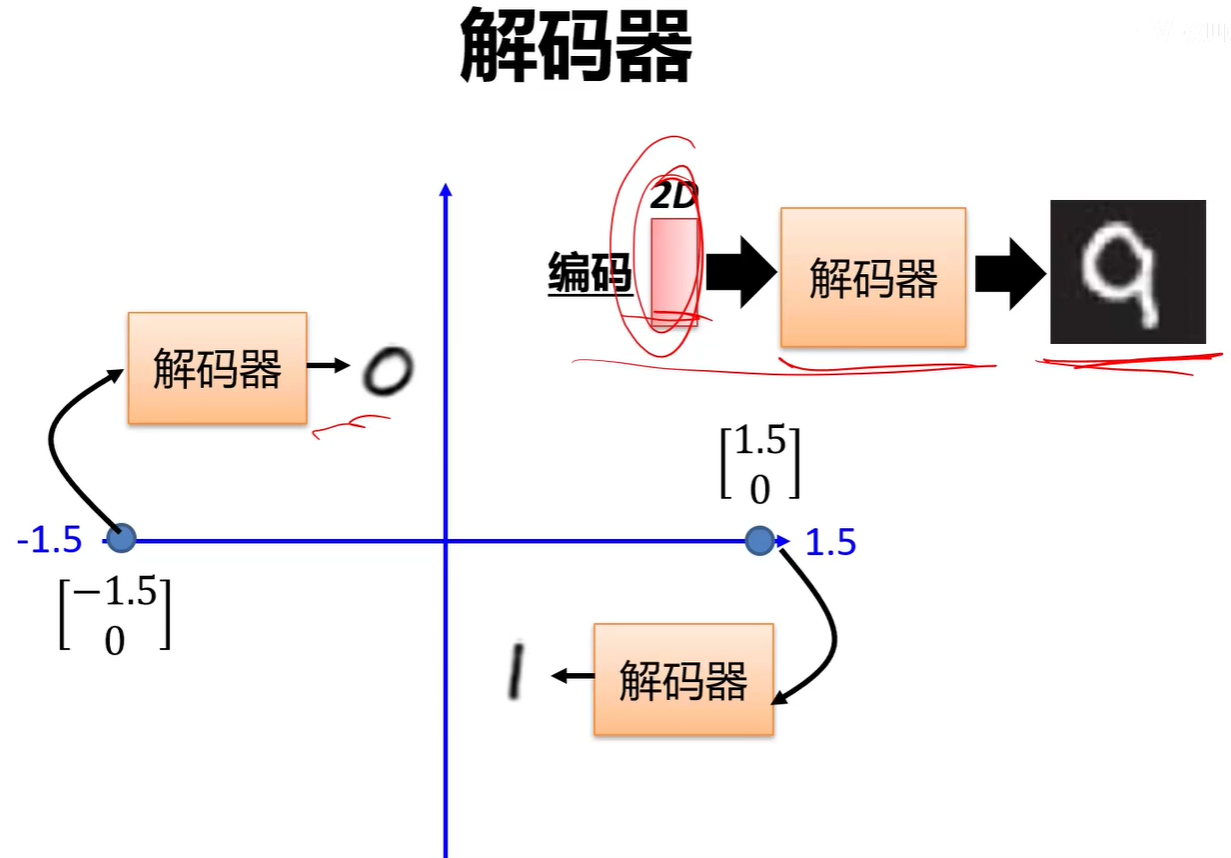
解码器可以单独分割出来作为一个图像生成器。