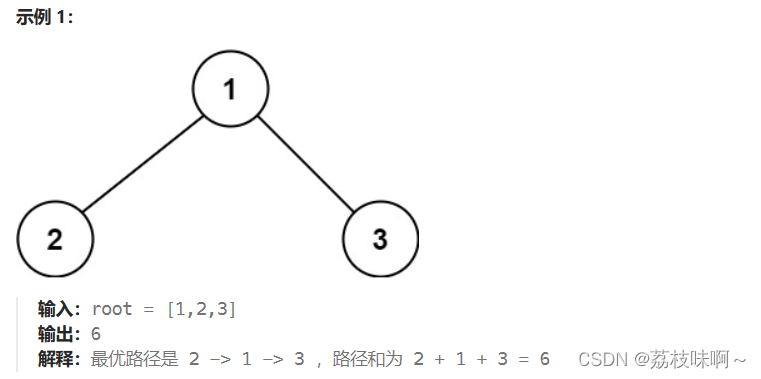
第一次只花了20分钟左右就完全靠自己把一道hard题做出来了。我这个方法还是非常简单非常容易理解的,虽然时间复杂度达到了O(n2)。以下是我的代码:
class Solution {int max;public int maxPathSum(TreeNode root) {max = Integer.MIN_VALUE;return dfs2(root);}public int dfs2(TreeNode root){if(root == null)return Integer.MIN_VALUE;max = Math.max(dfs(root), dfs(root.left)+dfs(root.right)+root.val);return Math.max(max, Math.max(dfs2(root.left), dfs2(root.right)));}public int dfs(TreeNode root){if(root == null){return 0;}return root.val + Math.max(0,Math.max(dfs(root.left), dfs(root.right)));}
}我用了两个深度优先遍历,首先第一个dfs(TreeNode root)方法是找出以root的为根节点的单向最大和的路径。
这个非常好求,root为根的单向最大和路径就是(左子树为根的单向最大路径和右子树为根的单向最大路径中的最大的+root.val),当然如果两个子节点的最大和路径都是负数,那么root它自己单独就是最大的。
第二个深度优先遍历dfs2(TreeNode root)方法是遍历整颗树的节点,找出分别以每个节点的最大和路径(不只是单向的,还可以通过根节点把左右两边连起来)的最大值,返回最大值即可。
这个也非常好求,要么是以root为根的单向的最大值dfs(root),要么是把根节点和左边最大的和右边最大的连起来dfs(root.left)+dfs(root.right)+root.val。为什么不考虑只连左边或者只连右边呢?因为第一种情况dfs(root)就是考虑了只连左或者只连右后者单独一个节点。然后进行递归找出最大值即可return Math.max(max, Math.max(dfs2(root.left), dfs2(root.right)))。
看看官方题解做法吧
看完题解我觉得我像个傻逼,一次深度遍历dfs就好了,只需要设置一个全局变量max,然后每遍历到一个节点就更新一下max就好了,所以把我的代码稍微改一下就是题解代码:
class Solution {int max;public int maxPathSum(TreeNode root) {max = Integer.MIN_VALUE;dfs(root);return max;}public int dfs(TreeNode root){if(root == null){return 0;}int lefeCon = Math.max(0,dfs(root.left));int rightCon = Math.max(0, dfs(root.right));max = Math.max(max, root.val+lefeCon+rightCon);return root.val + Math.max(0,Math.max(lefeCon, rightCon));}
}我这个dfs(TreeNode root)还是返回根节点连上左边或者连上右边的最大值(不是同时连左边和右边),然后用max是左右都连起来,max不停更新,最后返回max即可。



![[⑦ADRV902x]: JESD204学习笔记](https://img-blog.csdnimg.cn/direct/f41b8b635c144db9a1ae852ccc78b88b.png)