引言

对于快排和归并排序这个相信大家都知道，是非常重要的，不论是在找工作、考研、竞赛，这两个排序可以说是非常的重要，在面试中，面试官非常有可能就是让你手撕快排或者是归排，然后竞赛也有很多关于快排和归排的应用，等下会列出来一些具体的问题，然后接下来就开始吧。其实关于这个东西，我还是想说，其实这些背背看看就行了，但是真正有价值的是得多练多思考，多动。

一、快速排序

这个快排的思想说一下：就是每次找一个数排序，使得这个数的左边全部都小于该数，这个数的右边全都大于该数，然后再递归左半边，递归右半边。

1.模板一

这个有个注意的问题，就是这个模板的边界条件，x不能取q[r]，否则会有边界问题出现

void quick_sort(int q[], int l, int r)
{if(l >= r) return;int i = l - 1, j = r + 1, x = q[l + r >> 1];  //q[l] 或任意 但不能是q[r]while(i < j){do i++; while(q[i] < x);do j--; while(q[j] > x);if(i < j) swap(q[i], q[j]);}quick_sort(q,l,j), quick_sort(q,j+1,r);
}

2.模板二

这个模板是先把x取出来，然后从j开始遍历，j不满足就把j的值给i，然后i继续遍历，i不满足就把i的值给j，最后把x的值给i或者j

void quick_sort(int q[], int l, int r)
{if (l >= r) return;int i = l, j = r, tmp = q[l];while (i < j){while (i < j && q[j] > tmp) j--;if (i < j) q[i] = q[j];while (i < j && q[i] <= tmp) i++;if (i < j) q[j] = q[i];}q[i] = tmp;quick_sort(q, l, i), quick_sort(q, i + 1, r);
}

二、归并排序

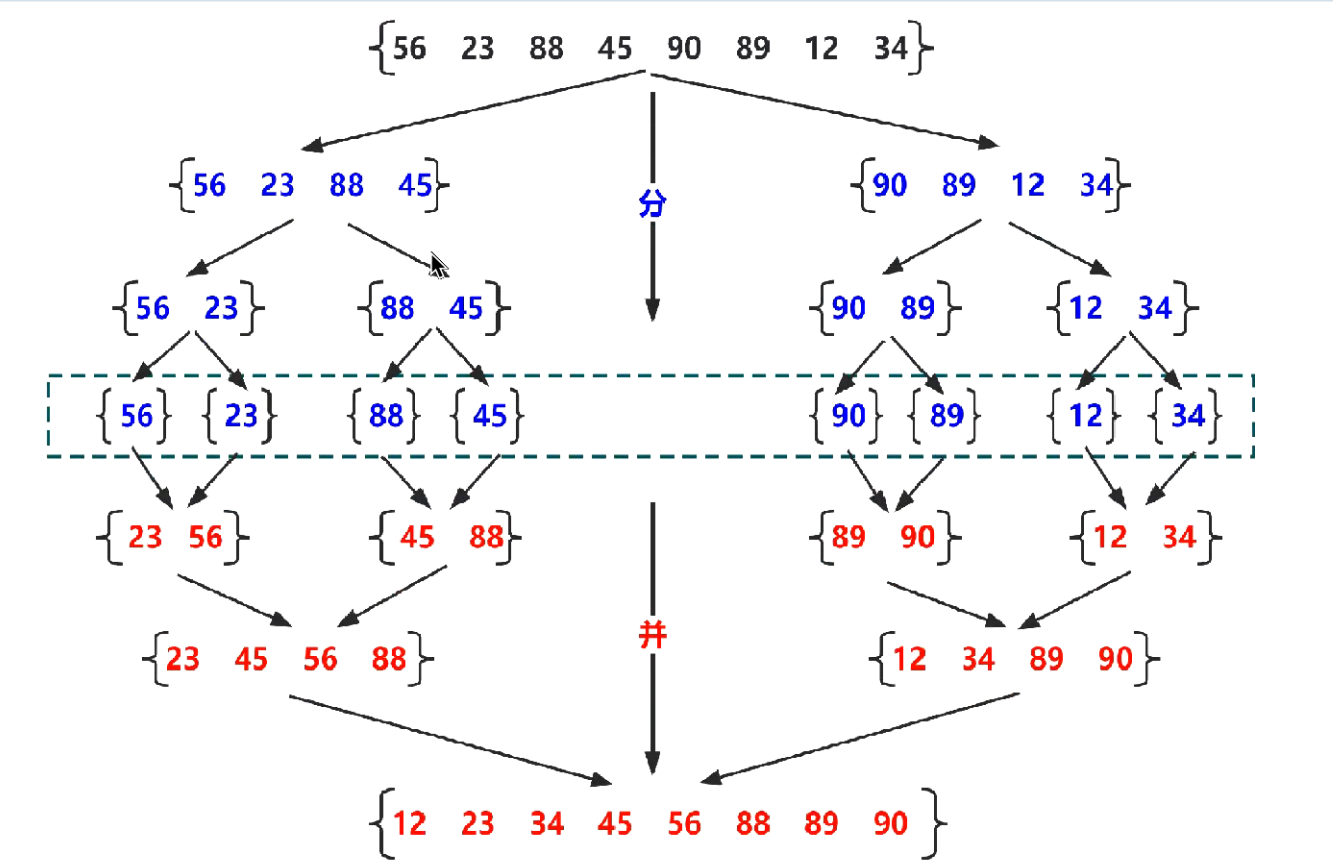
这个归并排序跟快排不同的是，快排是先排好后再分治，而归并排序是，先分治，然后到达分界条件后再递推上去排序，大概下图中的这么个方式

1.模板一

很惭愧，这个只有一个模板，因为这个不是很难，边界问题也没有，所以只有一个标准版的模板

void merge_sort(int a[], int l, int r)
{if(l >= r) return;int mid = l + r >> 1;merge_sort(a, l, mid), merge_sort(a, mid + 1, r);int i = l, j = mid + 1, k = 0;while(i <= mid && j <= r){if(a[i] < a[j]) tmp[k++] = a[i++];else tmp[k++] = a[j++];}while(i <= mid) tmp[k++] = a[i++];while(j <= r) tmp[k++] = a[j++];for(int i = l, j = 0; j < k; ++i, ++j) a[i] = tmp[j];
}

三、例题扩展

1.第k个数

给定一个长度为 n 的整数数列，以及一个整数 k，请用快速选择算法求出数列从小到大排序后的第 k 个数。输入格式
第一行包含两个整数 n 和 k。第二行包含 n 个整数（所有整数均在 1∼109 范围内），表示整数数列。输出格式
输出一个整数，表示数列的第 k 小数。数据范围
1≤n≤100000,1≤k≤n输入样例：
5 3
2 4 1 5 3
输出样例：
3

#include <cstdio>
#include <iostream>using namespace std;const int N = 1e6+10;int a[N];
int n, k;int quick_sort(int q[], int l, int r, int k)
{if(l >= r) return q[l];int i = l - 1, j = r + 1, x = q[l + r >> 1];  //q[l] 或任意 但不能是q[r]while(i < j){do i++; while(q[i] < x);do j--; while(q[j] > x);if(i < j) swap(q[i], q[j]);}if(j - l + 1 >= k) return quick_sort(q, l, j, k);else return quick_sort(q, j + 1, r, k - (j - l + 1));
}int main()
{cin >> n >> k;for(int i = 0; i < n; ++i) scanf("%d",&a[i]);cout << quick_sort(a, 0, n-1,k);return 0;
}

2.逆序对的个数

给定一个长度为 n的整数数列，请你计算数列中的逆序对的数量。逆序对的定义如下：对于数列的第 i个和第 j个元素，如果满足 i<j且 a[i]>a[j]，则其为一个逆序对；否则不是。输入格式
第一行包含整数 n，表示数列的长度。第二行包含 n个整数，表示整个数列。输出格式
输出一个整数，表示逆序对的个数。数据范围
1≤n≤100000，数列中的元素的取值范围 [1,109]。输入样例：
6
2 3 4 5 6 1
输出样例：
5

#include <cstdio>
#include <iostream>using namespace std;typedef long long LL;const int N = 1e5+10;int a[N], tmp[N];
int n;LL merge_sort(int a[], int l, int r)
{if(l >= r) return 0;int mid = l + r >> 1;LL res = 0;res += merge_sort(a, l, mid) + merge_sort(a, mid + 1, r);int i = l, j = mid + 1, k = 0;while(i <= mid && j <= r){if(a[i] <= a[j]) tmp[k++] = a[i++];else {tmp[k++] = a[j++];res += mid - i + 1;}}while(i <= mid) tmp[k++] = a[i++];while(j <= r) tmp[k++] = a[j++];for(int i = l, j = 0; i <= r; ++i, ++j) a[i] = tmp[j];return res;
}int main()
{scanf("%d", &n);for(int i = 0; i < n; ++i) scanf("%d", &a[i]);cout << merge_sort(a, 0, n-1) << endl;return 0;
}