欧拉回路欧拉路【详解】-编程知识

1.引入

2.概念

3.解决方法

4.例题

5.回顾

1.引入

经典的七桥问题

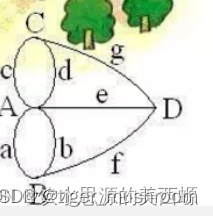
哥尼斯堡是位于普累格河上的一座城市，它包含两个岛屿及连接它们的七座桥，如下图所示。

可否走过这样的七座桥，而且每桥只走过一次？

你怎样证明？

后来大数学家欧拉把它转化成一个几何问题——一笔画问题。

我们的大数学家欧拉，找到了它的重要条件

1.奇点的数目不是0个就是2个

奇点：就是度为奇数（有向图是判断出度与入度是否相等），反之为偶点

有向图1、连通 2、所有点出度等于入度或者一个点入度-出度=1，另外一个点出度-入度=1

2.图是联通的

2.概念

欧拉路：对于一个图，每条边可以且只能访问一次

欧拉回路：在欧拉图的情况下，最后要回到原点。也就是说欧拉路不一定是欧拉回路，但欧拉回路一定是欧拉路

3.解决方法：
1.dfs

第一步：判断图是否连通

第二步：判断奇点个数

很简单，但是使用dfs的话，就需要很多数组，并且用邻接矩阵是最方便的，所以费空间

2.并查集

分为G1和G2两个集合，G1表示已经联通的，G2表示未联通的

利用父亲表示法合并集合效率最高，也是上面那两步

4.例题

（1）

一笔画问题

题目描述

如果一个无向图存在一笔画，则一笔画的路径叫做欧拉路，如果最后又回到起点，那这个路径叫做欧拉回路。

输入

第一行n，m，0 < n <=20，表示有n个点，m条边，以下m行描述每条边连接的两点。

输出

如果有欧拉路或欧拉回路，输出一条路径即可，顶点之间由空格隔开。

如果没有，输出NO

样例输入1

5 5
1 2
2 3
3 4
4 5
5 1

样例输出1

1 5 4 3 2 1

解法

1.dfs

简单，实用

费空间费时间

2.并查集

效率高，快速，不费时间不费空间

难，费劲

本蒟蒻用的是DFS

1、判断连通性，没有判断
就是要判断所有点都是连通的（dfs或者并查集）
如果不连通输出NO

2、如果连通，统计奇点的个数
如果奇点个数为0则为欧拉回路
如果奇点个数为2则为欧拉路
其他情况则输出NO

3、输出一个路径

dfs:

void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}

调题过程很坎坷

40分：（未判断NO)

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,p;
int dfs(int i)
{int j;for(j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++p]=i;return 0;
}int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;}}dfs(z);for(int i=1;i<=p;i++){cout<<c[i]<<" ";}return 0;
}//40分

60分：（未判断连通性）

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}}dfs(z);if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}//60分

100分AC：

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point,lt;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}if(d[i]==0){lt++;}}dfs(z);if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}if(lt!=0){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}//AC

5.回顾

因为我的测试点没有测出来问题所在：

问题：

如果1-2-3-4四个点一个环，5-6两个点连通，奇点个数为2，但整个图不连通

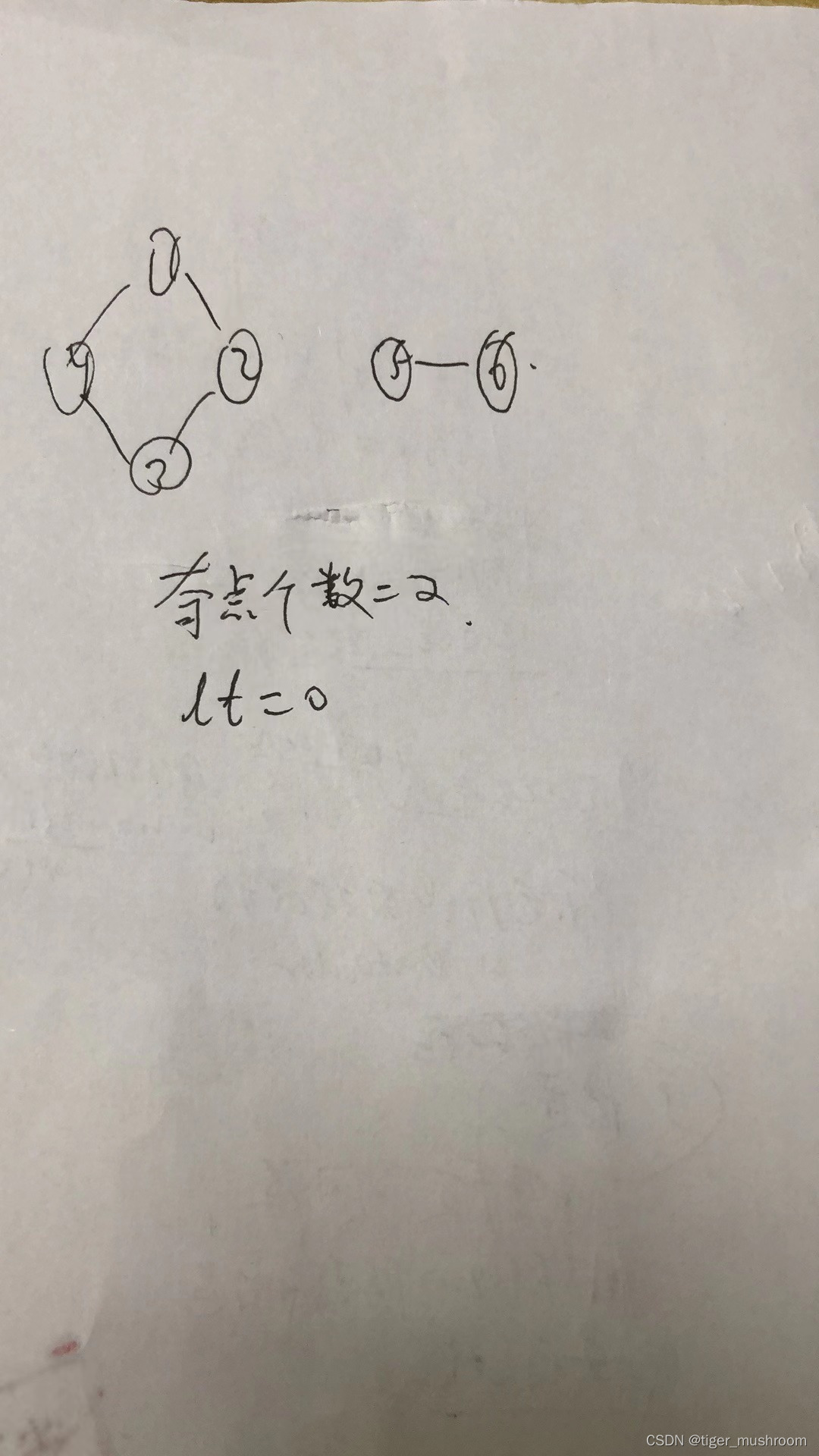
我的程序会说YES

可是根本不连通

输出5 6

碰上这样的就必须用DFS，并查集了

本蒟蒻偷了个小懒

因为碰上这样的（错误）输出一定不会是m+1个

所以判断一下输出个数是不是不等于m+1

如果不等于，输出NO。

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point,lt;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}
int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}if(d[i]==0){lt++;}}dfs(z);if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}if(lt!=0){cout<<"NO";return 0;}if(reckon!=m+1){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}

最终，我们把无用的代码段删掉，调试结束

#include<bits/stdc++.h>
using namespace std;
#define N 510
int g[N][N],d[N],c[N],n,m,reckon,oddity_point,lt;
void dfs(int i)
{for(int j=1;j<=n;j++){if(g[i][j]==1){g[i][j]=0;g[j][i]=0;dfs(j);}}c[++reckon]=i;return;
}
int main()
{cin>>n>>m;int x,y;memset(g,0,sizeof(g));for(int i=1;i<=m;i++){cin>>x>>y;g[x][y]=1;g[y][x]=1;d[x]++;d[y]++;}int z=1;for(int i=1;i<=n;i++){if(d[i]%2==1){z=i;oddity_point++;}}dfs(z);//判断连通性if(reckon!=m+1){cout<<"NO";return 0;}//判断奇点个数if(oddity_point!=2&&oddity_point!=0){cout<<"NO";return 0;}for(int i=1;i<=reckon;i++){cout<<c[i]<<" ";}return 0;
}