王道数据结构课后代码题 p149 第3—— 7（c语言代码实现）

目录

3.编写后序遍历二叉树的非递归算法

 4.试给出二叉树的自下而上、自右到左的层次遍历算法 （有图解代码详解）c语言代码实现

5.假设二叉树采用二叉链表存储结构，设计一个非递归算法求二叉树的高度。

​编辑

 6.设一棵二叉树中各结点的值互不相同，其先序遍历序列和中序遍历序列分别存于两个一维数组A[l...n]和 B[l...n]中，试编写算法建立该二叉树的二叉链表。

 7.二叉树按二叉链表形式存储，写一个判别给定二叉树是否是完全二叉树的算法

3.编写后序遍历二叉树的非递归算法

 本题代码如下

void postorder(tree* t)
{struct treenode* stack[100];//初始化结构体数组int top = -1;//让栈顶指向-1treenode* p = *t;while (p || top != -1)//p不为空，并且栈不为空{if (p){top++;//p不为空，将p压入栈中stack[top] = p;p = p->lchild;//一直向左下遍历}else{p = stack[top];//p等于栈顶元素if (p->rchild && p->rchild->tag == 0)//右孩子不为空且未被访问过p = p->rchild;else//否则弹出结点并访问{p = stack[top];top--;printf("%c", p->data);p->tag = 1;//标记p被访问过p = NULL;}}}
}

完整测试代码

#include<stdio.h>
#include<stdlib.h>
typedef struct treenode
{char data;struct treenode* lchild, * rchild;int tag;
}treenode,*tree;
void buildtree(tree *t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->tag = 0;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
void postorder(tree* t)
{struct treenode* stack[100];//初始化结构体数组int top = -1;//让栈顶指向-1treenode* p = *t;while (p || top != -1)//p不为空，并且栈不为空{if (p){top++;//p不为空，将p压入栈中stack[top] = p;p = p->lchild;//一直向左下遍历}else{p = stack[top];//p等于栈顶元素if (p->rchild && p->rchild->tag == 0)//右孩子不为空且未被访问过p = p->rchild;else//否则弹出结点并访问{p = stack[top];top--;printf("%c", p->data);p->tag = 1;//标记p被访问过p = NULL;}}}
}
int main()
{tree t;buildtree(&t);postorder(&t);return 0;
}

用ABD##E##CF##G##

/*        A
    B        C
D      E   F     G    
*/

 4.试给出二叉树的自下而上、自右到左的层次遍历算法 （有图解代码详解）c语言代码实现

 本题我们采用让结点出队时将结点入栈，同时访问该结点，是否有左右孩子，如果有的话，就让左右孩子进队。最后所有结点都入栈了，再从栈顶开始依次访问就可以得到结果

看下面的图解

A先入队，然后出队，就压入栈中

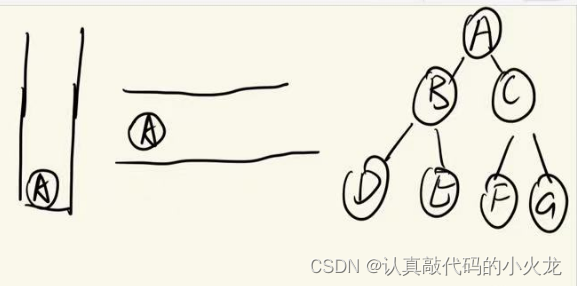
访问A结点，有左右孩子，左右孩子入队

B结点出队并入栈，并访问B结点，B结点有左右孩子，左右孩子进队

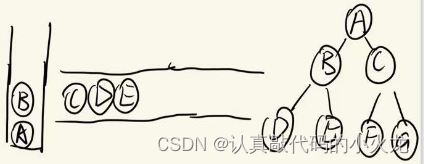
C结点出队并入栈，同时访问C结点，C结点有左右孩子，左右孩子进队

D结点出队并入栈，同时访问D结点，D结点没有左右孩子

EFG依次出队进栈（与D的步骤相同）

最后我们看一下栈中的元素

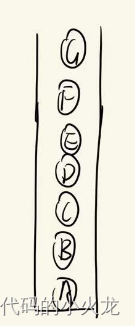
我们让栈中元素依次出栈就能得到我们想要的结果

下面我们来看一下代码该如何实现：

void level(tree* t)
{treenode* q[10];treenode* s[10];int top = -1;int f = -1;int r = -1;treenode* p;q[++r] = *t;//根结点进队while (f < r){p = q[++f];//结点出队s[++top] = p;//结点进栈if (p->lchild)//出队结点是否有左孩子q[++r] = p->lchild;//有左孩子，左孩子进栈if (p->rchild)//出队结点是否有右孩子q[++r] = p->rchild;//有右孩子，右孩子进栈}while (top != -1)//依次输出栈中元素{printf("%c ", s[top--]->data);}
}

完整测试代码如下

#include<stdio.h>
#include<stdlib.h>
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
}treenode,*tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
void level(tree* t)
{treenode* q[10];treenode* s[10];int top = -1;int f = -1;int r = -1;treenode* p;q[++r] = *t;while (f < r){p = q[++f];s[++top] = p;if (p->lchild)q[++r] = p->lchild;if (p->rchild)q[++r] = p->rchild;}while (top != -1){printf("%c ", s[top--]->data);}
}
int main()
{tree t;buildtree(&t);level(&t);return 0;
}

用ABD##E##CF##G##测试

5.假设二叉树采用二叉链表存储结构，设计一个非递归算法求二叉树的高度。

 采用层次遍历的算法，设置变量 ans记录当前结点所在的层数，设置变量 l 指向当前层的最右结点，每次层次遍历出队时与 l指针比较，若两者相等，则层数加 1，并让 l指向下一层的最右结点，直到遍历完成。ans的值即为二又树的高度。

本题代码如下

int deep(tree* t)//求树的深度
{if ((*t) == NULL)return 0; treenode* q[10];int f = -1, r = -1;//f头结点，r尾结点int l = 0, ans = 0;//l每次指向每层的最后一个结点q[++r] = *t;treenode* p;while (f < r){p = q[++f];//队列元素出队，正在访问的结点if (p->lchild)q[++r] = p->lchild;//左孩子入队if (p->rchild)q[++r] = p->rchild;//右孩子入队if (f == l)//处理该层的最右结点{ans++;//层数+1l = r;//让l指向下一层}}return ans;
}

完整测试代码

#include<stdio.h>  
#include<stdlib.h>  
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
}treenode, * tree;
void buildtree(tree* t)//建树
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
int deep(tree* t)//求树的深度
{if ((*t) == NULL)return 0; treenode* q[10];int f = -1, r = -1;//f头结点，r尾结点int l = 0, ans = 0;//l每次指向每层的最后一个结点q[++r] = *t;treenode* p;while (f < r){p = q[++f];//队列元素出队，正在访问的结点if (p->lchild)q[++r] = p->lchild;//左孩子入队if (p->rchild)q[++r] = p->rchild;//右孩子入队if (f == l)//处理该层的最右结点{ans++;//层数+1l = r;//让l指向下一层}}return ans;
}
int main()
{tree t;buildtree(&t);printf("树的高度为：%d\n", deep(&t)); return 0;
}
/*			AB        CD     E  F    */
//ABD##E##CF###

 6.设一棵二叉树中各结点的值互不相同，其先序遍历序列和中序遍历序列分别存于两个一维数组A[l...n]和 B[l...n]中，试编写算法建立该二叉树的二叉链表。

 本题代码如下

tree build(char a[], char b[], int s, int e)
{if (s <= e){treenode* root = (treenode*)malloc(sizeof(treenode));root->data = a[pos];//将子树的根节点赋值给rootint i;for (i = s; i <= e; i++)//在b数组中找到根节点if (b[i] == root->data)break;pos++;root->lchild = build(a, b, s, i - 1);//建立左子树root->rchild = build(a, b, i + 1, e);//建立右子树return root;}return NULL;
}

完整测试代码

#include<stdio.h>
typedef struct treenode {char data;struct treenode* lchild, * rchild;
}treenode,*tree;
int pos = 0;//全局变量pos
tree build(char a[], char b[], int s, int e)
{if (s <= e){treenode* root = (treenode*)malloc(sizeof(treenode));root->data = a[pos];//将子树的根节点赋值给rootint i;for (i = s; i <= e; i++)//在b数组中找到根节点if (b[i] == root->data)break;pos++;root->lchild = build(a, b, s, i - 1);//建立左子树root->rchild = build(a, b, i + 1, e);//建立右子树return root;}return NULL;
}
void disp(tree t)
{if (t){disp(t->lchild);disp(t->rchild);printf("%c", t->data);}
}
int main(){char a[] = {'A','B','D','E','C','F'};//先序char b[] = {'D','B','E','A','F','C' };//中序tree root = build(a, b, 0, 5);printf("后序序列为:");disp(root);return 0;
}

 7.二叉树按二叉链表形式存储，写一个判别给定二叉树是否是完全二叉树的算法

 采用层次遍历算法，将所有结点加入队列(包括空结点)。

如果没有左孩子，就看有没有右孩子，如果有右孩子，那么不为完全二叉树。

如果有左孩子，且之前不存在缺孩子的结点，左孩子进队，如果有右孩子，右孩子也进队，否则就是缺孩子了。之前存在缺孩子的，那么就不是完全二叉树。

有两种代码的写法

本题代码如下

int isok(tree* t)//判断完全二叉树
{squene q;q.f = q.r = q.tag = 0;int flag = false; // 标志是否遇到了空节点if (*t == NULL)return true; // 空树也是完全二叉树enquene(&q, *t);treenode* p;while (!isempty(&q)){dequene(&q, &p);if (p->lchild){if (flag) // 如果之前遇到了空节点，说明不是完全二叉树return false;enquene(&q, p->lchild);}else{flag = true;}if (p->rchild){if (flag) // 如果之前遇到了空节点，说明不是完全二叉树return false;enquene(&q, p->rchild);}else{flag = true;}}return true;
}

完整测试代码

#include <stdio.h>
#include <stdlib.h>
#define Max 15
#define true 1
#define false 0
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
} treenode, * tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}
typedef struct squene
{struct treenode* data[Max];int f, r, tag;
} squene;
int isempty(squene* q)//判断队空
{if (q->f == q->r && q->tag == 0)return true;return false;
}
int isfull(squene* q)//判断队满
{if (q->f == q->r && q->tag == 1)return true;return false;
}
int enquene(squene* q, treenode* p)//进队操作
{if (isfull(q))return false;q->data[q->r] = p;q->r = (q->r + 1) % Max;q->tag = 1;return true;
}
int dequene(squene* q, treenode** p)//出队操作
{if (isempty(q))return false;*p = q->data[q->f];q->f = (q->f + 1) % Max;q->tag = 0;return true;
}
int isok(tree* t)//判断完全二叉树
{squene q;q.f = q.r = q.tag = 0;int flag = false; // 标志是否遇到了空节点if (*t == NULL)return true; // 空树也是完全二叉树enquene(&q, *t);treenode* p;while (!isempty(&q)){dequene(&q, &p);if (p->lchild){if (flag) // 如果之前遇到了空节点，说明不是完全二叉树return false;enquene(&q, p->lchild);}else{flag = true;}if (p->rchild){if (flag) // 如果之前遇到了空节点，说明不是完全二叉树return false;enquene(&q, p->rchild);}else{flag = true;}}return true;
}
int main()
{treenode* t;buildtree(&t);if (isok(&t))printf("yes");elseprintf("no");return 0;
}

用ABD##E##CF##G##测试

/*                A

        B                C

D        E        F        G      

*/

用ABD###CF##G##测试

/*                A

        B                C

D                  F        G

*/

还可以用另外一种写法

#include <stdio.h>
#include <stdlib.h>
#define Max 15
typedef struct treenode
{char data;struct treenode* lchild, * rchild;
} treenode, * tree;
void buildtree(tree* t)
{char ch;ch = getchar();if (ch == '#')*t = NULL;else{*t = (treenode*)malloc(sizeof(treenode));(*t)->data = ch;(*t)->lchild = NULL;(*t)->rchild = NULL;buildtree(&(*t)->lchild);buildtree(&(*t)->rchild);}
}int isok(tree* t)//判断完全二叉树
{treenode* q[Max];int f = -1, r = -1;int tag = 1;//标记是否为完全二叉树q[++r] = *t;treenode* p;int flag = 1;//标记缺孩子if (*t == NULL) {tag = 1;}if (!(*t)->lchild && !(*t)->rchild)tag = 1;while (f < r) {p = q[++f];if (!p->lchild) //没有左孩子缺孩子{flag = 0;if (p->rchild)tag = 0;}else//有左孩子{if (flag)//之前不存在缺孩子的结点{q[++r] = p->lchild;if (p->rchild)q[++r] = p->rchild;elseflag = 0;}else//之前存在缺孩子的结点tag = 0;}}if (tag)return 1;return 0;
}
int main()
{treenode* t;buildtree(&t);if (isok(&t))printf("yes");elseprintf("no");return 0;
}

用ABD##E##CF##G##

/*                A

        B                C

D        E        F        G      

*/

测试结果为

用AB#E##CF###

/*                A

        B                C

            E        F   

*/

测试结果为

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/264066.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

普冉PY32系列(十三) SPI驱动WS2812全彩LED

普冉PY32系列(十三) SPI驱动WS2812全彩LED

目录 普冉PY32系列(一) PY32F0系列32位Cortex M0 MCU简介普冉PY32系列(二) Ubuntu GCC Toolchain和VSCode开发环境普冉PY32系列(三) PY32F002A资源实测 - 这个型号不简单普冉PY32系列(四) PY32F002A/003/030的时钟设置普冉PY32系列(五) 使用JLink RTT代替串口输出日志普冉PY32…
阅读更多...
STM32——继电器

STM32——继电器

继电器工作原理 单片机供电 VCC GND 接单片机&#xff0c; VCC 需要接 3.3V &#xff0c; 5V 不行&#xff01; 最大负载电路交流 250V/10A &#xff0c;直流 30V/10A 引脚 IN 接收到 低电平 时&#xff0c;开关闭合。
阅读更多...
Mac电脑投屏AirServer 2024怎么下载安装激活许可期限

Mac电脑投屏AirServer 2024怎么下载安装激活许可期限

对于那些想要将 iPhone、iPad 或其他 iOS 设备上的小屏幕镜像到计算机上的大屏幕的人来说&#xff0c;AirPlay 是一个很好的工具。 基于此&#xff0c;AirServer 非常需要将您的 Mac 或 PC 变成 AirPlay 设备。 但是如何使用计算机上的设置对 iPhone 等 iOS 设备进行屏幕镜像&a…
阅读更多...
JAVA实操经验

JAVA实操经验

零&#xff1a; 按照需要&#xff0c;可以使用需要某个类下&#xff08;主要是java提供的&#xff09;的方法来实现某个功能。&#xff08;主要是用在不同类下的方法会进行重写功能不同&#xff09; 方法和构造方法不同&#xff1a;方法是方法&#xff0c;构造方法是构造器&a…
阅读更多...
Sql server数据库数据查询

Sql server数据库数据查询

请查询学生信息表的所有记录。 答&#xff1a;查询所需的代码如下&#xff1a; USE 学生管理数据库 GO SELECT * FROM 学生信息表 执行结果如下&#xff1a; 查询学生的学号、姓名和性别。 答&#xff1a;查询所需的代码如下&#xff1a; USE 学生管理数据库 GO SELE…
阅读更多...
原来JMeter 结果处理常见问题这么简单，可惜没早点看到！

原来JMeter 结果处理常见问题这么简单，可惜没早点看到！

1. 前言 工作中用 jmeter 请求一个接口对谈得上会 jmeter 的人似乎都是可以做出来的&#xff0c;但是实际难点是参数化&#xff0c;结果的断言&#xff0c;结果的汇总等。本文将针对结果过滤有效性的情况展开分析。 示例场景&#xff1a;一个接口需要对入参1000多个数据做测试…
阅读更多...
西南科技大学C++程序设计实验十（函数模板与类模板）

西南科技大学C++程序设计实验十（函数模板与类模板）

一、实验目的 1. 掌握函数模板与类模板； 2. 掌握数组类、链表类等线性群体数据类型定义与使用； 二、实验任务 1. 分析完善以下程序，理解模板类的使用： （1）补充类模板声明语句。 （2）创建不同类型的类对象，使用时明确其数据类型？ _template<typename T>__…
阅读更多...
windows安装protoc、protoc-gen-go、protoc-gen-go-grpc

windows安装protoc、protoc-gen-go、protoc-gen-go-grpc

文章目录 一、 protoc二、protoc-gen-go三、protoc-gen-go-grpc 一、 protoc 1&#xff0c;下载&#xff1a;https://github.com/google/protobuf/releases 下载对应的protoc&#xff0c;注意选择windows 2&#xff0c;下好之后解压就行&#xff0c;然后把bin目录加入到环境…
阅读更多...
找不到WMVCORE.dll怎么办?一键解决WMVCORE.dll缺失的详细方法分享

找不到WMVCORE.dll怎么办?一键解决WMVCORE.dll缺失的详细方法分享

当打开软件时提示wmvcore.dll丢失&#xff0c;这可能是由于以下几个原因导致的&#xff1a; 系统文件损坏&#xff1a;wmvcore.dll是系统文件&#xff0c;可能会因为各种原因&#xff08;如病毒感染、系统错误、软件卸载等&#xff09;而损坏。 软件依赖问题&#xff1a;某些…
阅读更多...
全面解析“由于找不到hid.dll,无法继续执行代码”的4个解决方法

全面解析“由于找不到hid.dll,无法继续执行代码”的4个解决方法

在计算机使用过程中&#xff0c;我们经常会遇到一些错误提示&#xff0c;其中之一就是“找不到hid.dll”。这个问题通常出现在尝试运行某个程序或访问某个设备时。那么&#xff0c;当我们遇到这个问题时&#xff0c;应该如何解决呢&#xff1f;本文将详细介绍找不到hid.dll的解…
阅读更多...
2023-12-10 LeetCode每日一题（爬楼梯）

2023-12-10 LeetCode每日一题（爬楼梯）

2023-12-10每日一题 一、题目编号 70. 爬楼梯二、题目链接 点击跳转到题目位置 三、题目描述 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。 每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢&#xff1f; 示例 1&#xff1a; 示例 2&#xff1a; 提…
阅读更多...
[CTFshow 红包挑战] 刷题记录

[CTFshow 红包挑战] 刷题记录

文章目录 红包挑战7红包挑战8红包挑战9 红包挑战7 考点&#xff1a;xdebug拓展 源码 <?php highlight_file(__FILE__); error_reporting(2);extract($_GET); ini_set($name,$value);system("ls ".filter($_GET[1])."" );function filter($cmd){$cmd s…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023