更多资料获取
📚 个人网站:ipengtao.com
Sympy是Python中一个强大的符号计算库,为数学和科学计算提供了丰富的功能。本文将深入介绍Sympy库的各项功能,并提供丰富的示例代码,以帮助大家更好地理解和应用这一工具。
Sympy基础
符号与表达式
Sympy的核心是符号和表达式的处理。我们将学习如何定义符号、构建表达式,并进行基本的代数运算。例如:
from sympy import symbols, expand, factorx, y = symbols('x y')
expression = (x + y)**2
expanded_expression = expand(expression)
factored_expression = factor(expression)
解方程和不等式
Sympy提供了强大的方程和不等式求解功能。通过以下代码,可以解一个方程和一个不等式:
from sympy import solve, Eqequation = Eq(x**2 - 4, 0)
solution = solve(equation, x)inequality = x**2 - 4 > 0
inequality_solution = solve(inequality, x)
微积分与极限
求导与积分
Sympy支持对表达式进行微分和积分操作。以下是一个求导和积分的示例:
from sympy import diff, integratederivative = diff(x**3, x)
integral = integrate(x**3, x)
极限
计算极限是微积分中的重要操作,Sympy可以轻松处理极限问题:
from sympy import limit, ooexpression_limit = limit(1/x, x, oo)
线性代数与矩阵
Sympy还提供了线性代数和矩阵计算的功能,包括矩阵的定义、求逆、特征值等:
from sympy import MatrixA = Matrix([[1, 2], [3, 4]])
inverse_A = A.inv()
eigenvalues_A = A.eigenvals()
微分方程
解微分方程是Sympy的强项之一,通过以下代码,可以解一个简单的微分方程:
from sympy import dsolve, Function, Eqf = Function('f')
diff_eq = Eq(f(x).diff(x, x) + f(x), 0)
solution_diff_eq = dsolve(diff_eq)
实际应用案例
通过一个更加丰富的实际案例来展示Sympy在科学计算和工程应用中的强大功能。假设要解决一个简单的电路问题,其中包含电阻、电感和电容。
from sympy import symbols, Function, Eq, dsolvet, R, L, C = symbols('t R L C')
I = Function('I')(t)# 定义电路方程
circuit_eq = Eq(L * I.diff(t, t) + R * I.diff(t) + 1/C * I, 0)# 解电路方程
solution_circuit = dsolve(circuit_eq)# 显示解
print(solution_circuit)
这段代码使用Sympy解决了包含电感、电阻和电容的电路方程。通过这个案例,读者可以清晰地看到Sympy如何在科学和工程领域中发挥作用,为复杂的数学问题提供清晰而精确的解决方案。
高级数学建模
Sympy不仅可以用于解决基础的数学问题,还可以进行高级数学建模。考虑一个机械振动的问题,可以使用Sympy来建立和求解微分方程,得到系统的振动响应。
from sympy import symbols, Function, Eq, dsolvet, m, c, k = symbols('t m c k')
x = Function('x')(t)# 定义振动方程
vibration_eq = Eq(m * x.diff(t, t) + c * x.diff(t) + k * x, 0)# 解振动方程
solution_vibration = dsolve(vibration_eq)# 显示解
print(solution_vibration)
这个例子展示了Sympy在复杂物理系统建模方面的强大功能。通过解决微分方程,可以获取系统振动的精确解。这对于工程师在设计和优化机械系统时提供了有力的工具。
性能优化与扩展
在实际的数学建模和计算过程中,性能是一个关键的考虑因素。Sympy提供了一些方法来优化计算速度,特别是在处理大规模或复杂的数学表达式时。
符号计算优化
在符号计算中,有时候可以通过对表达式进行简化或使用更有效的算法来提高性能。Sympy提供了一系列的简化函数,例如simplify、trigsimp等,可以根据表达式的特性选择合适的简化方式。
from sympy import symbols, simplify, sinx, y = symbols('x y')expr = sin(x)**2 + sin(x)**2
simplified_expr = simplify(expr)print(simplified_expr)
编译为函数
Sympy还支持将符号表达式编译为可调用的数值函数,这可以显著提高计算速度。使用lambdify函数可以将Sympy表达式转化为NumPy函数,从而利用NumPy的高性能数值计算能力。
from sympy import lambdify, symbols, sinx = symbols('x')
expr = sin(x)# 将表达式编译为函数
func = lambdify(x, expr, 'numpy')# 使用编译后的函数进行数值计算
result = func(0.5)print(result)
使用数值类型
对于一些不需要符号精度的计算,可以使用数值类型进行计算,以提高性能。
from sympy import N, sqrtexpr = sqrt(2)# 将表达式转换为浮点数
result = N(expr)print(result)
C语言扩展
Sympy还支持通过C语言扩展来加速计算。通过使用cython或SymPy Gamma,可以将一些计算转换为更高效的C语言代码。
from sympy import symbols, lambdifyx, y = symbols('x y')
expr = x**2 + y**2# 将表达式编译为C语言函数
c_func = lambdify((x, y), expr, 'C')# 使用C语言函数进行数值计算
result = c_func(2, 3)print(result)
总结
在本篇文章中,我们分享了Sympy库的高级数学建模能力以及性能优化与扩展方面的内容。通过实际案例,展示了Sympy在解决复杂的微积分问题和高级数学建模中的强大功能。Sympy的符号计算使得数学表达式的处理更为精确和灵活,为工程师和科学家提供了强大的工具。
在性能优化方面,介绍了一些实用的技巧,包括符号计算的优化、编译为函数、使用数值类型以及C语言扩展。这些方法可以显著提高Sympy在实际计算中的效率,使其更适用于处理大规模或复杂的数学问题。
Sympy不仅是一个功能强大的符号计算库,而且具有良好的可扩展性,可以通过各种优化手段满足不同场景下的需求。通过深入学习Sympy的高级功能和性能优化技巧,将能够更好地应用Sympy解决实际问题,并在数学建模和科学计算中取得更高的效率。
Python学习路线
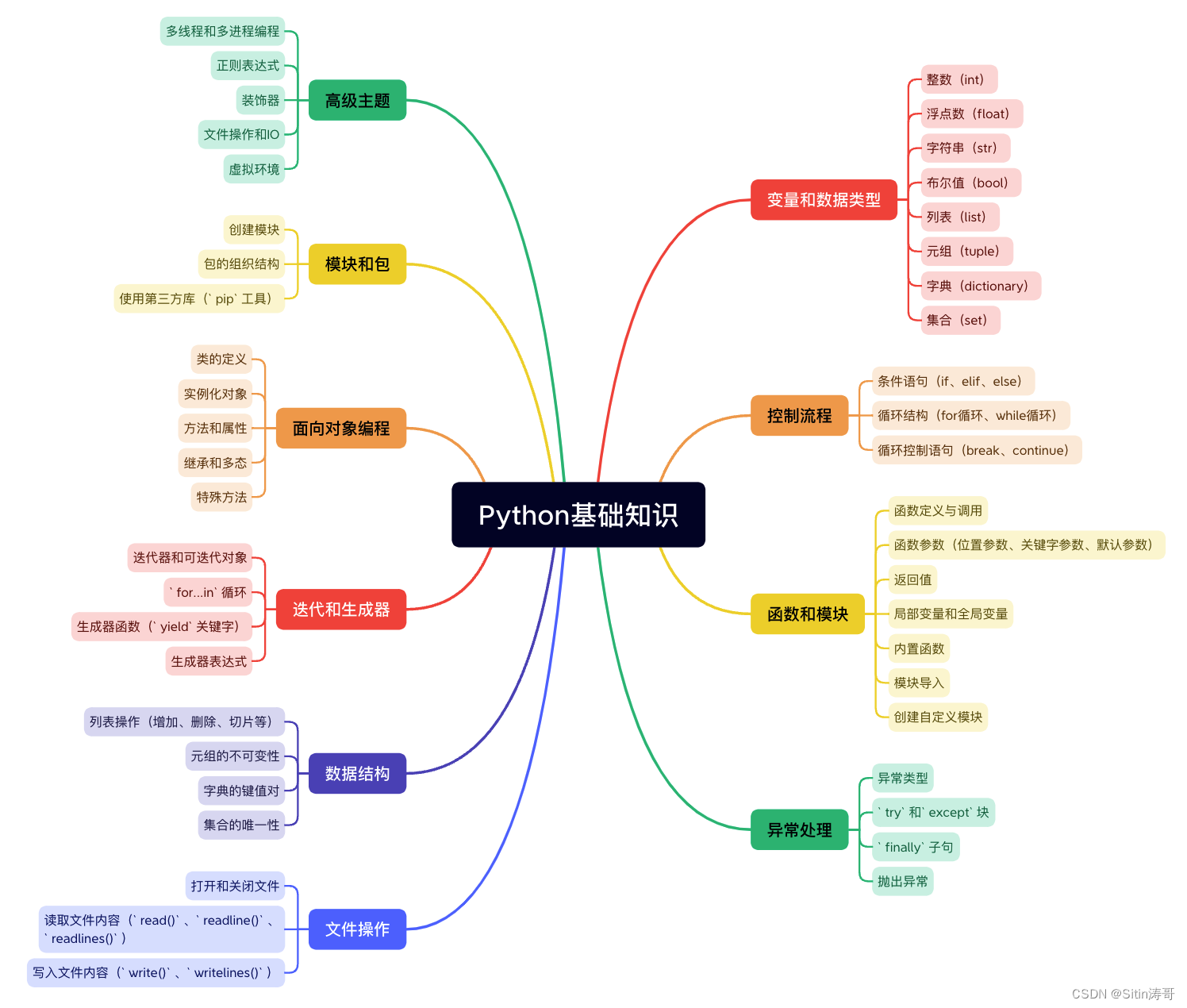
更多资料获取
📚 个人网站:ipengtao.com
如果还想要领取更多更丰富的资料,可以点击文章下方名片,回复【优质资料】,即可获取 全方位学习资料包。

点击文章下方链接卡片,回复【优质资料】,可直接领取资料大礼包。