二叉树的最大深度和二叉树的最小深度以及完全二叉树的节点个数
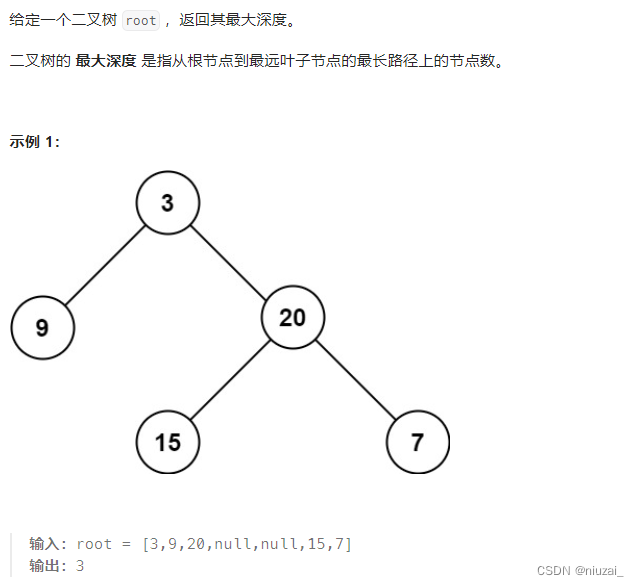
思想:可以使用迭代法或者递归!使用递归更好,帮助理解递归思路!明确递归三部曲–①确定参数以及返回参数 ②递归结束条件 ③单层逻辑是怎么样的!
class Solution:def maxDepth(self, root: Optional[TreeNode]) -> int:def dp(node):if not node:return 0left_length = dp(node.left)right_length = dp(node.right)return 1 + max(left_length, right_length)return dp(root)
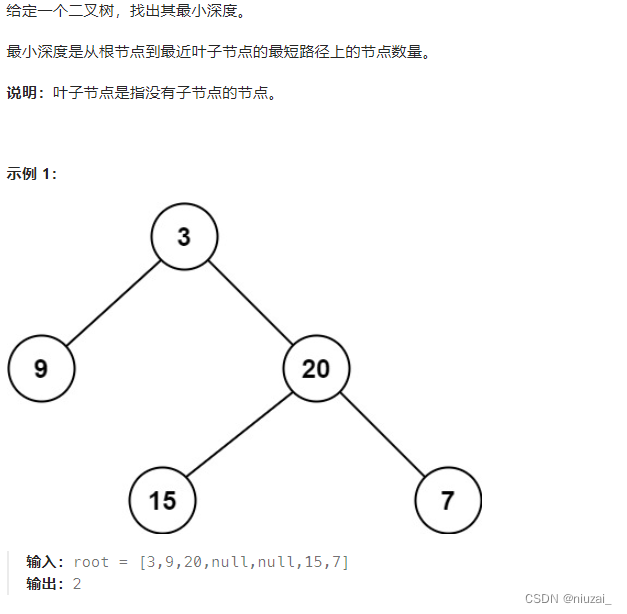
思想:看似和最大深度相似,实则不同的!还需要考虑一个节点为None但是另一个不为None的情况!这个是关键!如果是参加面试最好使用迭代法来做,也就是广度优先遍历这样会更快更好理解【判断节点是否有左右节点即可】
class Solution:def minDepth(self, root: Optional[TreeNode]) -> int:def deth_dp(node):if not node:return 0left_length = deth_dp(node.left)right_length = deth_dp(node.right)if not node.left and node.right:return 1 + right_lengthelif node.left and not node.right:return 1 + left_lengthreturn 1 + min(left_length, right_length)return deth_dp(root)
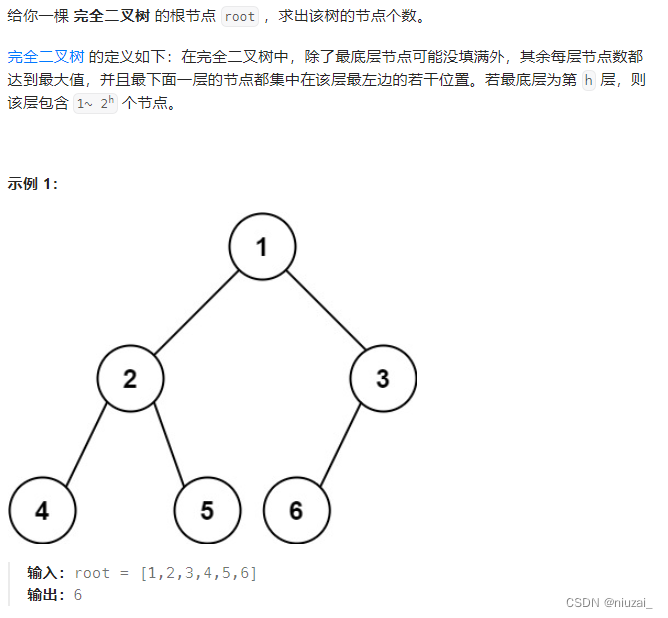
思想:和最大深度很像,返回值等于左右节点相加即可!
class Solution:def countNodes(self, root: Optional[TreeNode]) -> int:def add_deth(node):if not node:return 0left_length = add_deth(node.left)right_length = add_deth(node.right)return 1 + left_length + right_lengthreturn add_deth(root)