代码随想录二刷｜二叉树｜ 110.平衡二叉树-编程知识

代码随想录二刷｜二叉树｜ 110.平衡二叉树

题目描述
解题思路
- 递归
- 迭代
代码实现
- 递归法
- 迭代法

题目描述

110.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

示例 1：
在这里插入图片描述
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：
在这里插入图片描述
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

提示：

树中的节点数在范围 [0, 5000] 内
-104 <= Node.val <= 104

解题思路

二叉树节点的高度：从根节点到该节点的最长简单路径边的条数

二叉树节点的深度：从该节点到叶子节点的最长简单路径变的条数

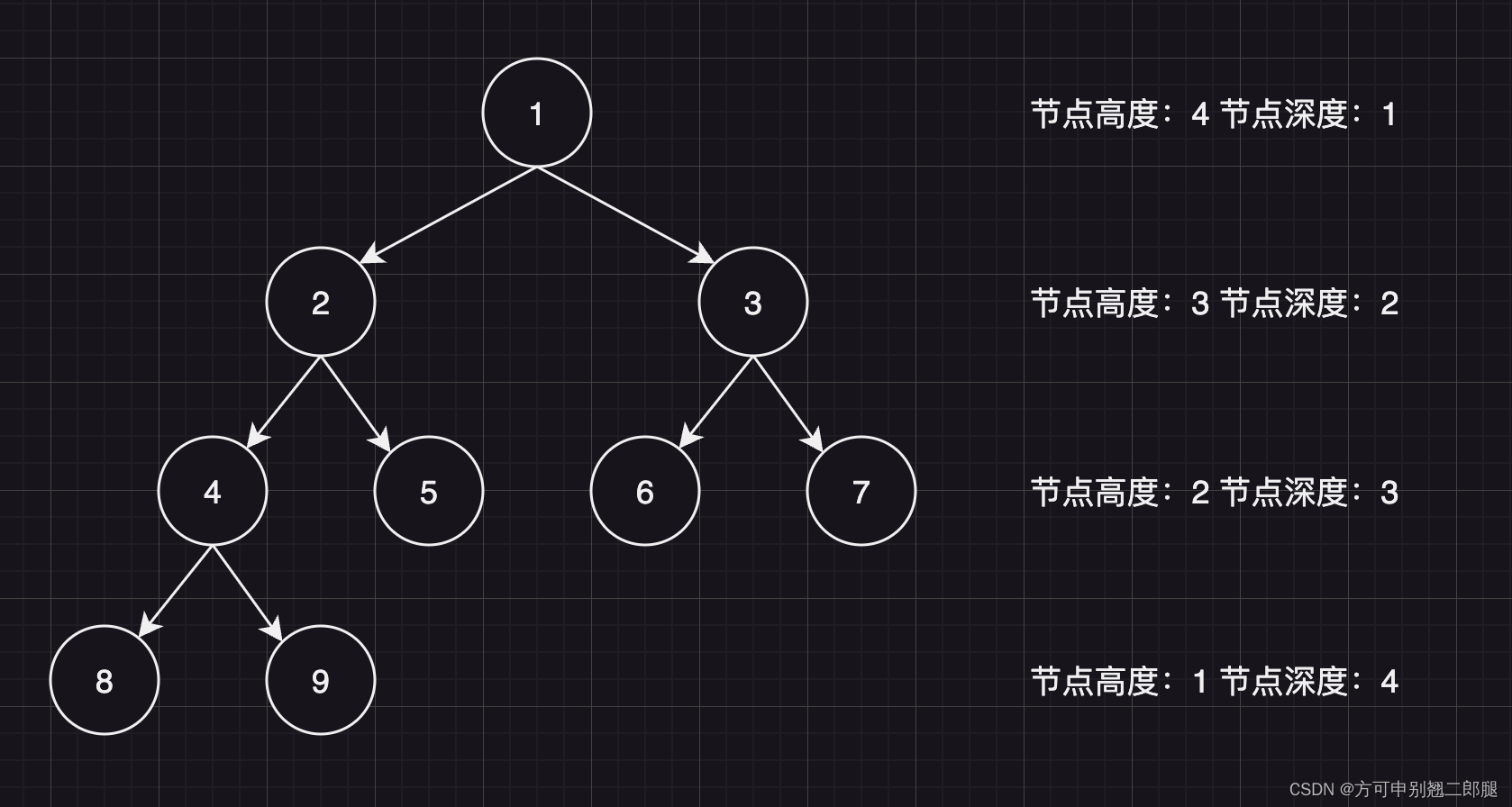
在这里插入图片描述
求深度可以从上到下去查询，所以需要前序遍历，而求高度只能从下到上去查，只能后序遍历。

因此本题使用后序遍历。

递归

递归三部曲

确定递归函数的参数和返回值
参数：当前传入的节点
返回值：因为求的是高度，所以为int

如果当前传入节点为根节点的二叉树已经不是二叉平衡树了，还返回高度的话就没有意义了。

所以如果已经不是二叉平衡树了，可以返回 -1 来标记已经不符合平衡树的规则了。
```
int getHeight(TreeNode* node)
```
确定终止条件
遇到空节点时终止，返回0，表示当前节点为根节点的树高度为 0
```
if (node == NULL) {return 0;
}
```

确定单层递归的逻辑
分别求出左右子树的高度，如果差值小于等于 1 ，则返回当前二叉树的高度，否则返回 -1，表示已经不是平衡二叉树了。

int leftHeight = getHeight(node->left);
if (leftHeight == -1) return -1;
int rightHeight = getHeight(ndoe->right);
if (rightHeight == -1) return -1;
int result;
if (abs(leftHeight - rightHeight) > 1) {result = -1;	
} else {result = 1 + max(leftHeight, rightHeight);
}
return result;

迭代

本题的迭代方式可以先定义一个函数，专门用来求高度。

这个函数通过栈模拟的后序遍历找每一个节点的高度（其实是通过求传入节点为根节点的最大深度来求的高度）

// cur节点的最大深度，就是cur的高度
int getDepth(TreeNode* cur) {stack<TreeNode*> st;if (cur != NULL) st.push(cur);int depth = 0; int result = 0;while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();st.push(node);st.push(NULL);depth++;if (node->right) st.push(node->right);if (node->left) st.push(node->left);} else {st.pop();node = st.top();st.pop();depth--;}result = result > depth ? result : depth;}return result;
}

然后再用栈来模拟后序遍历，遍历每一个节点的时候，再去判断左右孩子的高度是否符合，代码如下:

bool isBalanced(TreeNode* root) {stack<TreeNode*> st;if (root == NULL) return true;st.push(root);while (!st.empty()) {TreeNode* node = st.top();st.pop();if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {return fasle;}if (node->right) st.push(node->right);if (node->left) st.push(node->left);}return true;
}

当然此题用迭代法，其实效率很低，因为没有很好的模拟回溯的过程，所以迭代法有很多重复的计算。

虽然理论上所有的递归都可以用迭代来实现，但是有的场景难度可能比较大。

例如：都知道回溯法其实就是递归，但是很少人用迭代的方式去实现回溯算法！

因为对于回溯算法已经是非常复杂的递归了，如果再用迭代的话，就是自己给自己找麻烦，效率也并不一定高。

代码实现

递归法

class Solution {
public:int getHeight(TreeNode* node) {if (node == NULL) return 0;int leftHeight = getHeight(node->left);if (leftHeight == -1) return -1;int rightHeight = getHeight(node->right);if (rightHeight == -1) return -1;return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftheight, rightHeight);}bool isBalanced(TreeNode* root) {return getHeight(root) == -1 ? false : true;}
};

迭代法

class Solution {
public:
class Solution {
private:int getDepth(TreeNode* cur) {stack<TreeNode*> st;if (cur != NULL) st.push(cur);int depth = 0; // 记录深度int result = 0;while (!st.empty()) {TreeNode* node = st.top();if (node != NULL) {st.pop();st.push(node);                          // 中st.push(NULL);depth++;if (node->right) st.push(node->right);  // 右if (node->left) st.push(node->left);    // 左} else {st.pop();node = st.top();st.pop();depth--;}result = result > depth ? result : depth;}return result;}public:bool isBalanced(TreeNode* root) {stack<TreeNode*> st;if (root == NULL) return true;st.push(root);while (!st.empty()) {TreeNode* node = st.top(); st.pop();if (abs(getDepth(node->left) - getDepth(node->right)) > 1) {return false;}if (node->right) st.push(node->right);           // 右（空节点不入栈）if (node->left) st.push(node->left);             // 左（空节点不入栈）}return true;}
};