LeetCode 977 有序数组的平方
本题思路:最容易想到的就是使用暴力循环的方式,将数组每个值都平方,然后进行一个排序操作。但是这样做,使用快排,它的复杂度也是 ologn。
所以,我们可以尝试用双指针的方法 :
一个 指针 left = 0,一个指针 right = nums.length-1。然后对比 nums[left] 和 nums[right]的大小,谁大,赋值给 result的数组,从result数组从下标 cur = nums.length-1 开始赋值。赋值完 cur-- 。 如果 nums[left] 大,则 left++, 如果 nums[right]大,则 right–。相等随便哪个都行。 最终 left>right 的时候,停止循环。
class Solution {public int[] sortedSquares(int[] nums) {int left = 0;int right = nums.length - 1;int cur = nums.length - 1;int[] result = new int[nums.length];while(left <= right){if(nums[left]*nums[left] < nums[right]*nums[right]){result[cur--] = nums[right] * nums[right];right--;}else{result[cur--] = nums[left] * nums[left];left++;}}return result;}
}
下面用一个图,来演示下测试用例的一个过程,以便更加直观的分析了解代码。

- 第一次循环,判断 nums[left] * nums[left] 和 nums[right]*nums[right] 大小,此时 nums[right]*nums[right] 大,则 将 result[cur] = nums[right]*nums[right],并且 cur–,right–。
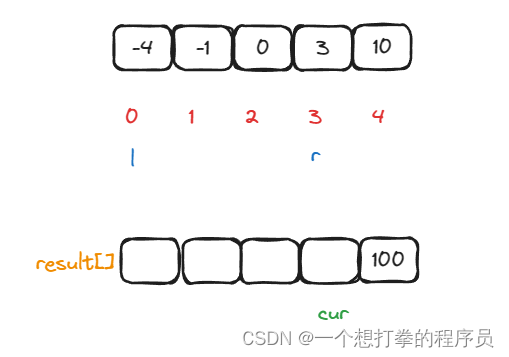
- 第二次循环,判断 nums[left] * nums[left] 和 nums[right]*nums[right] 大小,此时 nums[left]*nums[left] 大,则 将 result[cur] = nums[left]*nums[left],并且 cur–,left++。
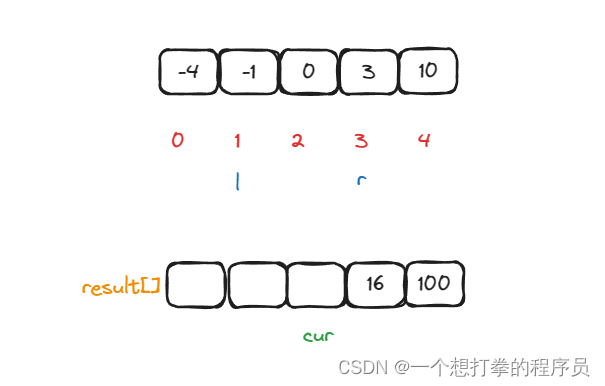
- 第三次循环,判断 nums[left] * nums[left] 和 nums[right]*nums[right] 大小,此时 nums[right]*nums[right] 大,则 将 result[cur] = nums[right]*nums[right],并且 cur–,right–。
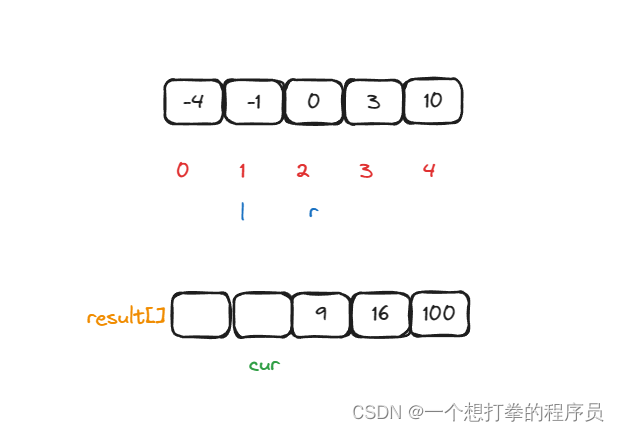
- 第四次循环,判断 nums[left] * nums[left] 和 nums[right]*nums[right] 大小,此时 nums[left]*nums[left] 大,则 将 result[cur] = nums[left]*nums[left],并且 cur–,left++。
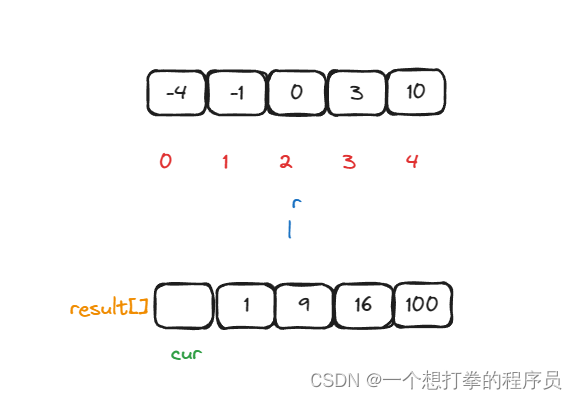
- 第四次循环,判断 nums[left] * nums[left] 和 nums[right]*nums[right] 大小,此时相等,则 将 result[cur] = nums[left]*nums[left],并且 cur–,left++。
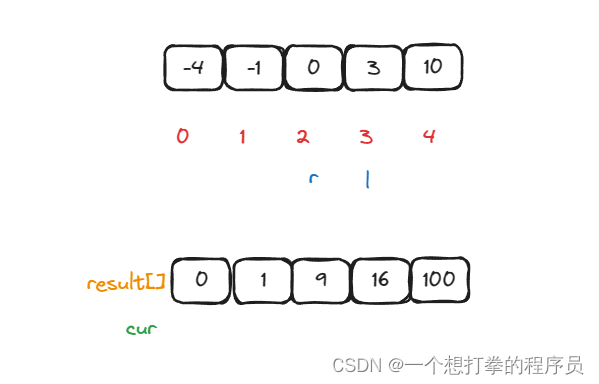
- 最后循环条件不能满足,终止。
LeetCode 209 长度最小的子数组
本题思路:使用滑动窗口的思想来解决这道题目,就用示例中的样例,来画个图分析以下思想。

- 初始状态下,i = 0, j = 0
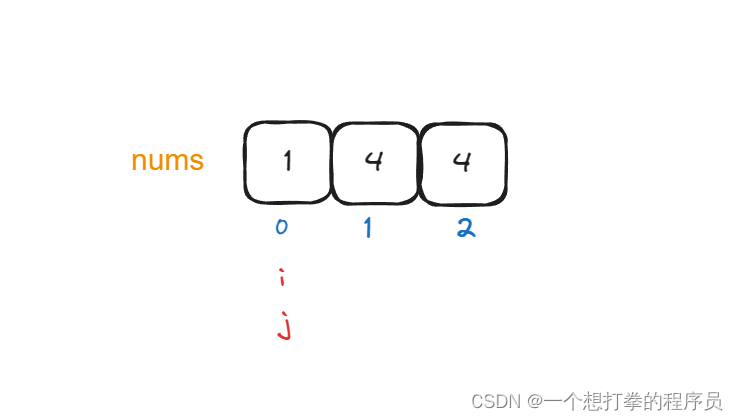
- 现在开始 j 向右滑动窗口,一直到找到 sum 的值 >= target 就停止
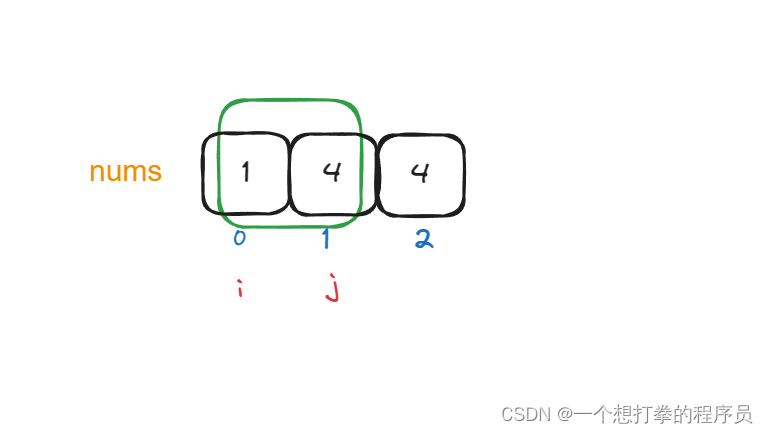
- 然后就应该,i 向右 缩减窗口大小,直至 sum < targer,为止,在这过程如果遇到了 sum = target 的情况,就记录下长度
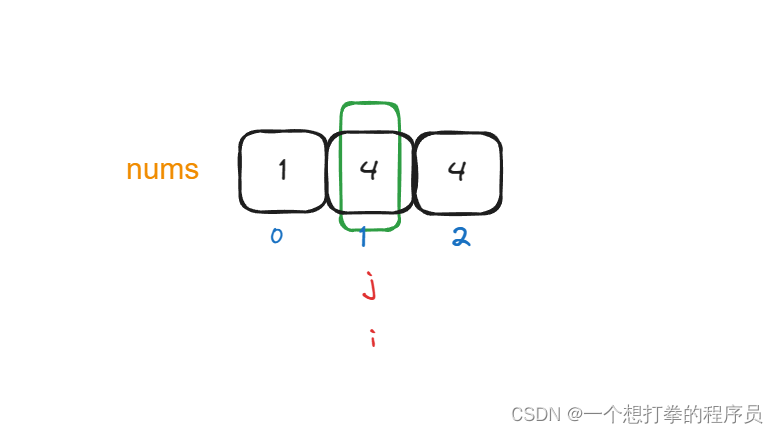
- 继续 i 往右边缩减窗口大小, 此时 sum < target, 就要开始 j 向右移动增加窗口的大小
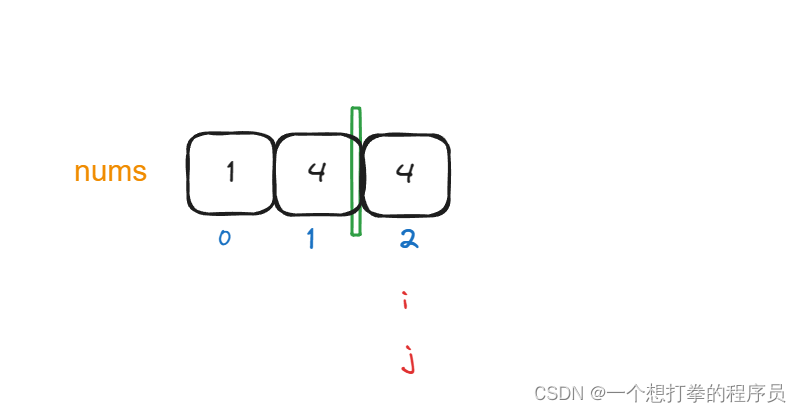
- 此时又相当于 回到了初始状态,i == j。 那么之间 j 走过的地方 就可能已经找到包含满足条件的 长度最小的子数组。接着继续往后找是否还存在。
这整一个查找的过程就相当于是一个 滑动的窗口,一直往后滑动,并没有往回查找。
class Solution {public int minSubArrayLen(int target, int[] nums) {int i = 0;int j = 0;int sum = 0;int minLen = Integer.MAX_VALUE;int len = 0;for(;j<nums.length;j++){// 如果 sum 值小于 target j++ 窗口向右扩展sum += nums[j];// sum > target就开始 i 向右 缩减窗口大小while(sum >= target){// 记录当前长度len = j - i + 1;if( len < minLen){minLen = len; }sum -= nums[i];i++; }}return minLen != Integer.MAX_VALUE?minLen:0;}
}
LeetCode 59 螺旋矩阵||
本题思路:就要在于这个边界的判断,此处我使用的是左闭右开的一个区间。如下图所示
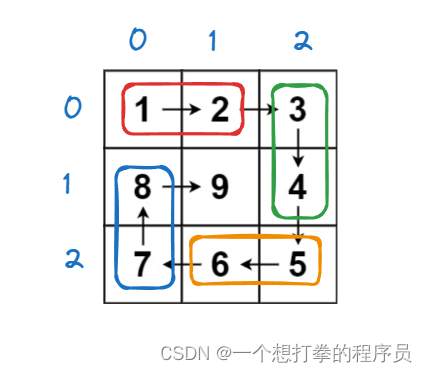
以上就是一圈,定义一个 staryx = 0, 一个starty = 0。用来表示起始位置,定义一个 i , 一个 j 来移动给数组赋值。依次从上侧(从左往右),从右侧(从上往下),从下侧(从右往左),从左侧(从下往上),对数组进行相应的赋值。 还有一个重点,就是考虑 i 和 j 的位置到哪里是 边界停止,就要设定一个 offset 偏移量,边界为 n- offset 。并且矩阵的大小跑完一圈,就相当于缩小了,所以 offset 也需要改变。
class Solution {public int[][] generateMatrix(int n) {int[][] result = new int[n][n];int startx = 0;int starty = 0;int i = 0;int j = 0;// 表示绕几圈,可以自己画个图,就知道规律了int loop = n / 2;int count = 1; // 用来给数组赋值int mid = n / 2; // 当 n 为奇数的时候,中间值的坐标就是 result[mid][mid]int offset = 1; // 表示偏移量// 使用左闭右开原则while(loop-- != 0 ){// 上侧 从左往后遍历 i不变, j变for(j = starty; j < n - offset; j++){result[startx][j] = count++;}// 右侧 从上往下遍历 j不变,i变for(i = startx; i < n - offset; i++){result[i][j] = count++;}// 下侧 从右往左遍历 i不变,j变for(; j > starty; j--){result[i][j] = count++;}// 左侧 从下往上遍历 j不变,i变for(; i > startx; i--){result[i][j] = count++;}// 转完一圈后startx++;starty++;offset++;}// 特殊情况,如果 n 为奇数,需要填充中间if(n % 2 == 1){result[mid][mid] = count;}return result;}
}
下面以下个示例,做个图来分析步骤,以便能理解代码的逻辑。
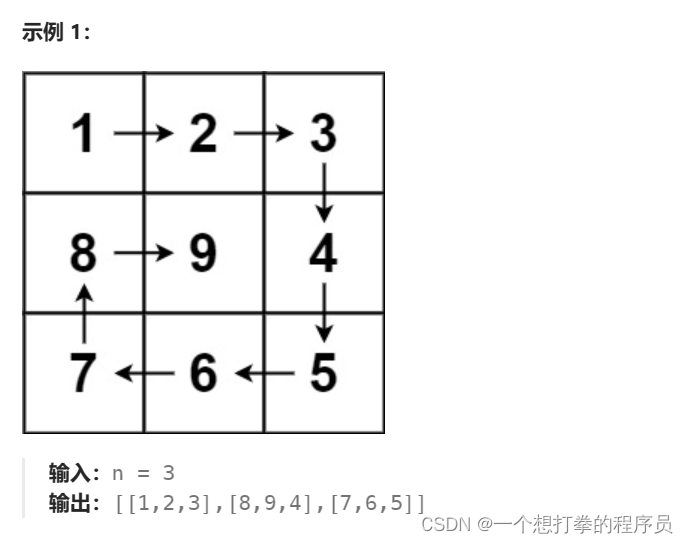
从题目中分析 ,n = 3 ,所以 顺时针旋转为 n/2=1 圈。 n - 1 = 3 - 1 = 2
- 上侧(从左往右)j < n - offset = 2
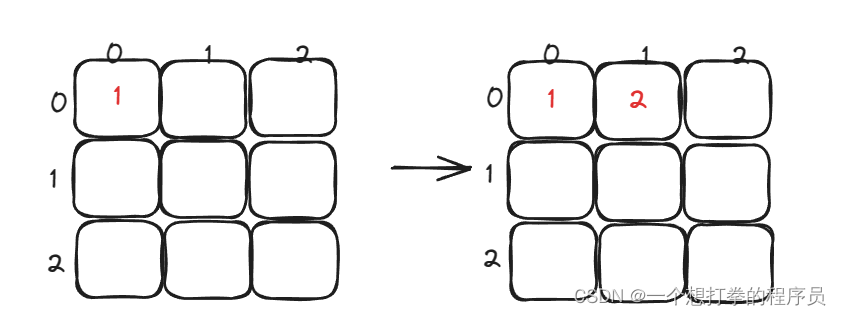
- 右侧(从上往下) i < n - offset = 2
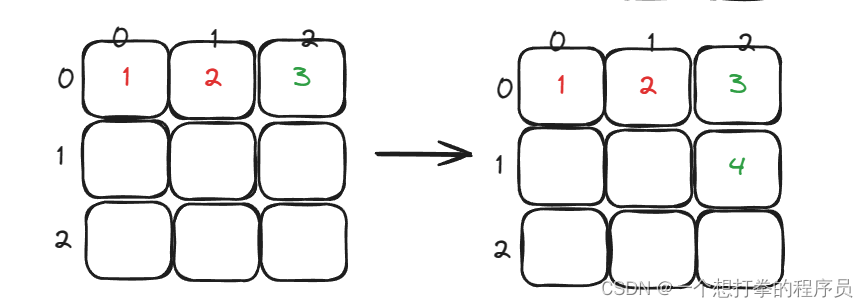
- 下侧(从右往左)j > startx=0
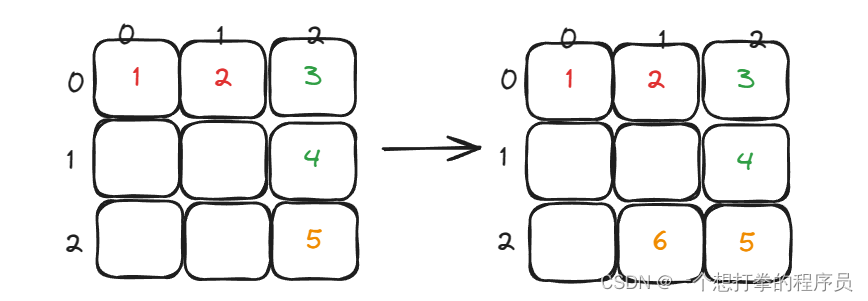
- 左侧(从下往上)i > startx=0
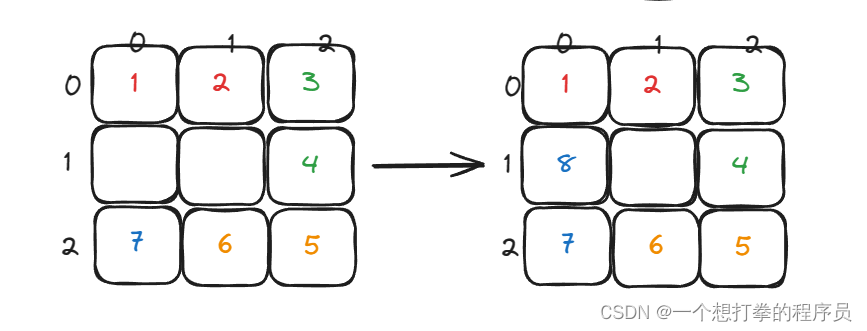
- 一轮循环结束,最后再将中间的值填充即可。