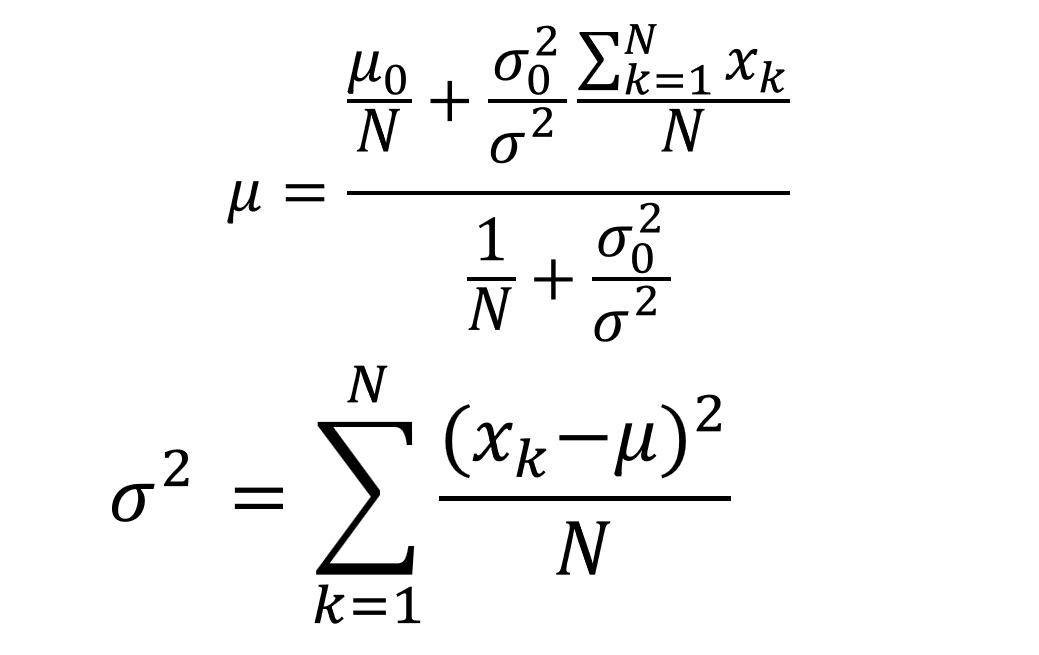例1:

解:
最大似然估计:
P (男) = 8 / 20 = 0.4 , P (女) = 12 / 20 = 0.6 P(男)= 8/20=0.4,P(女) = 12/20 = 0.6 P(男)=8/20=0.4,P(女)=12/20=0.6
a r g m a x ∏ i = 1 n ( P i ) = ln ∏ i = 1 n P i = ln ∏ i = 1 n 1 2 π ρ e x p ( − ( x i − μ ) 2 2 ρ 2 ) = n ln 1 2 π ρ − ∑ i = 1 n ( x i − u ) 2 2 ρ 2 argmax \prod _{i = 1} ^ n(P_i) = \ln \prod_{i=1}^n P_i = \ln \prod_{i=1}^n \frac{1}{\sqrt {2 \pi} \rho} exp(-\frac{(x_i - \mu)^2}{2\rho^2}) =\\ n \ln \frac{1}{ \sqrt {2 \pi } \rho} - \sum_{i=1}^n \frac{(x_i - u)^2}{2 \rho^2} argmaxi=1∏n(Pi)=lni=1∏nPi=lni=1∏n2πρ1exp(−2ρ2(xi−μ)2)=nln2πρ1−i=1∑n2ρ2(xi−u)2
对u求导并令导数为0得:
∑ i = 1 n ( x i − u ) ρ 2 = 0 \sum_{i=1}^n \frac{ (x_i - u) }{\rho^2}= 0 i=1∑nρ2(xi−u)=0
即:
1 n ∑ i = 1 n x i = μ \frac{1}{n}\sum _{i=1}^nx_i = \mu n1i=1∑nxi=μ
同理可得:
ρ 2 = 1 n ∑ i = 1 n ( x i − u ) 2 \rho ^2 = \frac{1}{n} \sum_{i=1}^n (x_i - u)^2 ρ2=n1i=1∑n(xi−u)2
例2:

解:
例3:

解:
公式: