目录

2415. 反转二叉树的奇数层

题目描述：

实现代码与解析：

BFS

原理思路：

---

2415. 反转二叉树的奇数层

题目描述：

        给你一棵 完美 二叉树的根节点 root ，请你反转这棵树中每个 奇数 层的节点值。

• 例如，假设第 3 层的节点值是 [2,1,3,4,7,11,29,18] ，那么反转后它应该变成 [18,29,11,7,4,3,1,2] 。

反转后，返回树的根节点。

完美 二叉树需满足：二叉树的所有父节点都有两个子节点，且所有叶子节点都在同一层。

节点的 层数 等于该节点到根节点之间的边数。

示例 1：

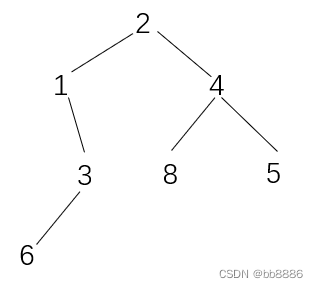
输入：root = [2,3,5,8,13,21,34]
输出：[2,5,3,8,13,21,34]
解释：
这棵树只有一个奇数层。
在第 1 层的节点分别是 3、5 ，反转后为 5、3 。

示例 2：

输入：root = [7,13,11]
输出：[7,11,13]
解释： 
在第 1 层的节点分别是 13、11 ，反转后为 11、13 。 

示例 3：

输入：root = [0,1,2,0,0,0,0,1,1,1,1,2,2,2,2]
输出：[0,2,1,0,0,0,0,2,2,2,2,1,1,1,1]
解释：奇数层由非零值组成。
在第 1 层的节点分别是 1、2 ，反转后为 2、1 。
在第 3 层的节点分别是 1、1、1、1、2、2、2、2 ，反转后为 2、2、2、2、1、1、1、1 。

提示：

• 树中的节点数目在范围 [1, 214] 内
• 0 <= Node.val <= 105
• root 是一棵 完美 二叉树

实现代码与解析：

BFS

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode reverseOddLevels(TreeNode root) {Queue<TreeNode> q = new LinkedList<>();q.offer(root);boolean flag = false;while (!q.isEmpty()) {int size = q.size();List<TreeNode> arr = new ArrayList<>();for (int i = 0; i < size; i++) {TreeNode t = q.peek();q.poll();if (flag) arr.add(t);if (t.left != null) {q.offer(t.left);q.offer(t.right);}}if (flag) {for (int i = 0, j = size - 1; i <j; i++, j--) {int tmp = arr.get(i).val;arr.get(i).val = arr.get(j).val;arr.get(j).val = tmp;}}flag ^= true; // 不同时为真}return root;}
}

原理思路：

        简单的层次遍历，若为奇数层，则放入arr中，遍历完后，反转值。

此题深度从0开始，而且注意是反转值，而不是结点。