654. 最大二叉树

思路:这道题的目的是从给定的nums数组中找到一个最大值当做二叉树的根节点,然后以最大值左右两边的元素分别构建二叉树。也就是一个左中右的顺序,所以构建二叉树这种题用前序遍历是再合适不过了,因为根节点把左右子树分开了,很好分辨。
这里我们用for循环去记录当前最大值的index,如果index>0的话,那么就从nums[0:index]构建左子树,如果index<len(nums)-1,那么就从[index+1:]的位置到最后去构建右子树。然后分别递归
代码:
max_num = float('-inf')index =0for i in range(len(nums)):if nums[i] > max_num:max_num = nums[i]index = i #找到最大值 构建根节点root = TreeNode(max_num)if index>0:left = nums[0:index]root.left = self.constructMaximumBinaryTree(left)if index<len(nums)-1:right = nums[index+1:]root.right = self.constructMaximumBinaryTree(right)return root这里为什么要去判断index是不是大于0,经过刚才我的实验,我认为是如果我们的最大值在第一个元素也就是index= 0的时候,我们的左子树目前是不能构成的,那么就直接先构建右子树。
617. 合并二叉树

思路:本题和之前的反转二叉树有点类似,同时操作两个二叉树
判断条件:
当root1==none的时候,应该直接返回root2,
当root2==none的时候 应该直接返回root1
然后才是当两个都不为空的时候,root1.val+=root2.val构造新节点的值
这里重复用了tree1去构造新的二叉树,所以最后直接返回tree1就好了,然后就是合并之后继续递归当前的节点的左子树和tree2当前节点的左子树(注意 他们是同步进行操作的,并不是异步)可能有朋友问 你怎么知道tree1遍历到当前节点的时候,tree2刚好也在这个位置呢?这是因为他们两个是同时进行操作的 并不是先后遍历。
同理,当前节点的右子树也是递归。
代码:
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:if root1==None:return root2 if root2==None:return root1 root1.val+=root2.val root1.left = self.mergeTrees(root1.left,root2.left)root1.right = self.mergeTrees(root1.right,root2.right)return root1700. 二叉搜索树中的搜索

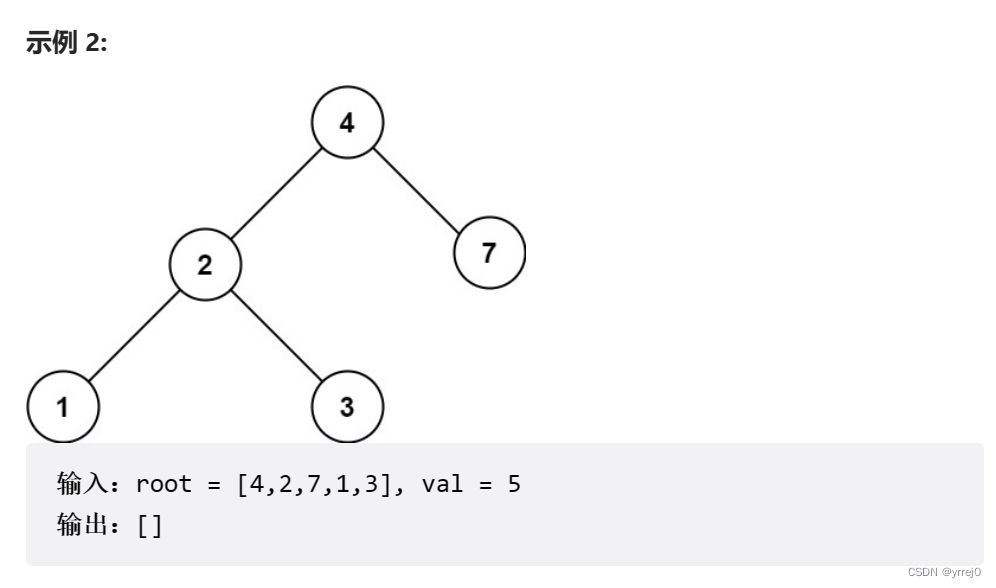
二叉搜索树特性:中序遍历为有序数组
如果当前root的值小于寻找的值,那么肯定不在我们的左子树,一定是去右子树找
同理,如果当前值大于寻找值,也一定去左子树找。
这里递归的终止条件:直到我们找到当前root的值等于寻找值,那么就直接返回root
递归参数:root
单层循环逻辑:if root.val > val:
return self.traversal(root.left)
if root.val <val:
return self.traversal(root.right)
代码:
def searchBST(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:#这里注意一个特性 二叉搜索树 中序遍历为有序数组 if not root:return Noneif root.val==val:return rootif root.val<val:return self.searchBST(root.right,val)if root.val>val:return self.searchBST(root.left,val)