EM算法

简介

EM算法的核心分为两步

1. E步（Expection-Step）
2. M步（Maximization-Step）

因为在最大化过程中存在两个参量$r,\theta$，其中若知道$r$，则知道$\theta$；若知道$\theta$，则知道$r$。且两个量未存在明显的关系，但又互相依存可以采用EM算法

其中主要思想为：

1. 首先随机初始化参数$r$
2. 然后求的在参数$r$下按照极大似然估计求得参数$\theta$
3. 然后根据参数$\theta$按照极大似然估计求得参数$r$
4. 循环至收敛

算法示例

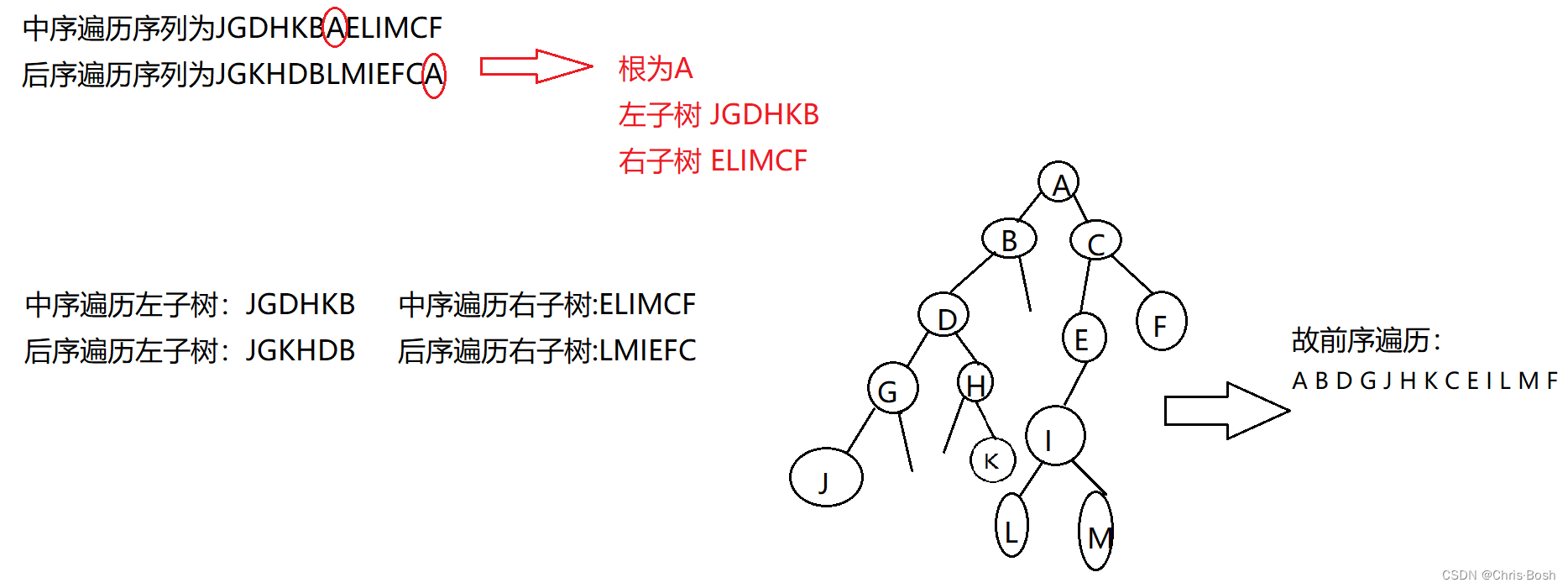
如下图所示存在A，B两种硬币，其中抛出正反面的概率未知，其中H表示正面，F表示反面

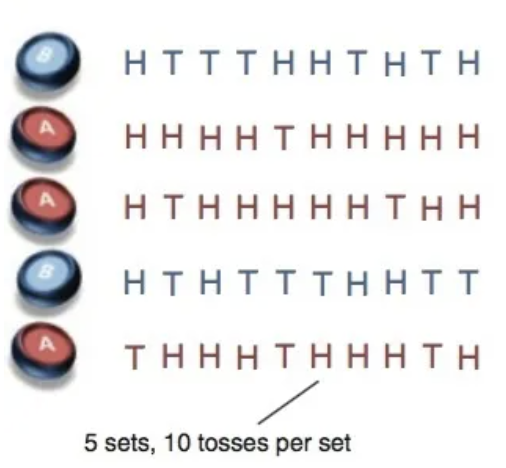
根据统计可得

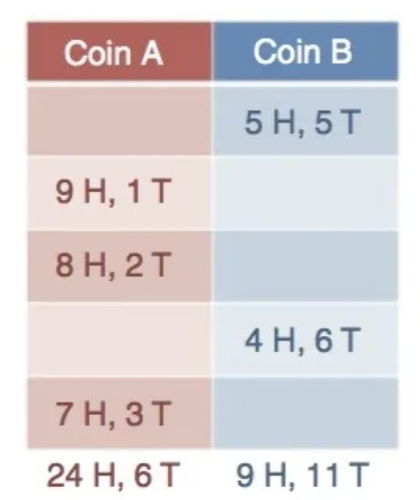
可得
$$\begin{gathered} P(H|X=A)=\frac{24}{24+6}=0.8 \\ P(H|X=B)=\frac{9}{9+11}=0.45 \end{gathered}$$
若更改条件，不知道此时抛出是哪一枚硬币，只知道抛出的结果，即

首先初始化，设
$$\begin{gathered} P(H|X=A)=0.6 \\ P(H|X=B)=0.5 \end{gathered}$$
若当抛出的第一枚硬币为A时

此时的出现该情况的概率为$P_1(A)=0.6^5\ast (1-0.6{)}^5=0.0007962624$

若当抛出的第一枚硬币为B时

此时的出现该情况的概率为$P_1(B)=0.5^5\ast (1-0.5{)}^5=0.0009765625$

其中
$$\begin{gathered} P^1(A)=\frac{P_1(A)}{P_1(A)+P_1(B)}\approx 0.45 \\ {P}^1(B)=\frac{P_1(B)}{P_1(A)+P_1(B)}\approx 0.55 \end{gathered}$$
同理可得
$$\begin{gathered} P^2(A)\approx 0.80,P^2(B)\approx 0.20 \\ {P}^3(A)\approx 0.73,P^3(B)\approx 0.27 \\ {P}^4(A)\approx 0.35,P^4(B)\approx 0.65 \\ {P}^5(A)\approx 0.65,P^5(B)\approx 0.35 \end{gathered}$$
设第2，3，5轮抛出的为硬币A，第1，4轮抛出的为硬币B，可得
$$\begin{gathered} P(H|X=A)=\frac{9+8+7}{30}=\frac{24}{30}=0.8 \\ P(H|X=B)=\frac{5+4}{20}=\frac{9}{20}=0.45 \end{gathered}$$
由此循环直至收敛