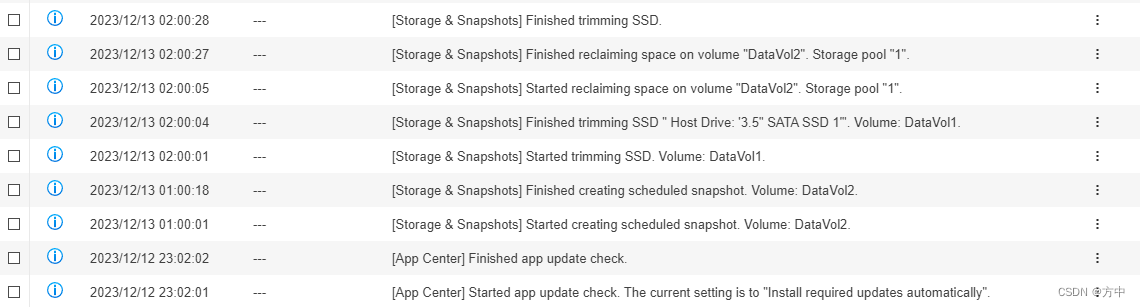
51. N 皇后

应为各个皇后之间不能同行,所以一行只能有一个皇后。我们可以遍历每一行的各个位置,判断该位置是否可以放置皇后,一行放置一个。当一个皇后的位置已经在这一行确定了,我们就可以遍历下一行来确定下一个皇后在下一行的位置,是不是像是在不同集合里各取一个数。和17.电话号码的字母组合 类似,只不过这题在取值的时候是有条件的。在不同集合间取值是不需要startIndex(开始位置)的。
class Solution {
public:vector<string> path;vector<vector<string>> ans;bool isEffective(vector<string> path, int depth,int index){if(depth==0) return true;//检查同一列是否有皇后for(int i=0;i<path.size();i++){if(path[i][index]=='Q') return false;}//检查左上方是否有皇后int d=depth-1,j=index-1;while(d>=0 && j>=0 && j<path[0].size()){if(path[d][j]=='Q') return false;d--;j--;}//检查右上方是否有皇后d=depth-1;j=index+1;while(d>=0 && j>=0 && j<path[0].size()){if(path[d][j]=='Q') return false;d--;j++;}return true;}void backtracking(int n,int depth){//当确立了n个皇后,收集结果if(path.size()==n){ans.push_back(path);return;}for(int i=0;i<n;i++){//检查当前索引是否可行if(!isEffective(path,depth,i)) continue;//回溯string temp(n,'.');temp[i]='Q';path.push_back(temp);backtracking(n,depth+1);path.pop_back();}}vector<vector<string>> solveNQueens(int n) {backtracking(n,0);return ans;}
};37. 解数独

还是需要用回溯,用两层for循环来确定位置。然后在该位置处遍历1-9,判断合适的数字。遇到合适的数字后就将其写入board中,然后利用递归再对下一个空白处进行值的确定。
class Solution {
public://判断值是否合适bool isOK(vector<vector<char>>& board,char c,int row,int list){for(int i=0;i<board.size();i++){//检查行if(board[row][i]==c) return false;//检查列if(board[i][list]==c) return false;}//检查九宫格for(int i=(row/3)*3;i<(row/3)*3+3;i++){for(int j=(list/3)*3;j<(list/3)*3+3;j++){if(board[i][j]==c) return false;}}return true;}bool backtracking(vector<vector<char>>& board){for(int i=0;i<board.size();i++){for(int j=0;j<board.size();j++){//判断该位置是否为空if(board[i][j]=='.'){//遍历1-9,寻找符合条件的数字for(char c='1';c<='9';c++){if(isOK(board,c,i,j)){board[i][j]=c;//递归下一层,确定下一个空白处的值bool b=backtracking(board);//如果返回true,说明board中所有的值都已经被确定了if(b) return true;board[i][j]='.';}}return false;}}}return true;}void solveSudoku(vector<vector<char>>& board) {backtracking(board);}
};