地球坐标系介绍--地心大地、地心地固直角、协议地球坐标系-编程知识

在研究地面点间几何关系的问题中，一般使用地球坐标系。地球坐标系固定在地球上，它跟随地球自转而不断地运动，相对地球却不存在运动，因此，地球坐标系也称地固坐标系。所有和地球保持固定关系的点，如地面点，它们在地球坐标系中的坐标值是不变的，在地球坐标系中研究它们之间的几何关系是方便的。地球坐标系往往与人们的日常生活紧密相关，也较容易理解。

1.大地水准面和地球椭球

1.1大地水准面

地球表面起伏不习数学模型来描袭的典面述这样一个曲面是不现实的。
由于海洋面积占地球总面积的 71% ，人们就想到，用一个与处于流体静平衡状态的海洋面重合并延伸到大陆内部的水准面作为地球表面的模型，称为大地水准面。
大地水准面的形状和大小是最接近于地球真实形状和大小的。
大地水准面上的重力处处相等并与其上的重力方向处处正交。
由于地面起伏不平和地球内部物质分布不均匀，各点的重力方向产生不规则的变化。因此，大地水准面的形状和重力场都是不规则的。所以，大地水准面不能用一个简单的几何形状和数学公式来表述。

1.2地球椭球

为了建立统一的、精密的地球坐标系，人个自然要寻求一个在形状和大小上与大地体非常接近，并且与大地体有着固定关系的数学体来代替大地体，作为建立地球坐标系的基准。

能模拟地球的最简单的数学体是旋转椭球体，称为地球椭球。

旋转椭球的短半轴与地球自转轴重合，长半轴的大小与赤道半径相等。
描述地球椭球几何特性 ( 形状和大小 ) 的参数有两个，即通常采用的椭球长半轴 a 和扁率 f 。扁

率 f 与长半轴 a 、短半轴 b 的关系为
长半轴 a 和扁率 f 仅反映地球椭球的几何特性。为研究地球的物理特性，还必须有物理参数
国际上明确规定采用以下四个参数来综合表示地球椭球的几何和物理特性，即地球椭球的长半轴 a 、引力常数与地球质量的乘积 GM (通常用 μ 来表示) 、地球重力场二阶带谐系数 J 2 、地球自转角速度 ω 。由此 4 个参数，可导出地球椭球的其他参数。

2.地心大地坐标系

地心大地坐标系采用的地球椭球的定义：地球椭球的中心与地球质心重合，椭球的短轴与地球自转轴重合，球的起始子午面与格林尼治子午面重合。定位结果所表示的经度、纬度就是在这个坐标系下的。因此，地心大地坐标系是卫星导航定位中应用最为广泛的坐标系。
经度和纬度是定位中常用的坐标。除了经纬度，我们还会关心另外一个维度——高程。
- 关于高程，有几个相近的概念容易混淆，即大地高、正常高和正高
  - 地面一点 P 的大地高 H 是由该点沿椭球法线到椭球面的距离
  - 正高 Hg 是由该点沿铅垂线到大地水准面的距离
  - 正常高 Hγ 是沿铅垂线到似大地水准面的距离
  - 其中，似大地水准面是大地水准面的一个近似。似大地水准面在海洋面与大地水准面吻合，而在陆地部分则与大地水准面略有差异。
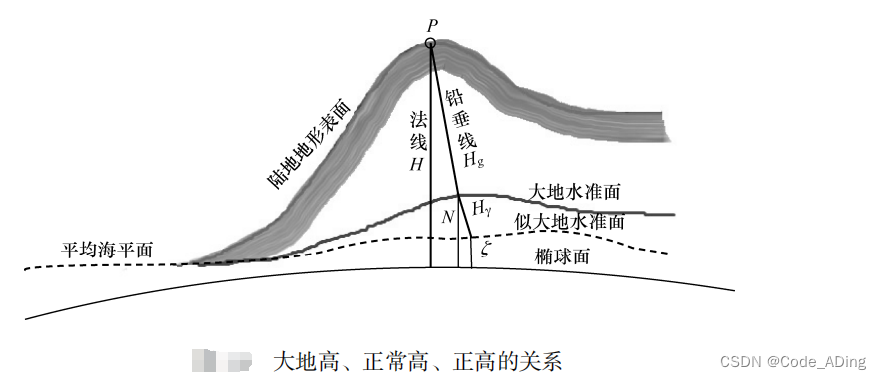
  - 严格来讲，法线与铅垂线方向不一致，但二者差异很小，在实用上可忽略不计。
  - 由上图可知：
  - 其中， N 为大地水准面至椭球面的距离，称为大地水准面差距或大地水准面高；ζ 为似大地水准面至椭球面的距离，称为高程异常。高程异常通常用天文水准或天文动水准方法求得。

3.地心地固坐标系

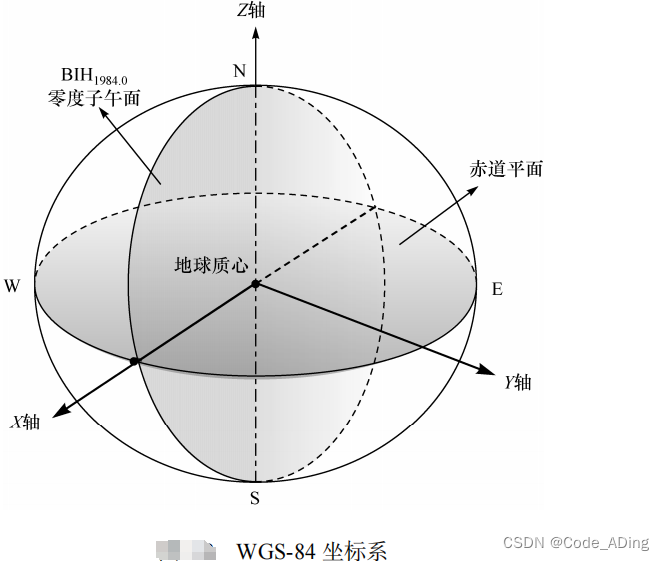
地心地固直角坐标系，简称为地心地固坐标系，其定义是: 原点 O 与地球质心重合，Z 轴与地球自转轴重合并指向北极，X轴指向格林尼治子午面与赤道面的交点，Y轴垂直于 XOZ 平面并与 X、Z 轴构成右手坐标系。任意一点的位置用(x,y.z)坐标表示。
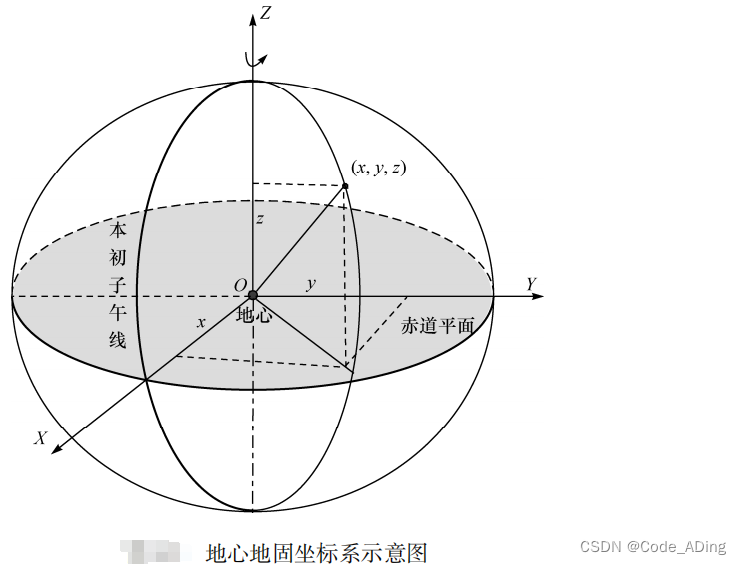
- 虽说用 ( x， y， z） 表示地球上点位的坐标不如经度、纬度和高程那么直观，但是对于求两点之间的距离、两点间的角度关系等数学运算却很方便，因此导航定位方程中，用户和卫星的坐标都采用该坐标系描述。

3.1地心大地坐标转换成地心地固直角坐标

已知某一点 P 的大地纬度 B、经度 L和高度 H，计算该点的地心地固直角坐标(x,y,z)转换公式如下。
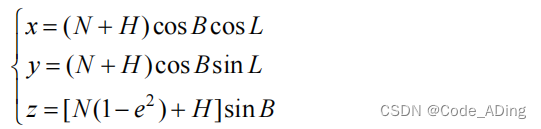
- 其中， N 为参考椭球的卯酉圈曲率半径，即
  - a 为参考椭球长半轴； e 2 为参考椭球第一偏心率平方。
  - 若已知参考椭球的扁率 f ， e 2 也可由 f 计算，即：

3.2地心地固直角坐标转换成地心大地坐标

已知某一点 P 的地心地固直角坐标(x， y， z） ，计算该点的地心大地坐标(B，L，H) ，转换公式如下。
- ·其中， N 和e 2 分别由3.1中的公式计算得到。
- 计算大地纬度 B 时，由于公式中含有待求量 B ，因此需要进行迭代计算。但由于e 2 是一个小量，因此收敛很快。迭代步骤如下。
  - (1) 由于e 2 是一个小量，可以先将其忽略，得到初始值 B0
  - (2) 将 B 0 分别代入，得到 N 和 B 1
  - 上述迭代一般只需进行 3～4 次循环即可收敛。收敛后，再将大地纬度 B 代入公式，即可得到准确的参考椭球的卯酉圈曲率半径 N 。
- 需要注意的是，计算高程 H 需要用到大地纬度 B 和参考椭球的卯酉圈曲率半径 N ，因此在计算得到大地纬度 B 和参考椭球的卯酉圈曲率半径 N 之后，方可计算高程 H，经度 L的计算则不受此限制。

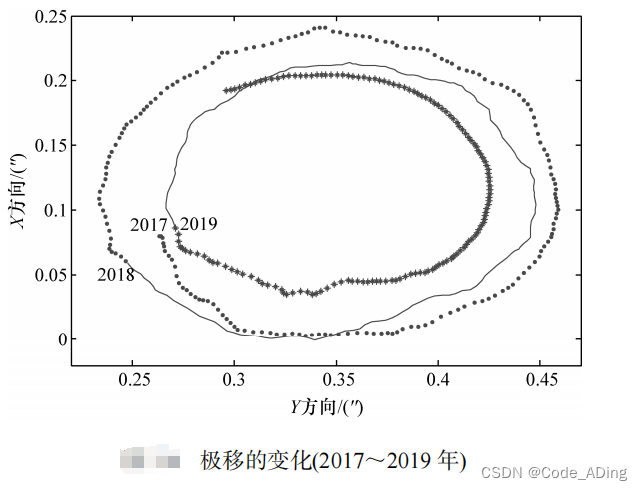
4.地级移动

地球自转轴相对于地球并不是固定不变的，地球南北两个极点在地球表面以每年几米的速度大致沿一个半径十几米的小圆移动。这种运动称为地极移动，简称极移。
由于极移将使地球自转轴的轴向发生变化，因此根据地球自转轴所定义的地球坐标系也将发生变化，这将给实际工作造成许多困难。为了解决这一问题，通常选定某一固定的平极来建立地球坐标系。 1967年国际天文学联合会 (IAU) 和国际大地测量协会 (IAG) 联合确定将 1900 ～ 1905 年地极位置的平均值作为地极坐标系的原点，称为国际协议原点(Conventional International Origin, CIO) ，也称为协议地极 (conventional terrestrial pole, CTP) 。与协议地极相对应的地球赤道称为平赤道或协议赤道面。
1968 年国际时间局 (Bureau International de IˊHeure, BIH) 决定将通过国际习用原点和格 林尼治天文台的子午线作为起始子午线，该起始子午线与协议赤道面的交点作为经度零点。故该起始子午线称为 BIH 零子午线，它是与协议地极相对应的。
1988 年，国际大地测量与地球物理学联合会 (IUGG) 和国际天文学联合会建立了国际地 球自转服务(IERS) ，用以取代国际时间局的地球自转服务部分以及原有的国际极移服务 (IPMS)。IERS 的职能之一就是为当前应用和长期研究提供及时准确的地球定向参数 (EOP) 。

5.协议地球坐标系

协议地球坐标系(conventional terrestrial system, CTS) 是以协议地极定义的坐标系，其坐

标系原点在地球质心， Z 轴指向地球的协议地极， X 轴指向 BIH 经度零点， Y 轴与 X 、 Z 轴

构成右手坐标系。协议地球坐标系也是地心地固坐标系的一种。
以协议地极和 BIH 经度零点来定义的地心地固坐标系通常都是协议地球坐标系。卫星 导航系统的参考坐标系一般采用协议地球坐标系，如美国 GPS 采用 WGS-84 坐标系，中国 北斗卫星导航系统采用 CGCS2000 坐标系，即 2000 国家大地坐标系。

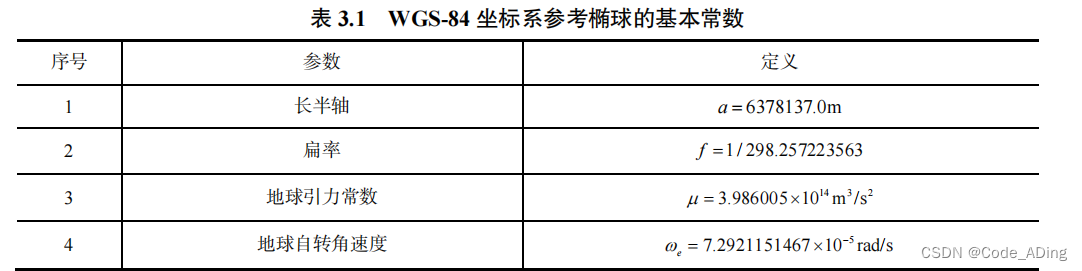
5.1 WGS-84坐标系

GPS 定位结果是在 WGS-84 坐标系中给出的。WGS-84 使用 BIH 定义的 1984.0 年新纪元参考框架，其坐标系原点定义于地球质心，Z 轴指向 BIH1984.0协议地极，X 轴指向 BIH1984.0的零子午面和 CTP 相应赤道的交点，Y 轴与 X、Z 轴构成右手坐标系

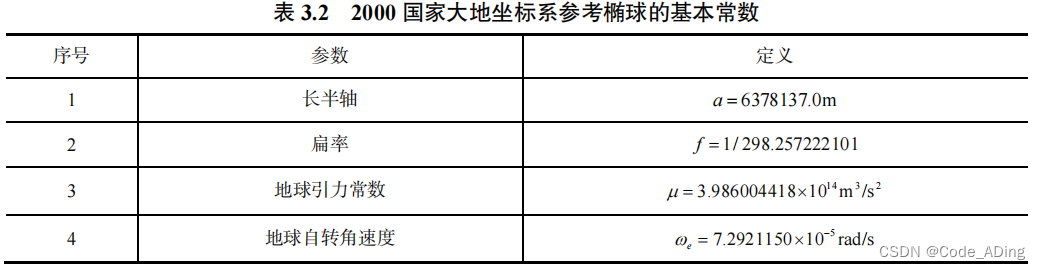
5.2 2000国家大地坐标系（ CGCS2000）

2000 国家大地坐标系(China Geodetic Coordinate System 2000，CGCS2000)的原点为包括海洋和大气的整个地球的质量中心，Z 轴由原点指向历元 2000.0 的地球参考极。
该历元的指向由国际时间局给定的历元 1984.0 作为初始指向来推算，定向的时间演化保证相对于地壳不产生残余的全球旋转；
- X 轴由原点指向格林尼治参考子午线与地球赤道面(历元2000.0)的交点；
- Y 轴与 Z 轴、X 轴构成右手坐标系。
历元 2000.0 的地球参考极及其对应的赤道面与 IERS 定义的一致，因此，也称为 IERS 参考极(IRP)和 IERS 参考子午面(IRM)

6.地固坐标系之间的转换

不同的地固坐标系采用不同历元的协议地球坐标系，可能会导致同一个点位在不同坐标系中取值略有差别。因此，需要建立不同坐标系之间的转换关系。
坐标转换模型很多，目前广泛使用的地固坐标系转换模型是布尔莎(Bursa)模型。
该模型中，所有地固坐标系之间的转换都可以通过 7 个参数进行转换：3 个平移参数、3 个旋转参数和 1 个尺度因子(坐标尺度定义不一致引起的改正数)
转换过程如下面图所示：
下面以 WGS-84 坐标系与 CGCS2000 坐标系转换为例，说明地固坐标系之间转换参数

的取值情况。
- 在定义上，CGCS2000 坐标系与 WGS-84 是一致的，即坐标系原点、尺度、
  
  定向及定向演变的定义都是相同的。比较可知，两个坐标系使用的参考椭球也非常接近，只有扁率有微小差异。
- 但因 CGCS2000 坐标系的坐标定义在 2000 年那一时刻，而大多数应用实际上是不同时 间进行定位的，且地球上的板块是在不断运动的，不同时刻位于地球不同板块上站点的实 际位置是在变化的，已经偏离了 2000 年的位置。因此不同时间定位得到的坐标不是严格意义下的 CGCS2000 坐标系。