1.NN的局限性
- 拓展性差
- NN的计算量大性能差,不利于在不同规模的数据集上有效运行
- 若输入维度发生变化,需要修改并重新训练网络
- 容易过拟合
- 全连接导致参数量特别多,容易过拟合
- 如果增加更多层,参数量会翻倍
- 无法有效利用局部特征
- 输入数据需要展平成一维,丢弃了图像等数据中的二维结构信息
- 相邻层完全连接,关注的是全局,没有关注局部区域
- 不具有平移不变性
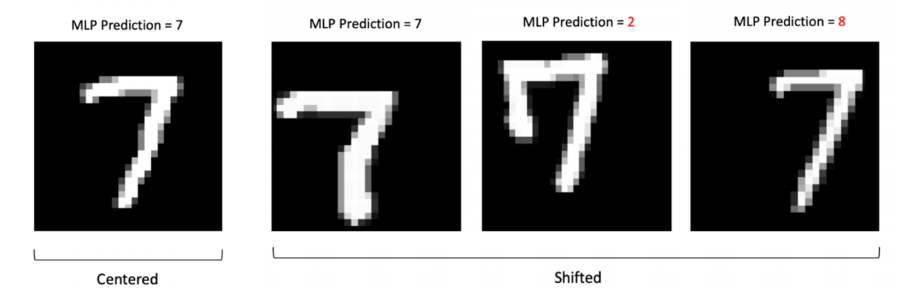
- 信息位置变换时,识别率就大幅降低
2.CNN的优势
• 大大降低过拟合的风险
• 利用数据中的局部结构
• 局部结构比全局特征具有更好的泛化能力
• 许多有用信息局限于局部区域
• 提高神经网络的鲁棒性
• 平移不变性:位置的改变不会改变输出
CNN常用于图像任务中
3.卷积
3.1 卷积操作
CNN的核心部分在于卷积操作,其使用卷积过滤器/卷积核(convolution filters/kernels)。通过卷积操作可以实现特征提取。
卷积操作如何实现?假设有一个5×5输入图像,使用一个3×3的卷积核(具体参数是什么意思会在后面介绍,这里不关键),卷积核参数如图。
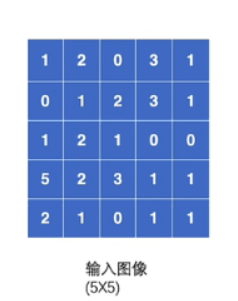

然后卷积核在输入图像上从左上角开始,从左到右,从上到下移动,每次移动一格,如果移动到右边位置不够一个卷积核大小则换行,如果移动到下面位置不够则直接结束,对应位置相乘相加再加上偏置项(可选)便是卷积后的输出
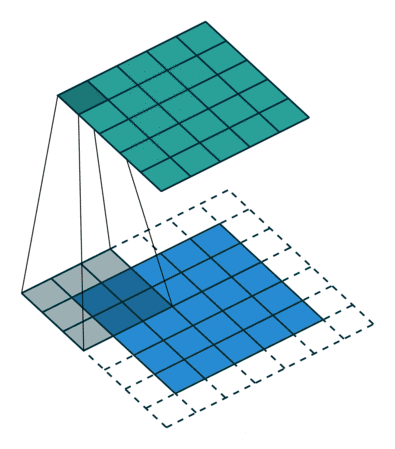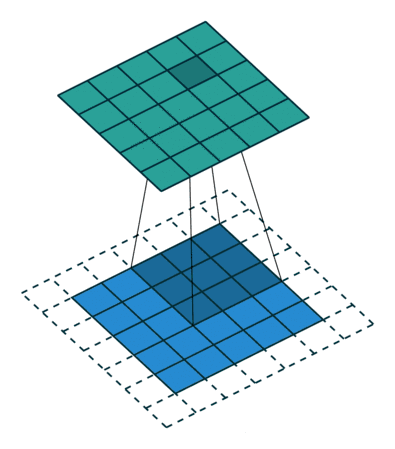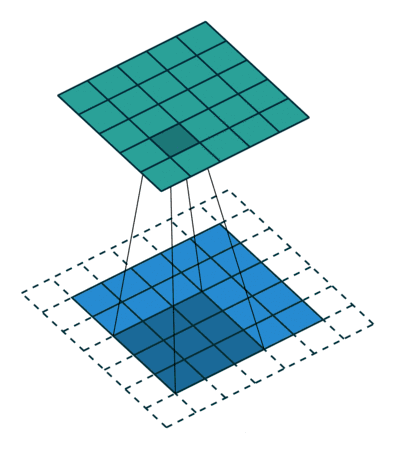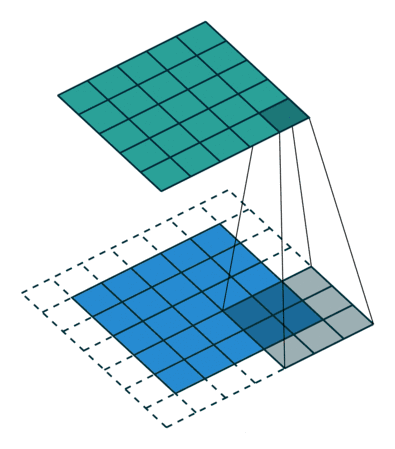

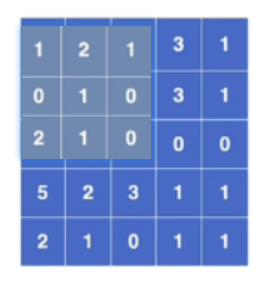

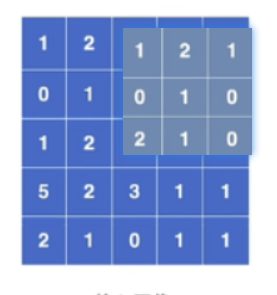
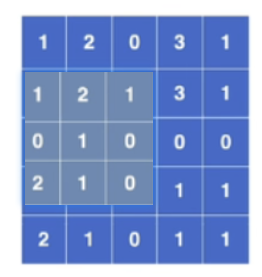
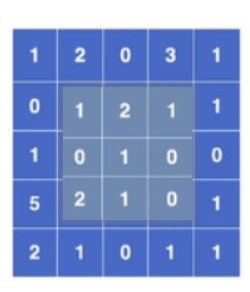
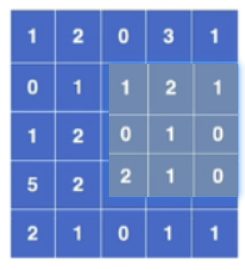 滑动6次后,下面已经不够位置了,卷积结束
滑动6次后,下面已经不够位置了,卷积结束
这里给出第一行怎么算出来的
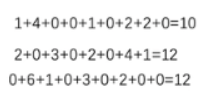
使用不同参数的卷积核可以达到不一样的效果

同样的在卷积操作后会使用激活函数
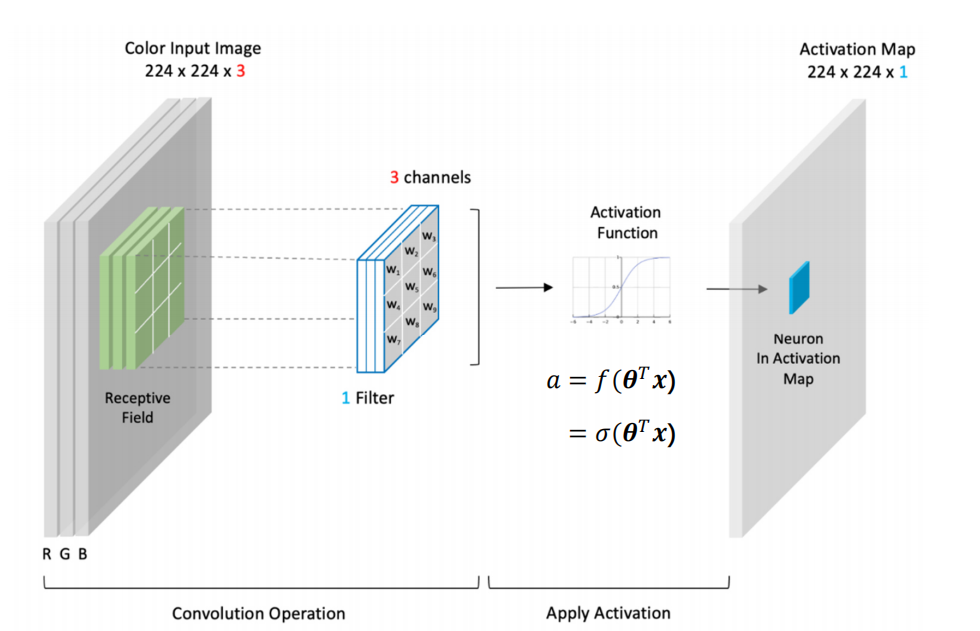
每一个数据点均经过激活函数进行非线性变换
3.2 卷积核
卷积核包括如下几个参数
- 卷积核大小:w×h,更大的卷积核会使输出尺寸更加小。常使用的有1×1,3×3,5×5,7×7。
- 步长stride:卷积核每次滑动多少格。步长可以成倍的减少输出尺寸。
- 输入通道数in_channels:就是输入数据是多少张叠加的,例如RGB图片就由R,G,B三通道合成的。输入通道为多少,就会使用多少个相同卷积核,分别对各个通道进行卷积,然后对应位置相加合成一个通道输出
- 输出通道数out_channels:通过卷积可以生成多少个通道特征图,使用多少组卷积核就可以生成多少个输出通道。
- 填充padding:在四周填充0像素的宽度,可以增大输出的尺寸。同时也可以解决常常丢失边缘像素的问题
所以在1.的例子中,完整的描述应该是输入图像大小为5×5,通道数为1,设定卷积核大小为3×3,步长为1,输入通道数和输出通道数都为1,填充为0。
——卷积核上的权重参数同样通过训练学习而得,他就是CNN的神经元。
——输入的位置信息嵌入到特征通道中
——在一次卷积中不同位置用的都是同一个卷积核,只是它在移动的,因此输出共享权重,因此
显著减少参数数量
——卷积核每次都会卷积一个局部区域,因此它可以在数据中查找局部结构
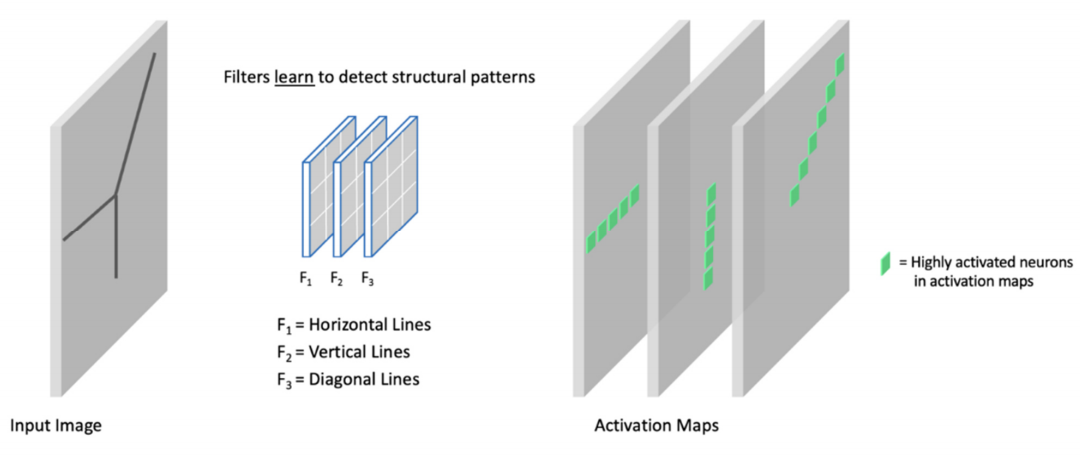
——使用多个卷积核,每个卷积核都会专注于输入数据的不同属性,从而生成不同的特征
…………………………………………………………………………………………………………………
几个关于通道数的例子
1.输入通道数为3。设置卷积核大小为3×3,输入通道数为3,输出通道数为1,使用三个卷积核

2.输入通道数为3。设置卷积核大小为3×3,输入通道数为3,输出通道数为4。会使用4组每组3个卷积核。
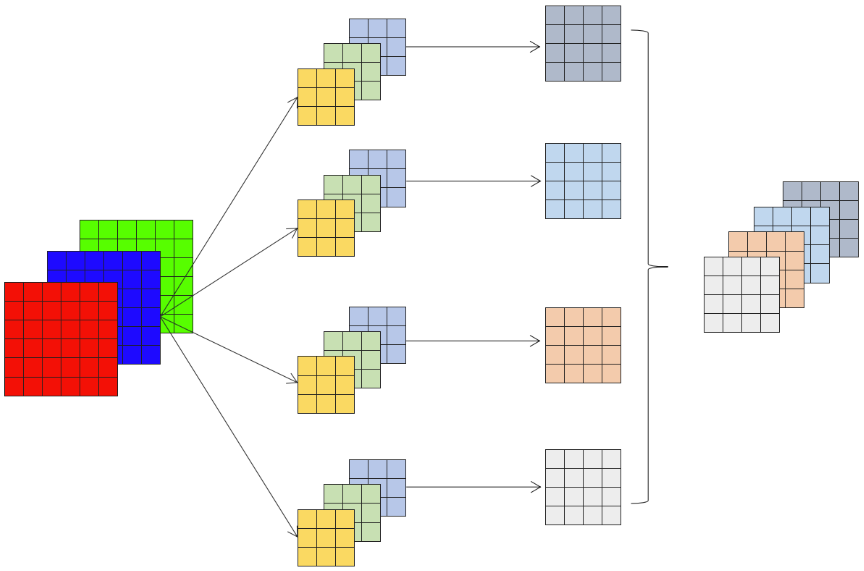
3.输入通道数为1。设置卷积核大小为3×3,输入通道数为1,输出通道数为3。会使用3组每组1个卷积核。

将所有这些通道堆叠在一起,我们可以得到一个特征图。
…………………………………………………………………………………………………………………
如何计算输出尺寸
卷积层输出大小 = (输入图像大小 - 卷积核大小 + 2 × 填充数) ÷ 步幅大小 + 1
output = (input - kernel_size + 2padding) / stride + 1
如果输入宽高可以被步幅整除,那么
output = input / stride
4.池化
池化同样会使用一个核,然后滑动,但这个核不带权重参数。池化层不会改变通道数,常用于减小特征图的尺寸。
其参数如下:
1.卷积核大小
2.步长
3.填充
输出尺寸计算同卷积操作。当有多个输入通道数,会对每一个输入通道进行池化操作然后合并输出通道只有一个
池化层的作用:
- 下采样(减少尺寸)减少过多的信息。这也会导致信息丢失
- 增加额外的非线性变换,减少过拟合
- 引入平移不变性
- 关注特征而不是它们的位置,降低对位置的敏感性(通过下面两个操作就知道为什么)。卷积操作对位置很敏感。
1.最大池化(Max pooling)
取核对应部分的最大值
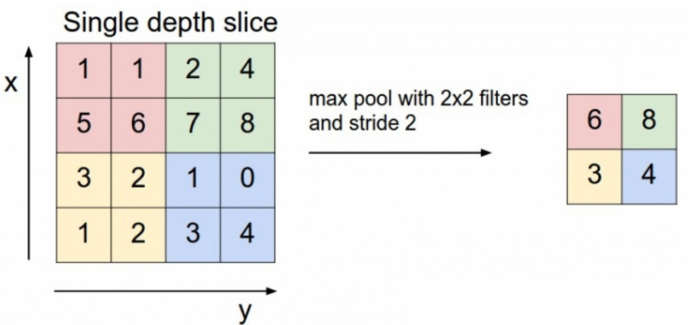
• 达到特征选择的效果
• 引入额外的非线性映射
2.平均池化(Average pooling)
取核对应部分的平均值

• 比起最大池化层更好地保留信息
• 减少神经元数量
• 线性操作
• 全局平均池化可以有效抵抗深度CNN中的过拟合。
全局平均池化(GAP)是一种对整个特征图进行操作的池化方法。它的操作步骤如下:
- 对于给定的特征图,针对每个通道,计算该通道内所有元素的平均值。
- 将每个通道内的平均值作为该通道的汇总特征。
- 最终得到一个包含所有通道汇总特征的向量
- 全局平均池化通常用作最后一层卷积层之后,用来减少特征图的维度,并生成一个包含每个通道重要特征的向量。这个向量可以输入到全连接层或分类器中,以进行最终的分类或预测任务。
最终得到的汇聚特征向量可以看作是整个特征图的全局信息表示
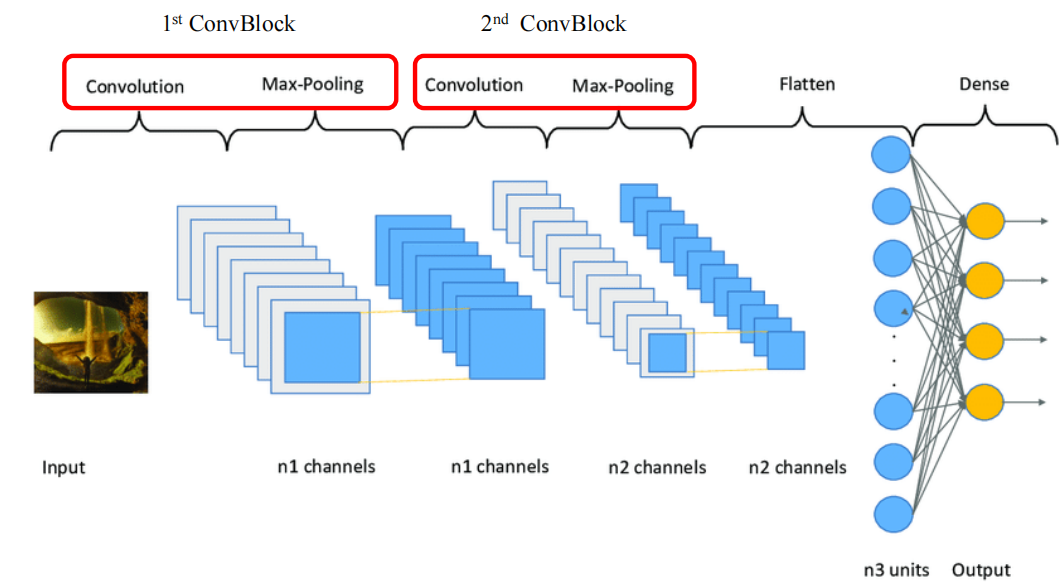
5.卷积块






![[C++]——STL简介](https://img-blog.csdnimg.cn/direct/b1e6fa04f98e41968a2ec3a88b595378.png)