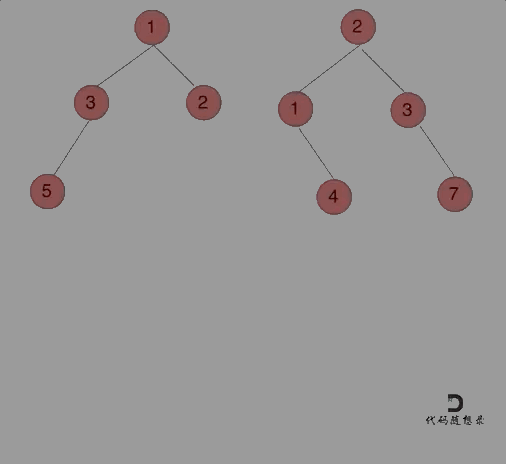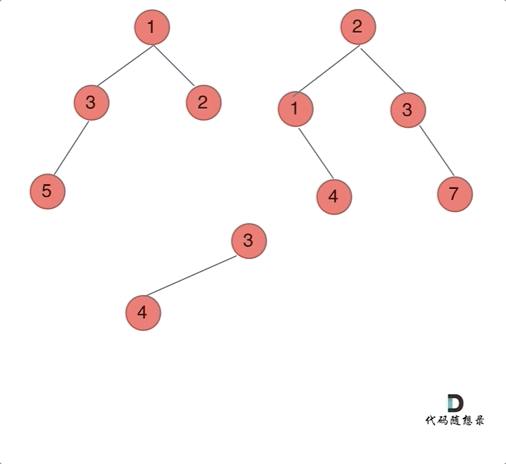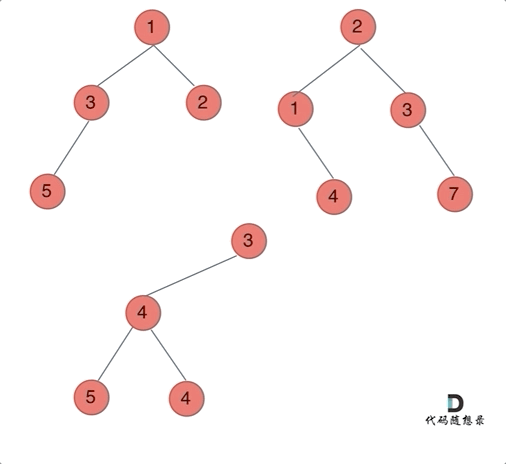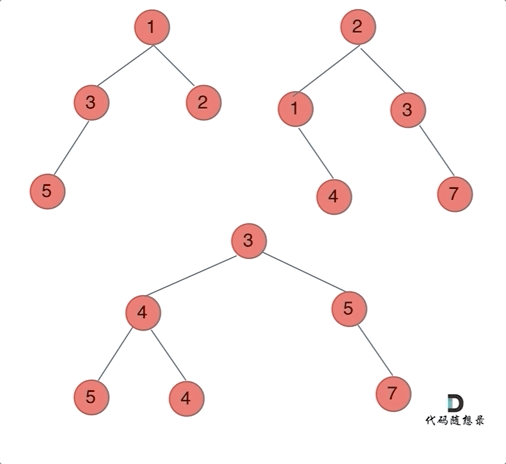
class Solution : def constructMaximumBinaryTree ( self, nums: List[ int ] ) - > Optional[ TreeNode] : if not nums: return max_ = max ( nums) max_index = nums. index( max_) root = TreeNode( max_) root. left = self. constructMaximumBinaryTree( nums[ : max_index] ) root. right = self. constructMaximumBinaryTree( nums[ max_index + 1 : ] ) return rootdef constructMaximumBinaryTree2 ( self, nums: List[ int ] ) - > Optional[ TreeNode] : if len ( nums) == 1 : return TreeNode( nums[ 0 ] ) node = TreeNode( 0 ) max_numb = 0 max_index = 0 for i in range ( len ( nums) ) : if nums[ i] > max_numb: max_index = imax_numb = nums[ i] node. val = max_numbif max_index > 0 : new_list = nums[ : max_index] node. left = self. constructMaximumBinaryTree( new_list) if max_index < len ( nums) - 1 : new_list = nums[ max_index + 1 : ] node. right = self. constructMaximumBinaryTree( new_list) return node
class Solution : def mergeTrees ( self, root1: Optional[ TreeNode] , root2: Optional[ TreeNode] ) - > Optional[ TreeNode] : if not root1: return root2if not root2: return root1node = TreeNode( ) node. val = root1. val + root2. valnode. left = self. mergeTrees( root1. left, root2. left) node. right = self. mergeTrees( root1. right, root2. right) return nodedef mergeTrees1 ( self, root1: Optional[ TreeNode] , root2: Optional[ TreeNode] ) - > Optional[ TreeNode] : if not root1 and not root2: return node = TreeNode( 0 ) if root1 and root2: node. val = root1. val + root2. valnode. left = self. mergeTrees( root1. left, root2. left) node. right = self. mergeTrees( root1. right, root2. right) elif root1 and not root2: node. val = root1. valnode. left = self. mergeTrees( root1. left, None ) node. right = self. mergeTrees( root1. right, None ) else : node. val = root2. valnode. left = self. mergeTrees( None , root2. left) node. right = self. mergeTrees( None , root2. right) return node
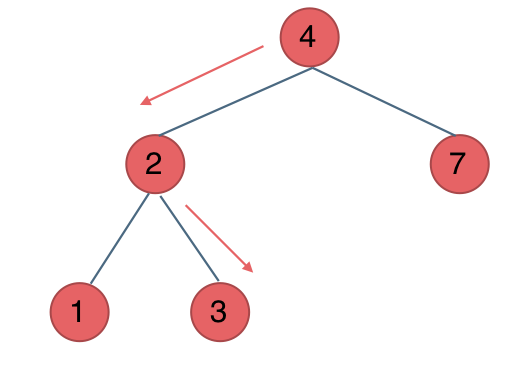
class Solution : def searchBST ( self, root: Optional[ TreeNode] , val: int ) - > Optional[ TreeNode] : queue_1 = [ ] if not root: return None queue_1. append( root) while len ( queue_1) > 0 : node = queue_1. pop( 0 ) if node. val == val: return nodeif node. left: queue_1. append( node. left) if node. right: queue_1. append( node. right) return None def searchBST ( self, root: Optional[ TreeNode] , val: int ) - > Optional[ TreeNode] : while root: if root. val > val: root = root. leftelif root. val < val: root = root. rightelse : return rootreturn None def searchBST ( self, root: TreeNode, val: int ) - > TreeNode: if not root or root. val == val: return rootif root. val > val: return self. searchBST( root. left, val) if root. val < val: return self. searchBST( root. right, val)
class Solution : def __init__ ( self) : self. nums = [ ] def isValidBST ( self, root: Optional[ TreeNode] ) - > bool : self. nums = [ ] self. traversal( root) for i in range ( 1 , len ( self. nums) ) : if self. nums[ i] <= self. nums[ i - 1 ] : return False return True def traversal ( self, root) : if root is None : return self. traversal( root. left) self. nums. append( root. val) self. traversal( root. right)
class Solution : def __init__ ( self) : self. maxVal = float ( '-inf' ) def isValidBST ( self, root) : if root is None : return True left = self. isValidBST( root. left) if self. maxVal < root. val: self. maxVal = root. valelse : return False right = self. isValidBST( root. right) return left and right





![[ CTF ]【天格】战队WriteUp-第七届“强网杯”全国安全挑战赛](https://img-blog.csdnimg.cn/direct/d486ff2244614d0b880b838f14103ead.png#pic_center)