---

最近在做一些机器人位姿优化方面的东西，学习了一下关于智能优化算法方面的内容，于是在这里整理一下。
最近时间比较紧张，就不写太详细了

❤ 2023.12.12 ❤

粒子群算法

参考资料

B站的一个视频，比较简单给了代码
→→→【Matlab 粒子群算法PSO实例学习（有代码和详细注释）】

这个也是B站视频，里面是一个关于matlab优化算法的13讲课程中的一部分，完整版的课程和资料还是很好找的，但是这个课程有点旧，当然里面的算法就更旧了。。。
→→→【我居然只花4个小时就学懂了【优化算法】，遗传算法、蚁群算法、模拟退火算法、粒子群优化算法】

关于粒子群算法参数的调整与改进
→→→【Matlab粒子群算法（PSO）优化程序——调整权重、改进学习因子】

matlab自带的智能算法工具箱的简单介绍
→→→【3-7matlab自带的粒子群工具箱的讲解和演示视频课程】

→→→【】

---

△ matlab工具箱粒子群函数

○ 代码

使用matlab工具箱实现粒子群还是很简单的，但是可以调节的参数有限，不过胜在简单

%% 配置参数
options = optimoptions('particleswarm');
options.SwarmSize = 50;  % 粒子数量
options.MaxIterations = 50;  % 最大迭代次数
options.Display = 'iter';  % 显示每次迭代的信息
% options.UseParallel = true; % 开启并行计算
options.PlotFcn = 'pswplotbestf';nvars = 6;  % 变量的数量
% 变量范围
% x[0.5, 3]
% y[-1.5, 2]
% z[1, 3]?
% A[-180, 180]
% B[-90, 90]
% C[-90, 90]
lb = [0.5,  -2,     1,  -180,   -90,    -90];
ub = [3,     1.5,   3,   180,    90,     90];% 开始计时
tic;[x, fval] = particleswarm( @(x) -1 * objectiveFunction(x), nvars, lb, ub, options);% 结束计时
SolvingTime = toc;fprintf('程序运行时间：%.2f 秒。\n', SolvingTime);disp("最优解: " + mat2str(x));
disp("目标函数值: " + num2str(-fval));%% 
function y = objectiveFunction(x)Pose_workpiece = [x(1) x(2) x(3) x(4) x(5) x(6)];y = Get_Comprehensive_Stability_Coefficient_PSO(Pose_workpiece);
end

需要注意的是函数默认寻找的是最小值，如果想找的是最大值需要手动加个负号

另外据chatgpt说也可以实时监测求解过程的情况，但是他给的代码一直报错我就放弃了。。。

---

○

○ 手搓代码实现粒子群优化 2个变量（xy）的粒子群优化尝试

我的代码基于

→→→【Matlab 粒子群算法PSO实例学习（有代码和详细注释）】

感谢up~

· 定义函数

Pose_workpiece = [x(1) x(2) 1.3 0 -45 0];

因为更改了原点位置，所以曲面图有变化

surf：

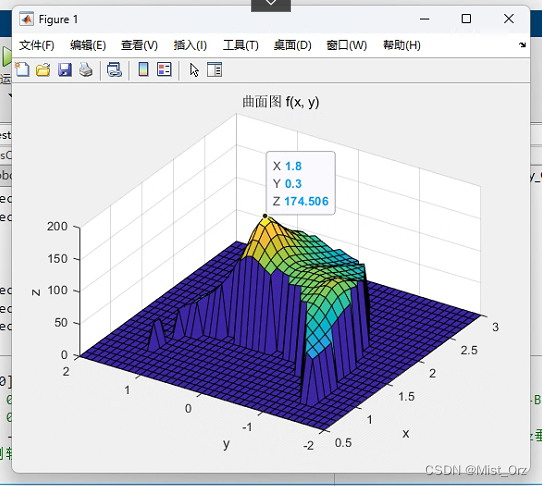
mesh：

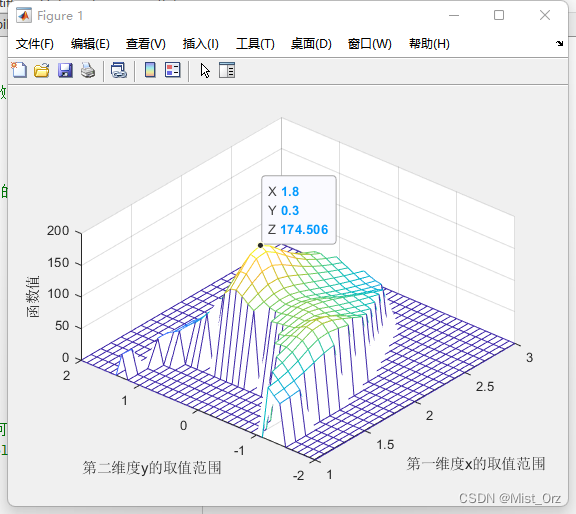
% xy优化
function y = objectiveFunction(x)%     Pose_workpiece = [x(1) x(2) x(3) x(4) x(5) x(6)];Pose_workpiece = [x(1) x(2) 1.3 0 -45 0];y = Get_Comprehensive_Stability_Coefficient_PSO(Pose_workpiece);
end

---

· 绘制网格图（用来可视化过程）

%% 调用函数绘制网格
f = @(x) objectiveFunction(x);
figure(1);
[X, Y] = meshgrid(1:0.1:3, -2:0.1:2);  % 生成网格数据
x = [X(:), Y(:)];% 对 x 中的每一行应用函数 f
% y0 = arrayfun(@(i) f(x(i, :)), 1:size(x, 1));
y0 = load('y0_for_test_mesh_data.mat'); % 将计算好的网格数据读入
y0 = y0.y0;% 重塑 y0 以匹配 X 和 Y 的尺寸
y0_matrix = reshape(y0, size(X));% 计算梯度
[Cx, Cy] = gradient(y0_matrix, 0.1, 0.1);% 绘制网格图
mesh(X, Y, y0_matrix);%  colorbar;%可以看到色板，也可以给指定区域指定颜色%set(h,'EdgeColor','b','FaceColor','w','MarkerEdgecolor','r','MarkerFacecolor','y')
xlabel('第一维度x的取值范围');
ylabel('第二维度y的取值范围');
zlabel('函数值');
hold on;

就是上面那个效果

---

· 参数初始化，绘制粒子初始位置

%% 开始种群等基本定义
N = 50;                           % 初始种群个数
d = 2;                             % 空间维数（参看上述的函数表达式）
ger = 50;                         % 最大迭代次数     
plimit = [1,3;-2,2];              % 设置位置参数限制(矩阵的形式可以多维)，现在2X2矩阵
vlimit = [-0.5, 0.5;-0.5, 0.5];    % 设置速度限制【？】
w = 0.8;                           % 惯性权重,个体历史成绩对现在的影响0.5~1之间【？】
%还有自适应调整权重、随机权重等等
%（不同的权重设置很影响性能，按需要选取）c1 = 0.5;                          % 自我学习因子【？】
c2 = 0.5;                          % 群体学习因子 【？】tic;                              %计时开始for i = 1:dx(:,i) = plimit(i, 1) + (plimit(i, 2) - plimit(i, 1)) * rand(N, 1);%初始种群的位置end                              %rand(N,1)产生N行一列范围在1之内的随机数%第一列,第二列：x=0+（20-0）*（1之内的随机数）                                    v = rand(N, d);                   % 初始种群的速度,500行2列分别在两个维度上
xm = x;                           % 每个个体的历史最佳位置
ym = zeros(1, d);                 % 种群的历史最佳位置，两个维度，设置为0
fxm = zeros(N, 1);                % 每个个体的历史最佳适应度，设置为0
fym = -inf;                       % 种群历史最佳适应度,求最大值先设置成负无穷n = size(x, 1);
fx_plot = zeros(n, 1);  % 初始化结果数组
parfor i = 1:nfx_plot(i) = f(x(i, :));
endplot3(xm(:,1),xm(:,2),fx_plot, 'mo');   %r红,g绿,b蓝,c蓝绿,m紫红,y黄,k黑,w白
title('种群初始分布状态图');        %plot3在三维区域画出空间上的点，把格式设置成‘o’用来画每个位置的散点图
hold on;  %figure(2);
%mesh(x0_1, x0_2, y0);
%hold on;
%plot3(xm(:,1),xm(:,2),f(xm(:,1),xm(:,2)), 'ro');
%hold on;iter=1;                             %初始的迭代次数因为用while设置为一times = 1; 
record = zeros(ger, 1);             %记录器

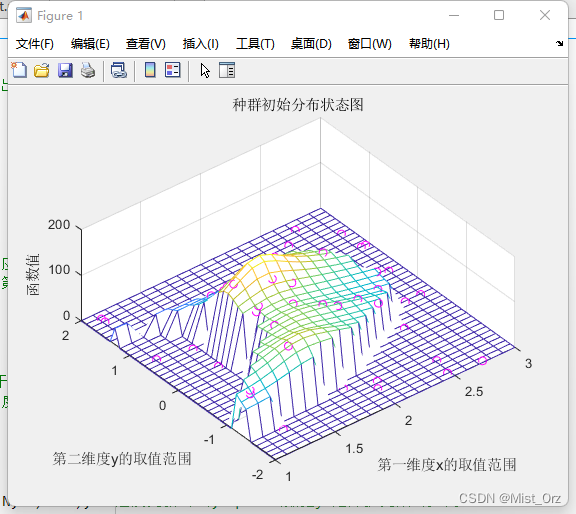
还挺好看。。。

---

· 开始迭代过程并绘图

%% 迭代更新开始
while iter <= ger
%      fx = f(x(:,1),x(:,2));         % 代入x中的二维数据，算出个体当前适应度,为500行1列的数据   n = size(x, 1);fx = zeros(n, 1);  % 初始化结果数组parfor i = 1:nfx(i) = f(x(i, :));endfor i = 1:N                    %对每一个个体做判断if fxm(i) < fx(i)           %如果每个个体的历史最佳适应度小于个体当前适应度fxm(i) = fx(i);         % 更新个体历史最佳适应度,第一轮就是把小于零的清除xm(i,:) = x(i,:);       % 更新个体历史最佳位置end endif fym < max(fxm)                  %种群历史最佳适应度小于个体里面最佳适应度的最大值[fym, nmax] = max(fxm);    % 更新群体历史最佳适应度,取出最大适应度的值和所在行数即位置ym = xm(nmax, :);          % 更新群体历史最佳位置end% 速度更新v = v * w + c1 * rand *(xm - x) + c2 * rand *(repmat(ym, N, 1) - x); % 速度更新公式,repmat函数把ym矩阵扩充成N行1列% 边界速度处理for i=1:d for j=1:Nif  v(j,i)>vlimit(i,2)      %如果速度大于边界速度，则把速度拉回边界v(j,i)=vlimit(i,2);endif  v(j,i) < vlimit(i,1)     %如果速度小于边界速度，则把速度拉回边界v(j,i)=vlimit(i,1);endendend      % 位置更新x = x + v; % 位置更新for i=1:d for j=1:Nif  x(j,i)>plimit(i,2)x(j,i)=plimit(i,2);endif  x(j,i) < plimit(i,1)x(j,i)=plimit(i,1);endendendrecord(iter) = fym;            %记录最大值if times >= 2cla;                    %清除轴线图形mesh(X, Y, y0_matrix);% 并行计算优化n = size(x, 1);fx_plot = zeros(n, 1);  % 初始化结果数组parfor i = 1:nfx_plot(i) = f(x(i, :));endplot3(x(:,1),x(:,2),fx_plot, 'ro');title('状态位置变化');pause(0.5);times=0;enditer = iter+1;times=times+1;
end

---

· 获取结果并绘图

%% 作图
figure(3);
plot(record);                %画出最大值的变化过程
title('收敛过程');figure(4);
mesh(X, Y, y0_matrix);
hold on;% 并行计算优化
n = size(x, 1);
fx_plot = zeros(n, 1);  % 初始化结果数组
parfor i = 1:nfx_plot(i) = f(x(i, :));
endplot3(x(:,1),x(:,2),fx_plot, 'ro');title('最终状态图');disp(['最大值为：',num2str(fym)]);
disp(['最大值点位置：',num2str(ym)]);
toc;    %计时结束

---

· 运行结果

设置种群数量10，迭代次数10，验证程序流程

符合预期

---

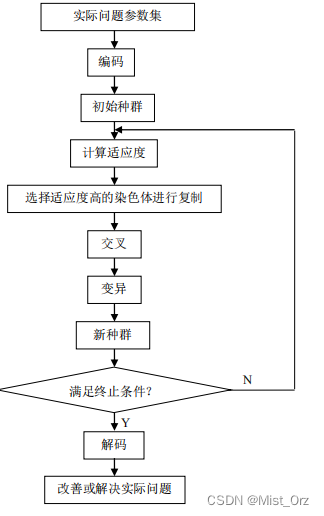
遗传算法

△ 遗传算法概念