一、核心步骤
1.准备容器
准备一个盒子div。
2.引包
从官网引包，有开发版本和生产版本之分。
3.创建Vue实例
创建一个Vue实例，new Vue()。
4.指定配置项
指定配置项，用于渲染数据 。
el：指定挂载点。知道自己将来要管理的是哪一个容器/盒子。
data：提供数据。容器里变量的具体数据从 data 这里获取。
二、实操
1.打开VSCode
（1）新建一个.html文件。
（2） 英文键按 ! 加 Tab 键/Enter键，快速生成 html 基本结构骨架
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>Document</title>
</head>
<body></body>
</html>2.准备容器 div
3.引包（从官网）
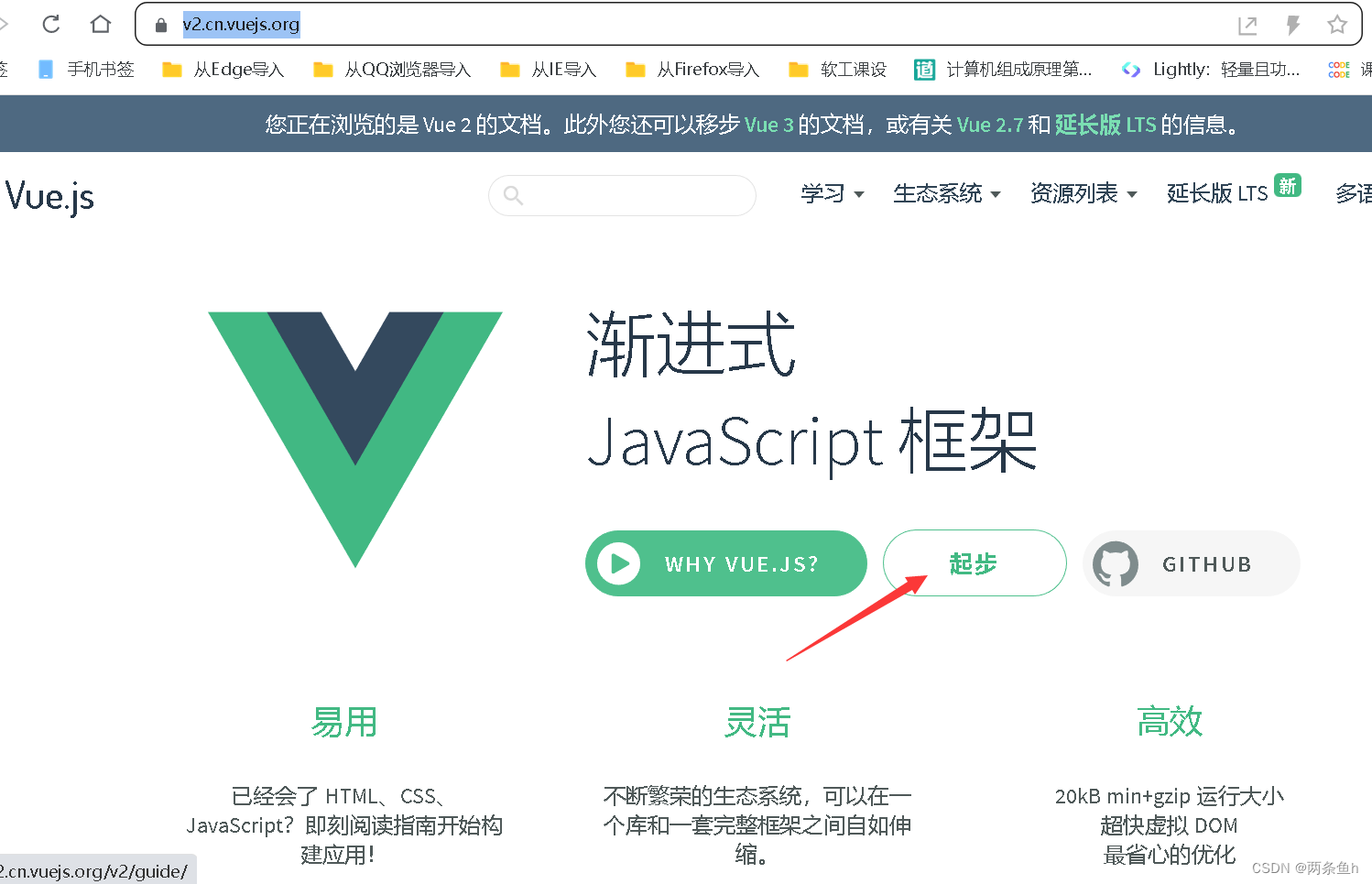
浏览器地址栏输入：v2.cn.vuejs.org ,回车进入 Vue2 官网。
起步→安装→往下滑到#CDN→复制第一个代码（在线使用，也可以往上滑一个内容下载安装直接引入script使用。笔者这里学习就使用在线方式引包）
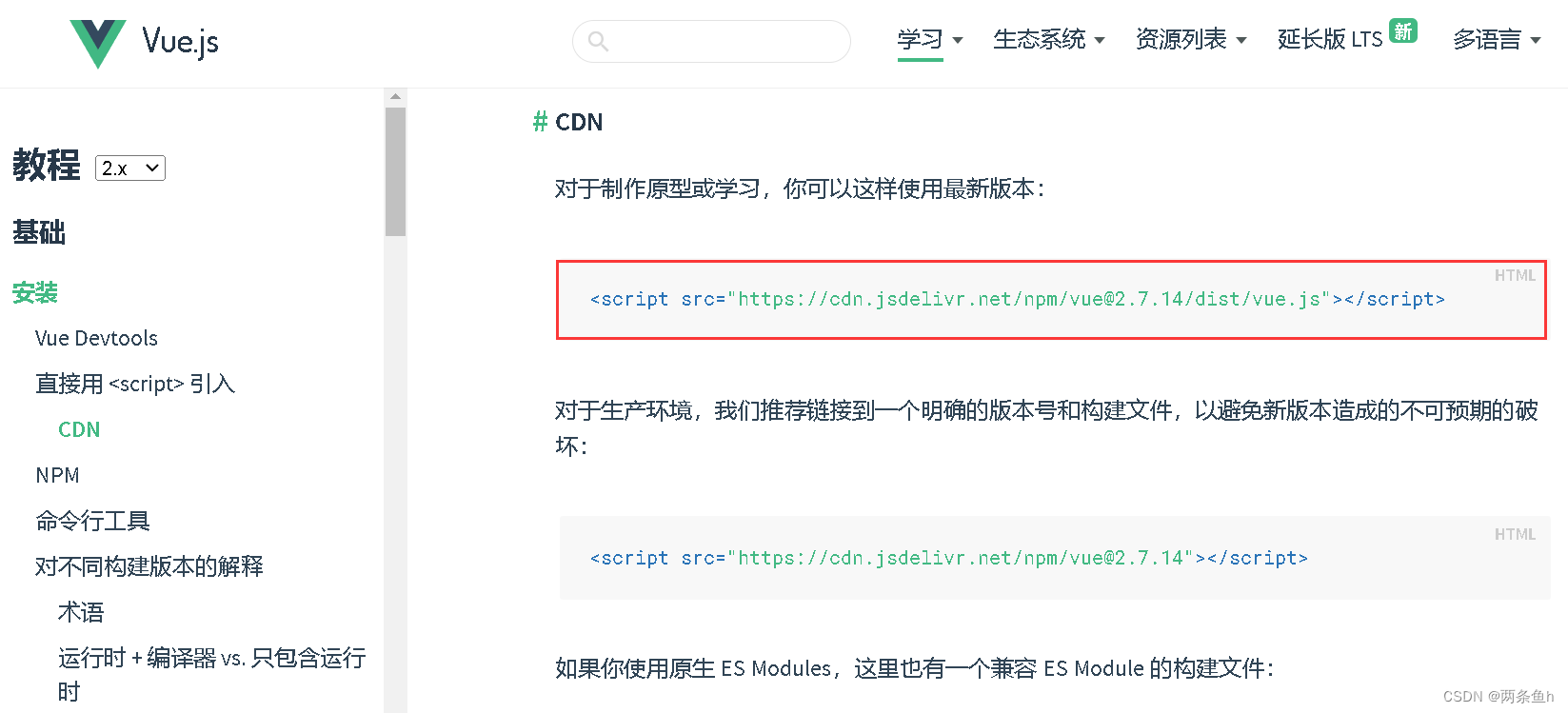将复制的代码粘贴到 div 标签后面。
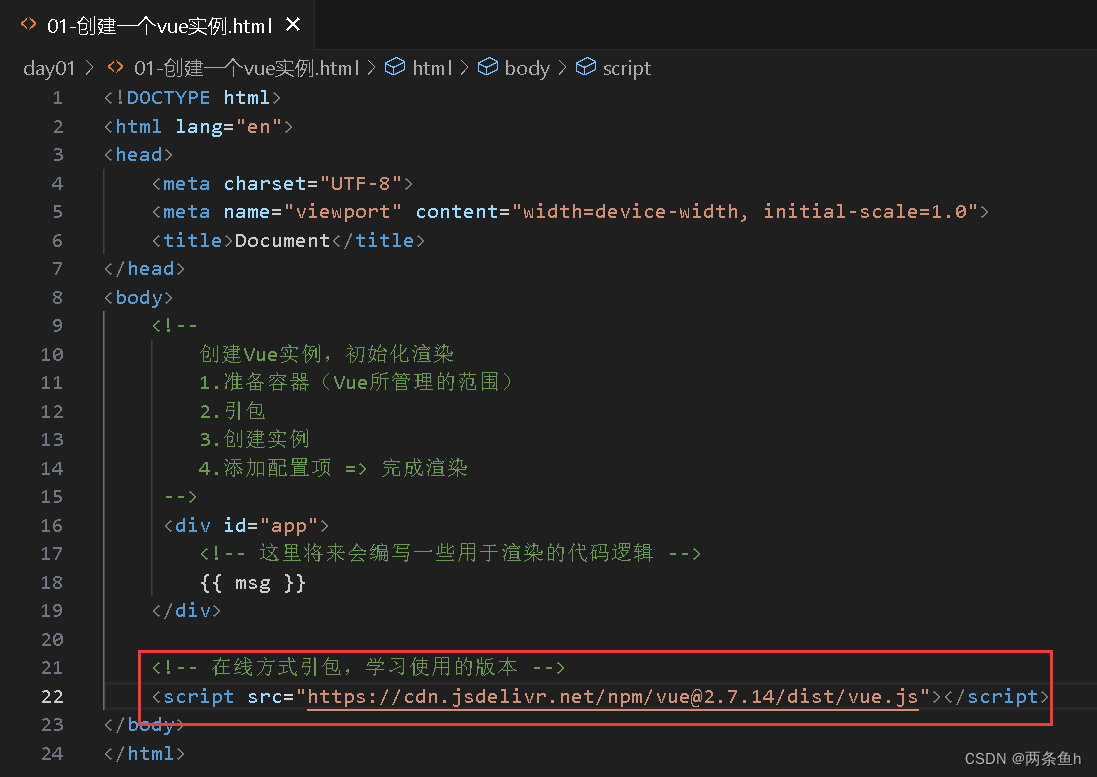
4.创建实例 new Vue（）
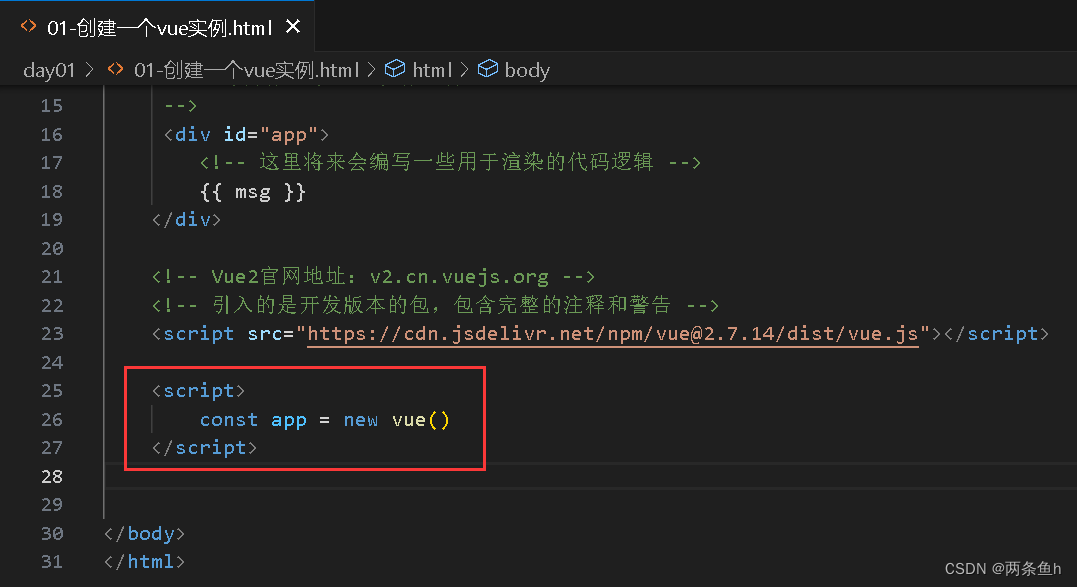5.指定配置项
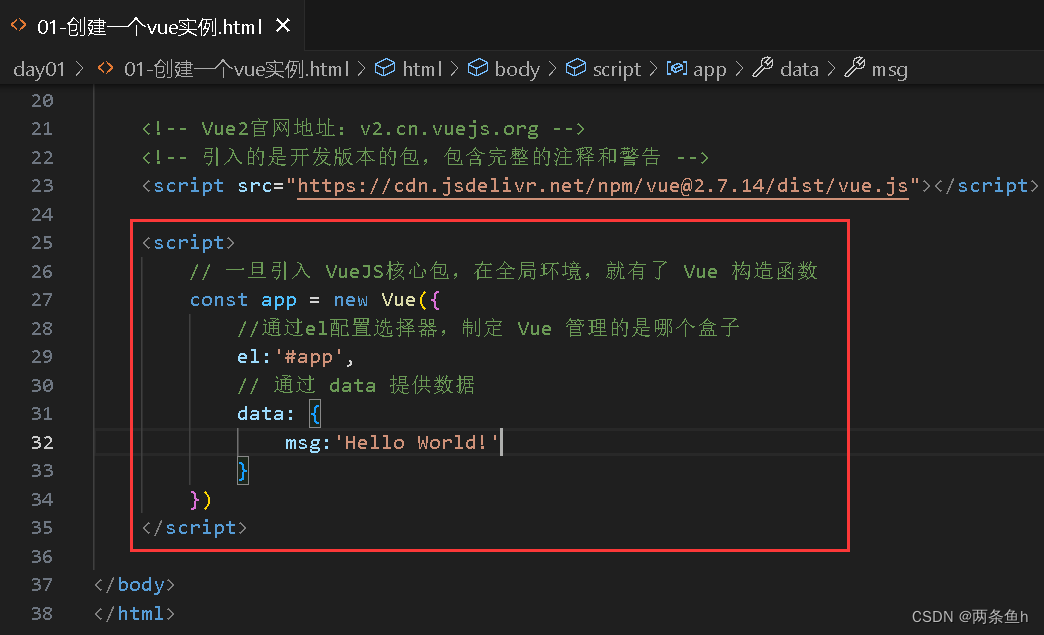6.Alt+B打开浏览器查看效果
需要事先安装打开浏览器的插件，没安装的先安装：VSCode下载安装教程+安装插件_vscode下载中文插件-CSDN博客
安装好插件后，Alt+B打开浏览器查看效果：
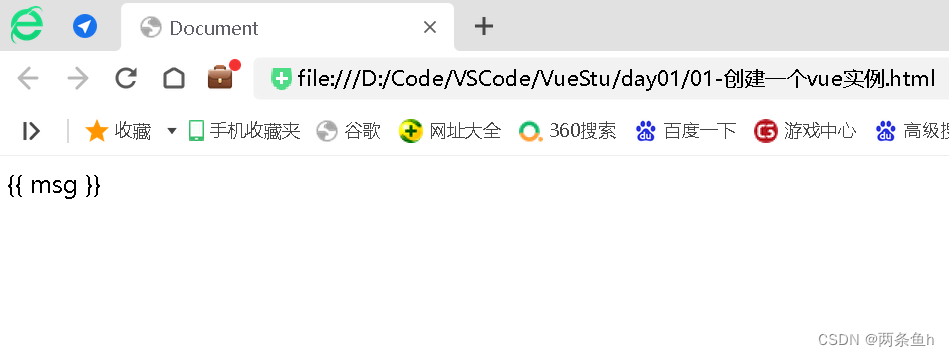
然而有些小伙伴可能会发现，浏览器没有跟代码同步，没有显示“Hello World!”，这里用的是360浏览器。
所以通过实例告诉大家，学习的时候建议使用谷歌浏览器，就不会有这种问题。
也可以通过安装live server插件的方式解决，这个插件是一个具有实时加载功能的小型服务器。
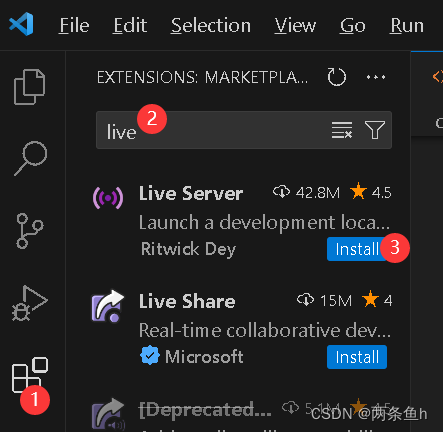
出现以下界面即安装成功：
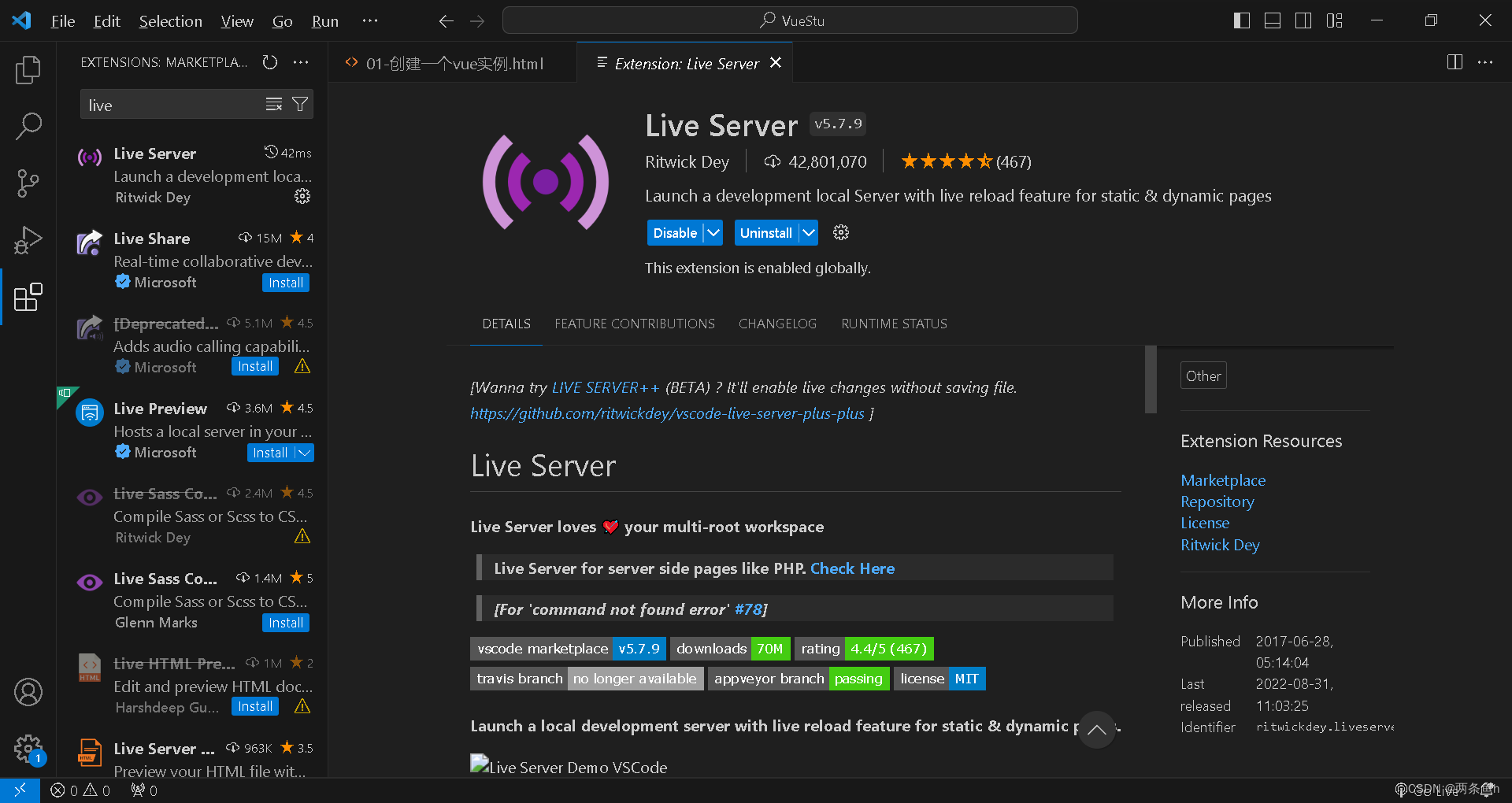
后续还需要对这个插件进行一些配置，笔者不太懂这个配置，有需要的小伙伴可以自己去搜一下 ，或者直接看这篇写的挺不错的。
最后附上完整代码：
<!DOCTYPE html>
<html lang="en">
<head><meta charset="UTF-8"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>Document</title>
</head>
<body><!-- 创建Vue实例，初始化渲染1.准备容器（Vue所管理的范围）2.引包3.创建实例4.添加配置项 => 完成渲染--><div id="app"><!-- 这里将来会编写一些用于渲染的代码逻辑 -->{{ msg }}</div><!-- Vue2官网地址：v2.cn.vuejs.org --><!-- 引入的是开发版本的包，包含完整的注释和警告 --><script src="https://cdn.jsdelivr.net/npm/vue@2.7.14/dist/vue.js"></script><script>// 一旦引入 VueJS核心包，在全局环境，就有了 Vue 构造函数const app = new Vue({//通过el配置选择器，制定 Vue 管理的是哪个盒子el:'#app',// 通过 data 提供数据data: {msg:'Hello World!'}})</script></body>
</html>至此就完成创建一个Vue实例了，若有错处欢迎评论区留言指正。
