1.input(1:m,:)‘含义

矩阵A第一列的转置矩阵。(x,y)表示二维矩阵第x行第y列位置的元素，x为:则表示所有的行。因此，A(:,1)就表示A的第1列的所有元素，这是一个列向量。

所以这里input(1:m,:)表示1到m行，所有列，而后面有个'这代表转置，综合来看就是将一个1到m行，所有列的矩阵进行转置。

2.如何在workspace中导入数据

首先点击左上角的import data

选择要导入的文件即可，之后会弹出新的界面，界面如下：

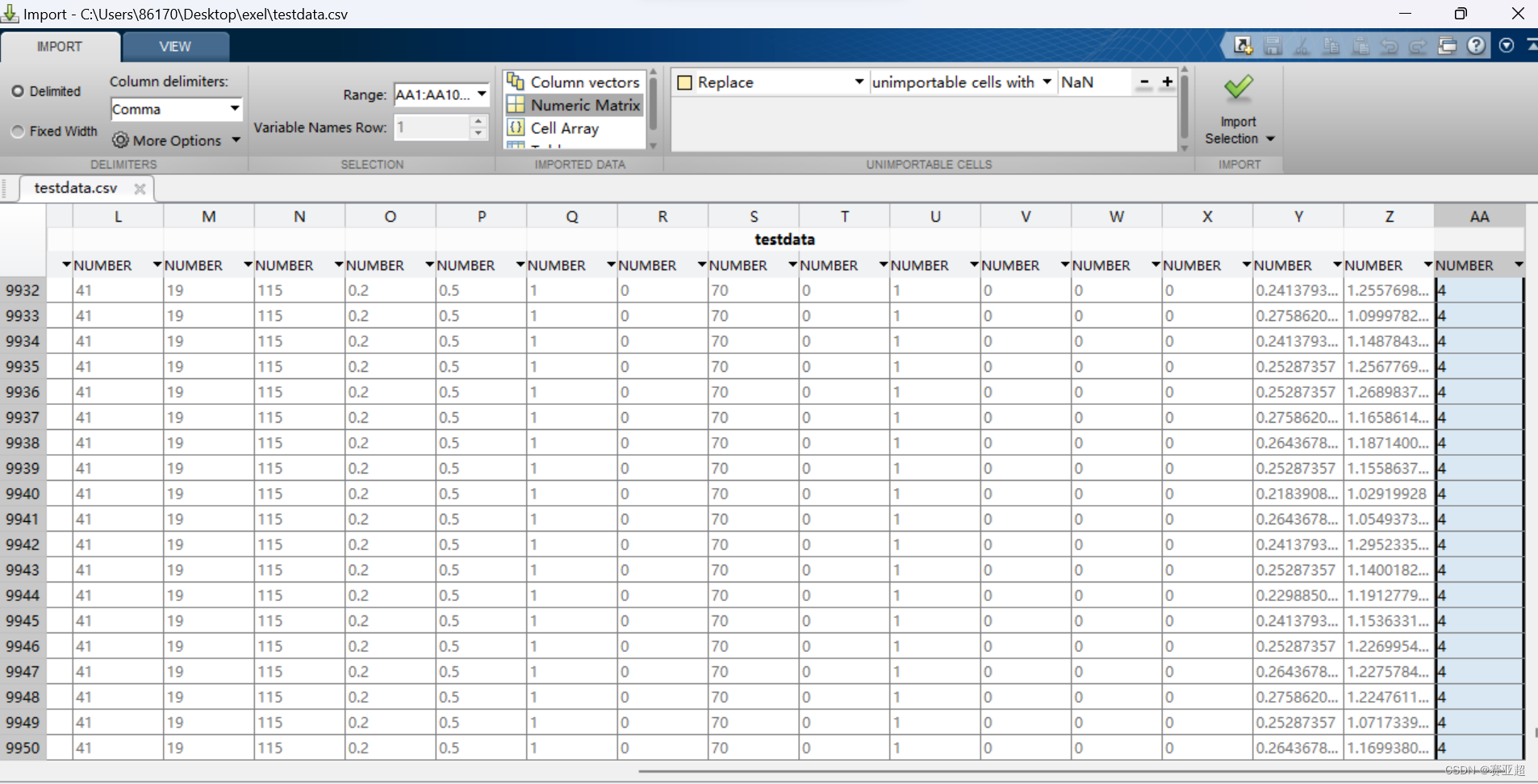
这里用到的地方就是range（范围）以及matrix（矩阵），range选择自己想要的的行与列即可。

之后点击对勾就可以导入到workspace里面。

3.newff函数

参考文章：

Matlab中newff函数使用方法和搭建BP神经网络的方法-CSDN博客

net = newff(data,label,[8,8],{'tansig','purelin'},'trainlm')

data：训练时网络的输入数据。newff函数会把data的一列当作一个样本，如果你的数据集是一行当作一个样本，记得将你的输入数据矩阵转置data.‘
label：对应输入数据的标签，也可以看作真实输出。同上，newff函数会把label的一列当作一个样本的标签，如果你的数据集是一行当作一个样本，记得将你的输入数据矩阵转置label.‘
[8,8]：用于确定神经网络隐藏层的层数以及每层的神经单元个数。[8,8]就表示该网络包含两个隐藏层，每个隐藏层有8个神经单元
{‘tansig’,‘purelin’}：表示个隐藏层所用的激活函数。{‘tansig’,‘purelin’}表示第一层用tansig激活函数，是一种S型激活函数；第二次用purelin激活函数，是一种线性型激活函数。常见的激活函数如下：

 logsig：对数S型函数tansig：正切S型函数purelin：线性型函数

‘trainlm’：确定训练函数，默认为trainlm函数，该方法需要占用更大的存储空间，使用了Levenberg-Marquardt算法,对于中等规模的BP神经网络有最快的收敛速度。由于其避免了直接计算赫赛矩阵,从而减少了训练中的计算量,但需要较大内存量，随着神经元的增多，训练时间增加较大。常见的训练方法如下：
 

 traingd：梯度下降算法traingdm：带动量的梯度下降算法traingda：学习率变化的梯度下降算法traingdx：学习率变化带动量的梯度下降算法trainrp：RPROP算法，内存需求小，适用于大型网络trainoss：OneStep Secant Algorithm，计算量与内存需求较小，适用于大型网络

（2）其他参数设置：
net.trainParam.goal = 1e-3 ：确定目标值为0.001，到此值时训练停止
net.trainFcn=‘trainlm’ ：确定训练函数trainlm。如果newff（）中设置了，后续可以用不设置
net.trainParam.lr = 0.1 ： 确定学习率为0.1
net.divideFcn = ‘’ ：取消newff（）默认再次划分操作。newff（）默认将训练集重新划分6：2：2，训练集：测试集：验证集，在训练过程中会自动在某一处停止，我认为是为了防止过拟合吧，实践中在新训练集损失和新验证集损失下降不明显，且验证损失有上升的趋势时停止。对于数据本来就少的情况，建议取消划分。
net.trainParam.epochs = 1000 ：训练最大迭代次数
net.trainParam.min_grad =1e-24 ： 最小梯度值，到此值时训练停止
4.net.iw与net.b的含义

MATLAB中多层网络的net.lw{i,j}和net.b{k}的含义 - 知乎 (zhihu.com)

先假设神经网络结构，{ 9 [80 50 20] 1 }；9为输入层，[80 50 20]为隐层，1为输出层。

1. net.iw{1,1} 表示 输入层 到 第1层隐层 的权重，为80*9的矩阵；
2. net.lw{2,1} 表示 第1层隐层 到 第2层隐层 的权重，为50*80的矩阵；
3. net.lw{3,2} 表示 第2层隐层 到 第3层隐层 的权重，为20*50的矩阵；
4. net.lw{4,3} 表示 第3层隐层 到 输出层 的权重，为1*20的矩阵；
5. net.b{1} 表示 第1层隐层 的偏置，为80*1的矩阵；
6. net.b{2} 表示 第2层隐层 的偏置，为50*1的矩阵；
7. net.b{3} 表示 第3层隐层 的偏置，为20*1的矩阵；
8. net.b{4} 表示 输出层 的偏置，为1*1的矩阵；

可以以此类推。

所以net.iw{1,1}，模式也是固定的，仅表示输入层到第1层隐层的权重，之后就net.lw的事情了。net.lw{i,j} 表示 第j层隐层 到 第i层隐层 的权重。net.b{k} 表示 第k层隐层 的偏置或者说阈值，结构都为列向量。可以看出，这里假设的隐含层只有3层[80 50 20]，但net中将最后一层输出层也当隐含层用了，所以 i 和 k 可以取到4。

知道权重和偏置的位置，可以用算法优化，如遗传算法等。

5.validation checks功能

matlab神经网络使用说明及validation check的作用_matlab中的validation-CSDN博客

当创建神经网络进行训练时，原始数据被自动分成training set、validation set 及test set 三部分。

training set：训练样本数据
validation set：验证样本数据
test set：测试样本数据

这三个数据集是没有重叠的，默认比例为7:1.5:1.5

可以通过设置改变比例分配：

net.divideParam.trainRatio = 80/100;
net.divideParam.valRatio = 0/100;
net.divideParam.testRatio = 20/100;

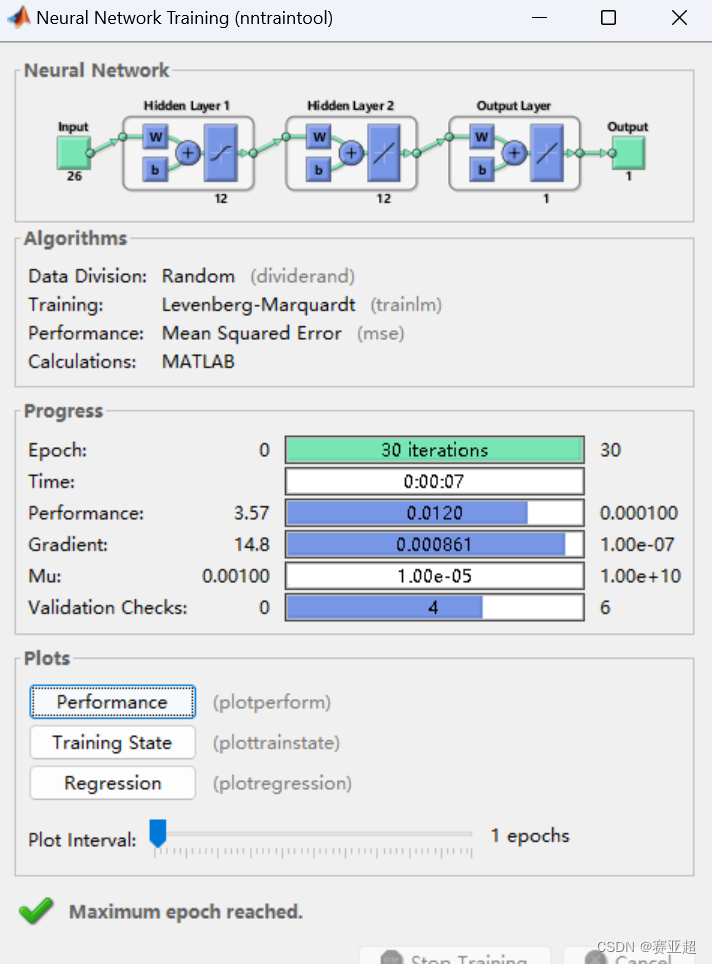
Neural Network

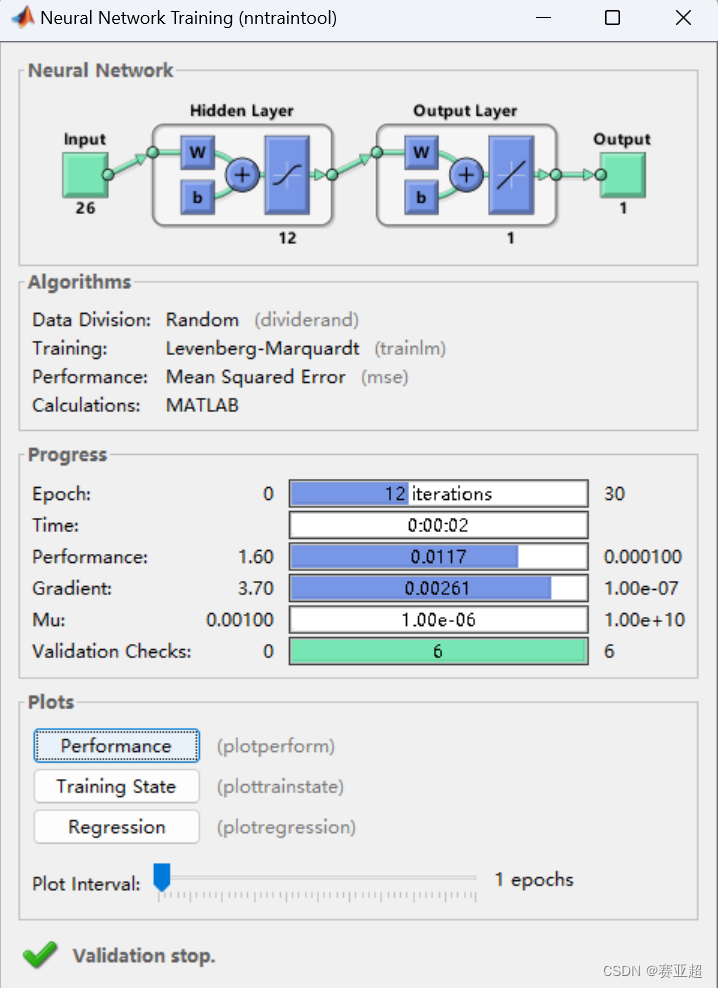
该部分展示了神经网络的结构，从结构图中可以看出该网络有三个隐含层，神经元个数分别为9个、8个、7个

Progress
Epoch：该网络允许的迭代次数最大为1000，实际迭代5次

Time：该网络训练时长为3秒

Performance：该网络的最大误差为0.475，目标误差为0.001，实际误差为0.000520，可在Plots中的Performance中详细查看

Gradient：该网络的最大梯度为1.91，阈值梯度为1 * e -7 ，实际梯度为0.033。可在Plots中的Training State中详细查看

Mu：该网络所使用Levenberg–Marquardt算法中的阻尼因子最小值为0.001，阈值为1* e 10 ，实际值为1* e -6 ，Mu值越大意味着算法收敛效果越好。可在Plots中的Training State中详细查看

Validation Checks：该网络的泛化能力检查标准，实际值为0表示在训练过程中误差在持续降低，若连续6次训练误差无法降低，则结束训练任务。可在Plots中的Training State中详细查看

Plots
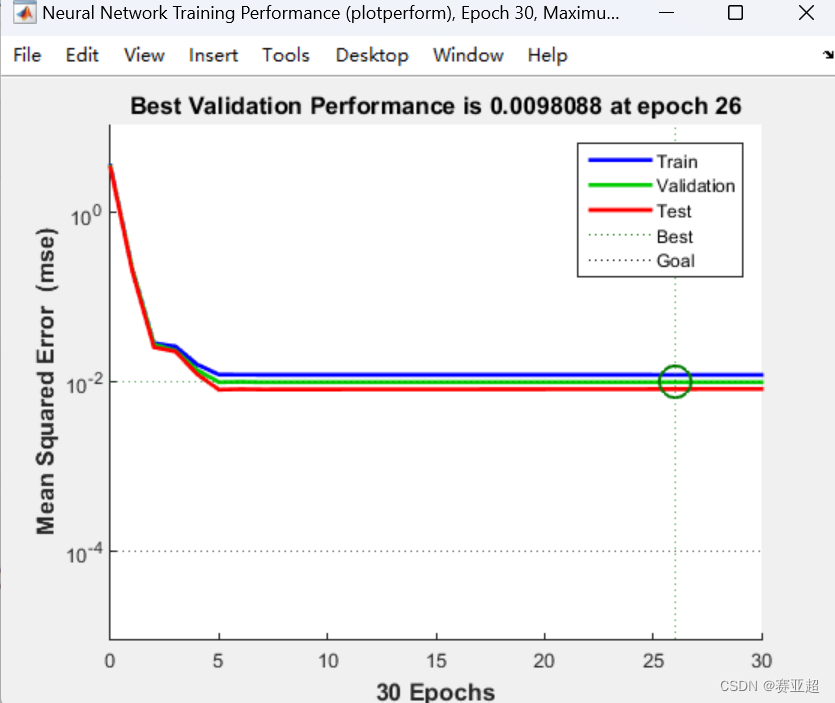
Performance：该网络训练过程中的误差变换可视化

Training State：该网络训练过程中的梯度、Mu因子和泛化能力变换等信息的可视化

Regression：该网络训练集、验证集、测试集的回归能力可视化

Plot Interval：图中横坐标的刻度

matlab神经网络中的validation check
验证样本的检查值默认是6，是指在网络利用训练样本进行训练的过程中，验证样本的误差连续6次迭代不再下降，则训练终止（这只是训练终止条件之一，其他的如训练步数，目标误差等，满足任一条件，训练过程都将终止）。

我们可以这样理解，如果随着网络的训练，验证样本的误差已经基本不再减小，甚至增大，那么就没有必要再去训练网络了。因为即使继续训练下去，当我们利用测试样本进行网络测试时，测试样本的误差同样也不会有所改善，甚至会过度拟合。validation checks已经达到设置的值了，所以网络停止训练，即如果网络在连续max_fail epochs后不能提高网络性能，就停止训练。

通常，有三种方法解决这个问题：

提高validation checks的数值，比如设置net.trainParam.max_fail = 200，其实，这就是自己糊弄自己，非常不严谨，严重不推荐。训练时候，出现停止这种情况，就是因为被训练的网络出现了问题，已经过拟合，应该停下来。但6，的确，可能，有点小，建议改为10到20之间的数吧？这个需要细细思量一下，一般情况默认就好吧？

修改被训练的网络，比如说再加一个隐藏层试试

如果是数据太相近的问题，试试选择用输入训练数据的乱序排法，以及分类

我们要明白它为什么要停止。连续6次误差不断增大，说明网络性能越训练越差。这可能是两方面原因：

过拟合。网络学习得太好了，反而泛化能力下降。

网络规模不够大，信息存储能力不够强，原先学习的知识又被新样本抹去了，导致网络性能无法提升。

要解决这个问题：

如果要改变validation的验证次数，可以用这个语句net.trainParam.max_fail = 20;

或者是增多隐节点或隐层数。

另外，提前停止的网络虽然陷入局优，但不一定就不能用吧，看一下实际效果；

一般来说，不下降就是增大，不可能误差不变。数据少就降低隐层节点数。

取消validation check

加入如下参数，可以取消validation check功能

net.divideFcn =''

但是这个方法对于网络的训练精度提高和输出的逼近程度没有显著改善

matlab神经网络训练过程
在训练时，用training训练，每训练一次，系统自动会将validation set中的样本数据输入神经网络进行验证，在validation set输入后会得出一个误差（不是网络的训练误差，而是验证样本数据输入后得到的输出误差，可能是均方误差），而此前对validation set会设置一个步数，比如默认是6echo，则系统判断这个误差是否在连续6次检验后不下降，如果不下降或者甚至上升，说明training set训练的误差已经不再减小，没有更好的效果了，这时再训练就没必要了，就停止训练，不然可能陷入过学习。所以validation set有个设置步数，就是起这个作用。
复现代码如下:

close all
clc
%读取数据
input=X;
output=Y;
%设置训练数据与测试数据
input_train=input(1:8000,:)';
output_train=output(1:8000,:)';
input_test=input(8001:10000,:)';
output_test=output(8001:10000,:)';
%节点个数
inputnum=26;%输入层节点数量
hiddennum=12;%隐藏层节点数量
outputnum=1;%输出层节点数量
%训练数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);
%bp神经网络
net=newff(inputn,outputn,hiddennum,{'tansig','purelin'},'trainlm');
W1=net.iw{1,1};
B1=net.b{1};
W2=net.lw{2,1};
B2=net.b{2};
%网络参数配置
net.trainParam.epochs=30;
net.trainParam.lr=0.001;
net.trainParam.goal=0.0001;
%网络训练
net=train(net,inputn,outputn);
%测试样本归一化
inputn_test=mapminmax('apply',input_test,inputps);
%神经网络预测
an=sim(net,inputn_test);
%预测结果反归一化与预测值误差计算
test_simu=mapminmax('reverse',an,outputps);
error=test_simu-output_test;
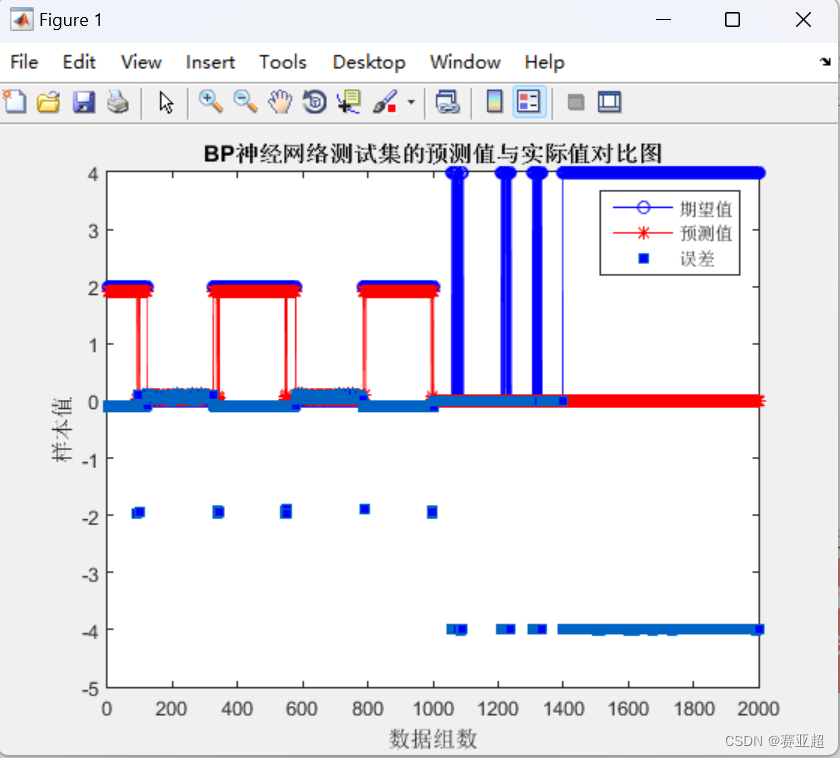
%%第十步 真实值与预测值误差比较plot(output_test,'bo-')
hold on
plot(test_simu,'r*-')
hold on
plot(error,'square','MarkerFaceColor','b')
legend('期望值','预测值','误差')
xlabel('数据组数')
ylabel('样本值')
title('BP神经网络测试集的预测值与实际值对比图')[c,l]=size(output_test);
MAE1=sum(abs(error))/l;
MSE1=error*error'/l;
RMSE1=MSE1^(1/2);disp(['隐含层节点数为',num2str(hiddennum),'时的误差结果如下：'])
disp(['平均绝对误差MAE为：',num2str(MAE1)])
disp(['均方误差MSE为：       ',num2str(MSE1)])
disp(['均方根误差RMSE为：  ',num2str(RMSE1)])
predict_y = zeros(10000,1); % 初始化predict_y
pre_test=mapminmax('apply',new_X(:,:)',inputps);% 对预测数据进行归一化
for i = 1: 10000result = sim(net, pre_test(:,i));predict_y(i) = result;
end
disp('预测值为：')
predict_y=mapminmax('reverse',predict_y,outputps); %把预测结果还原
disp(predict_y)

目前训练过程中有问题，总是训练不完迭代次数就结束。

效果如下：

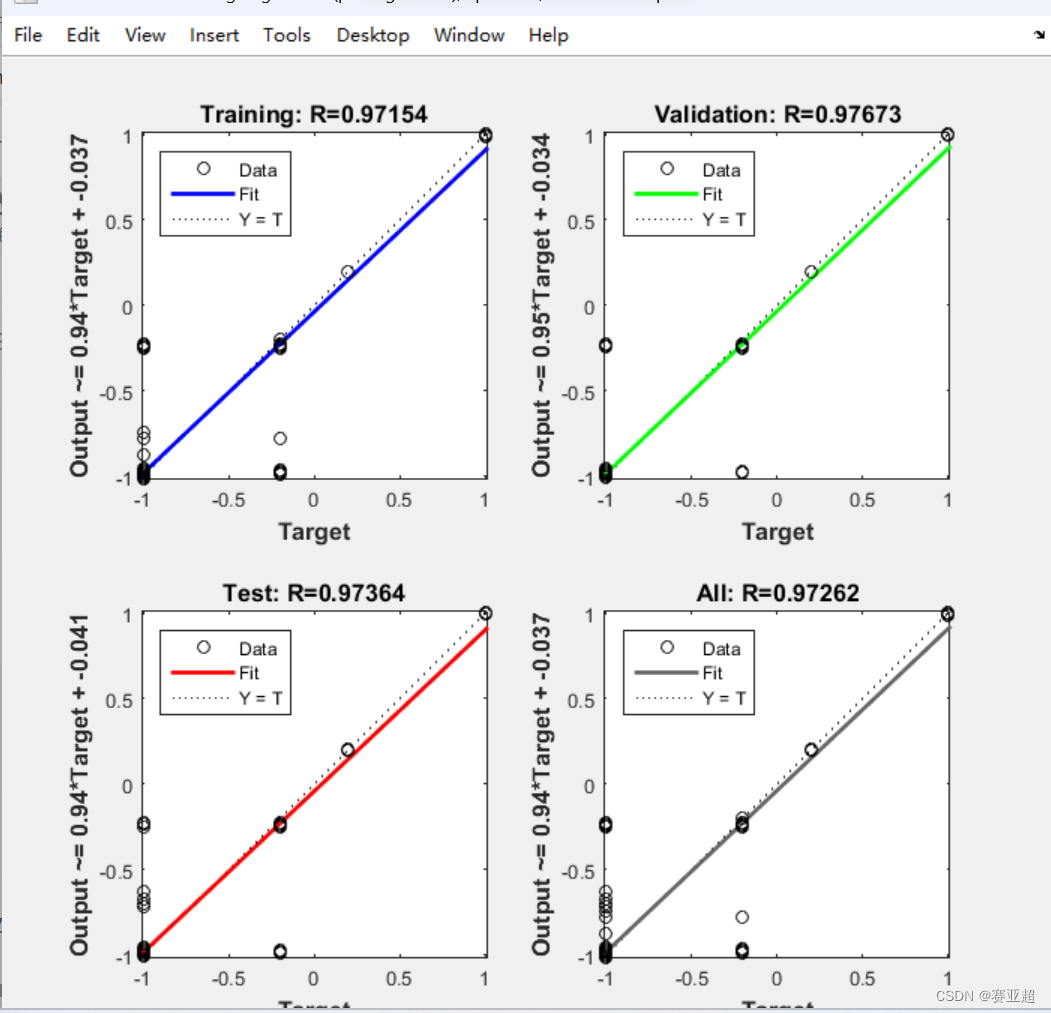
上面是预测结果；

5.解决方法

（1）通过增加隐藏层数，可以看到训练能够训练完，但是平均绝对误差并没有多大变化。但是我发现得出的结果预测值精度变高了，这与增加了一层有关。

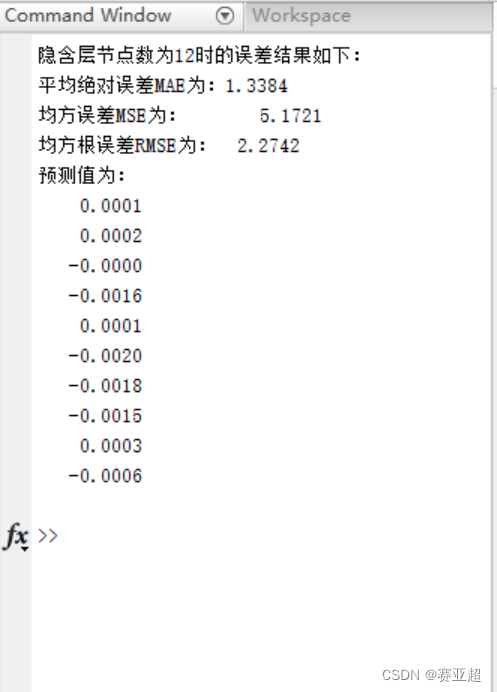
下面是数据分析：

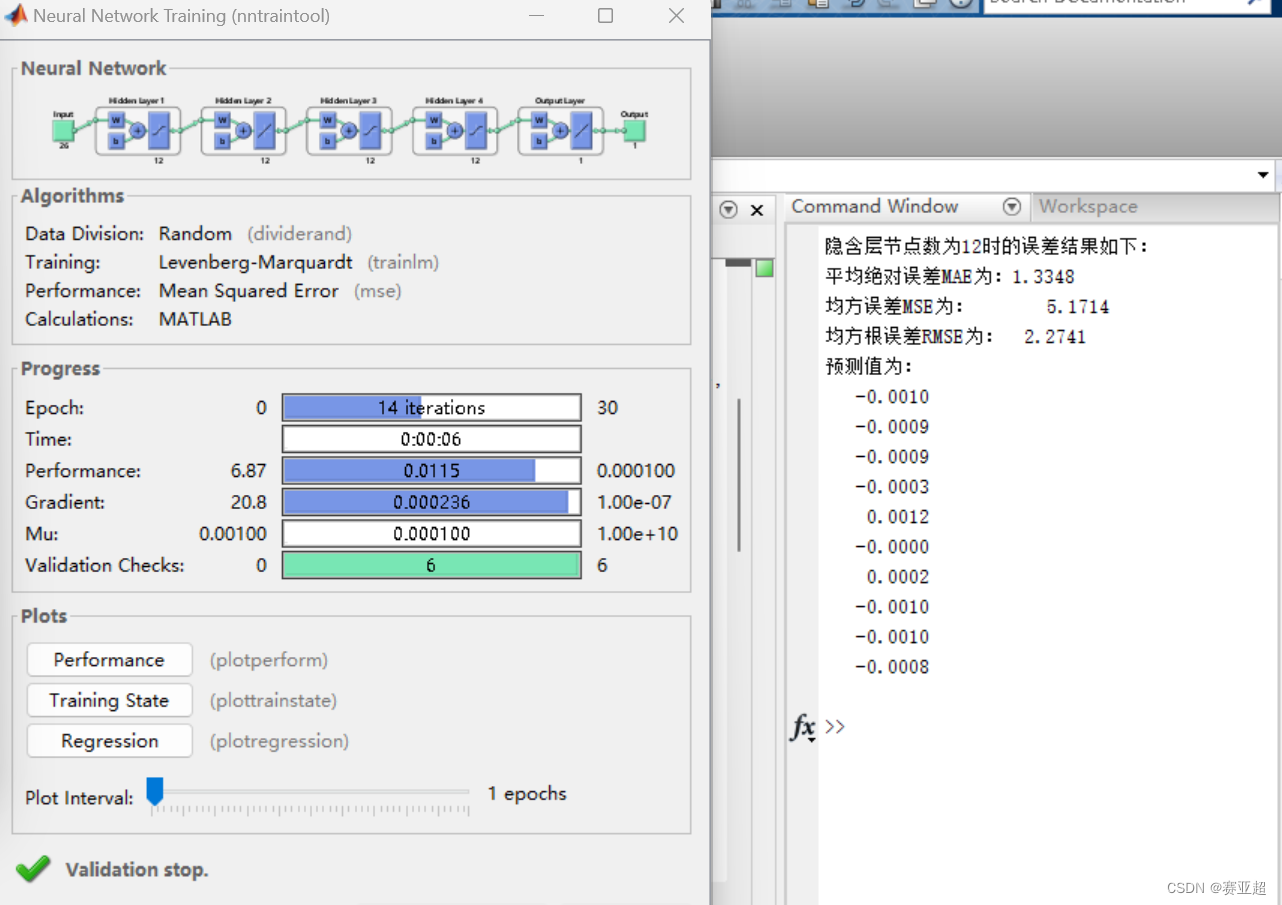
（2）再增加一层隐藏层

又增加一层之后发现预测值精度更高了，出现了0值得情况！说明增加网络深度对预测结果有很大帮助。

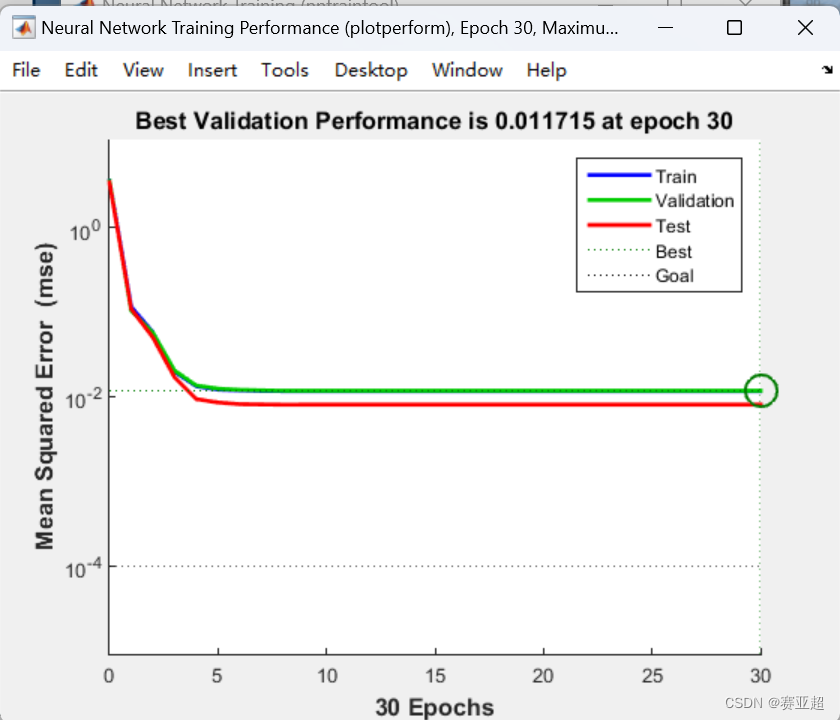
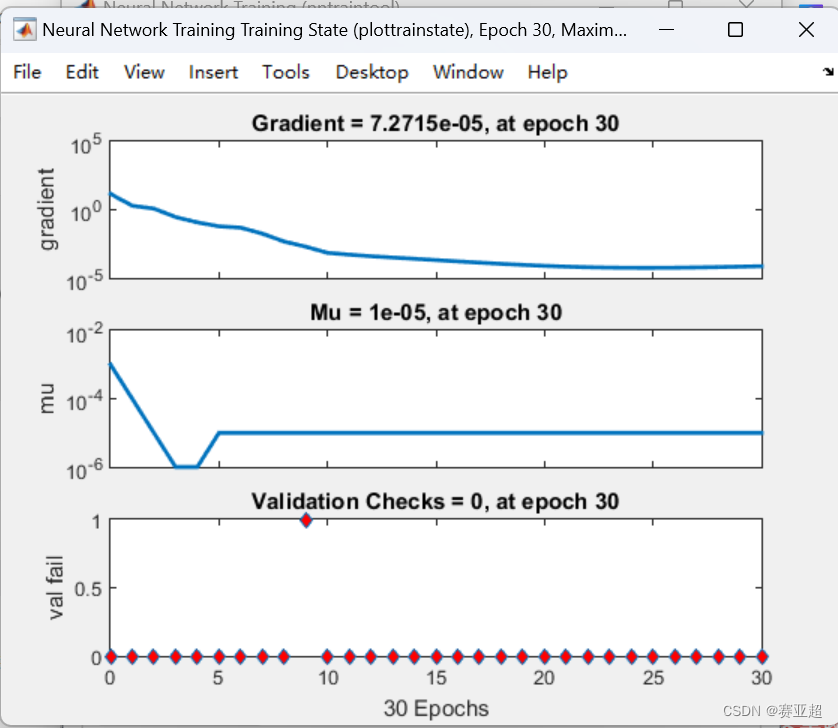
（3）再增加一层看看结果

可以看到增加到四层得出的预测值精度反而下降了，而且训练也没又迭代完。

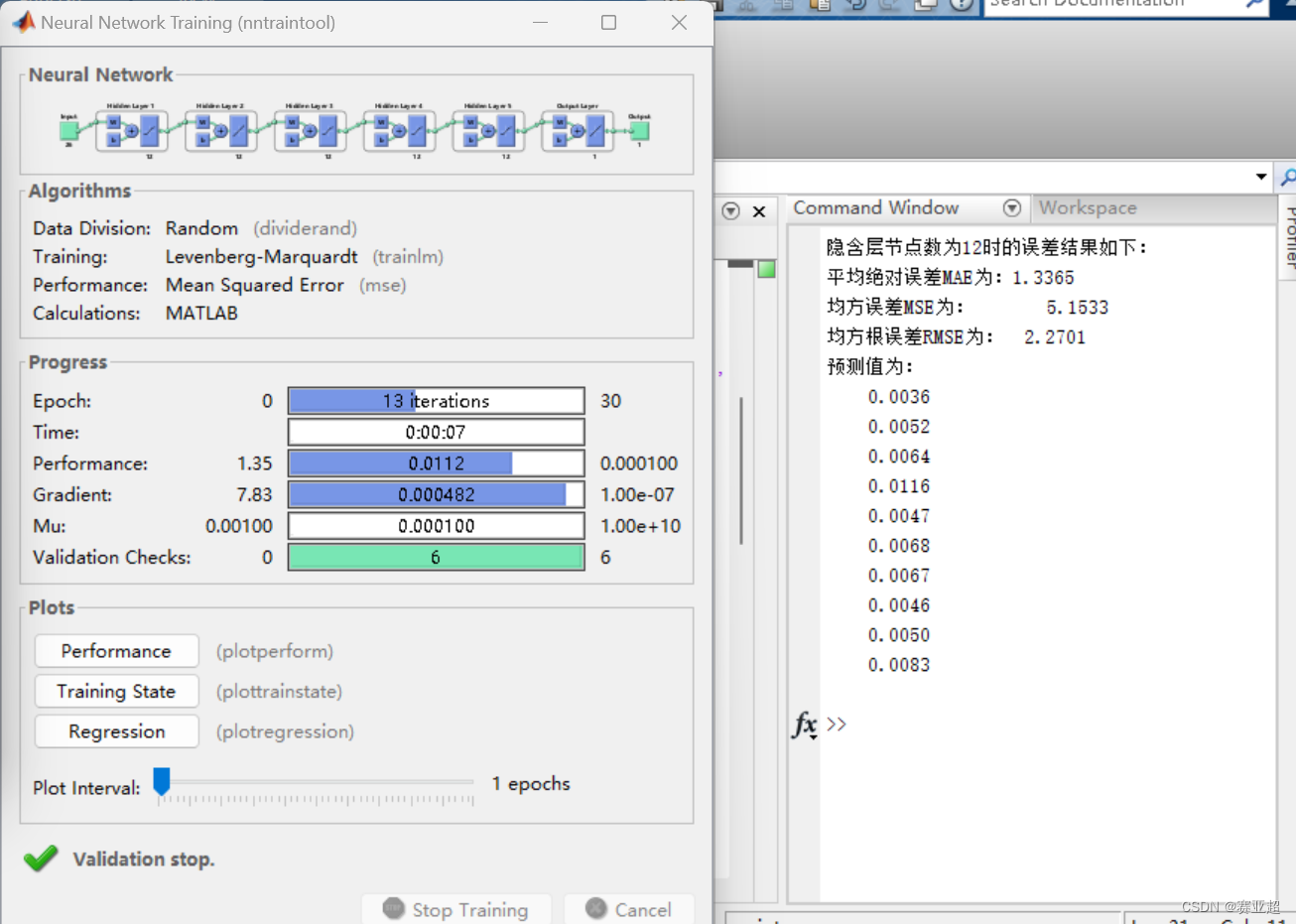
（4）增加到第五层试一下

随着层数的增加，训练时间增加，预测值的精度并没有变高，也没有训练完。

综上最佳层数是三层。之后通过改变隐藏层节点数来确定是否能提高其精度以及训练迭代完成。