1005. K 次取反后最大化的数组和
题目链接:1005. K 次取反后最大化的数组和
思路:取反k次,保证每次取反的数值是数组中的最小值,最后数组和就是最大的。
class Solution {public int largestSumAfterKNegations(int[] nums, int k) {for (int i = 0; i < k; i++) {int minIndex = 0;for (int j = 0; j < nums.length; j++) {if (nums[j] < nums[minIndex]) {minIndex = j;}}nums[minIndex] = -nums[minIndex];}int res = 0;for (int i = 0; i < nums.length; i++) {res += nums[i];}return res;}
}
代码随想录中本题的解题步骤为:
- 第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
- 第二步:从前向后遍历,遇到负数将其变为正数,同时K–
- 第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
- 第四步:求和
class Solution {public int largestSumAfterKNegations(int[] nums, int K) {// 将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小nums = IntStream.of(nums).boxed().sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1)).mapToInt(Integer::intValue).toArray();int len = nums.length;for (int i = 0; i < len; i++) {// 从前向后遍历,遇到负数将其变为正数,同时K--if (nums[i] < 0 && K > 0) {nums[i] = -nums[i];K--;}}// 如果K还大于0,那么反复转变数值最小的元素,将K用完if (K % 2 == 1) nums[len - 1] = -nums[len - 1];return Arrays.stream(nums).sum(); // 求和}
}
134. 加油站
题目链接:134. 加油站
思路:如果总油量减去总消耗量大于等于0,那么说明一定可以跑完一圈。从0开始累加每个加油站的剩余量记作curSum,一旦发现curSum小于0,说明[0, i]区间都不能作为起始位置,起始位置从i+1算起,重新累加curSum。
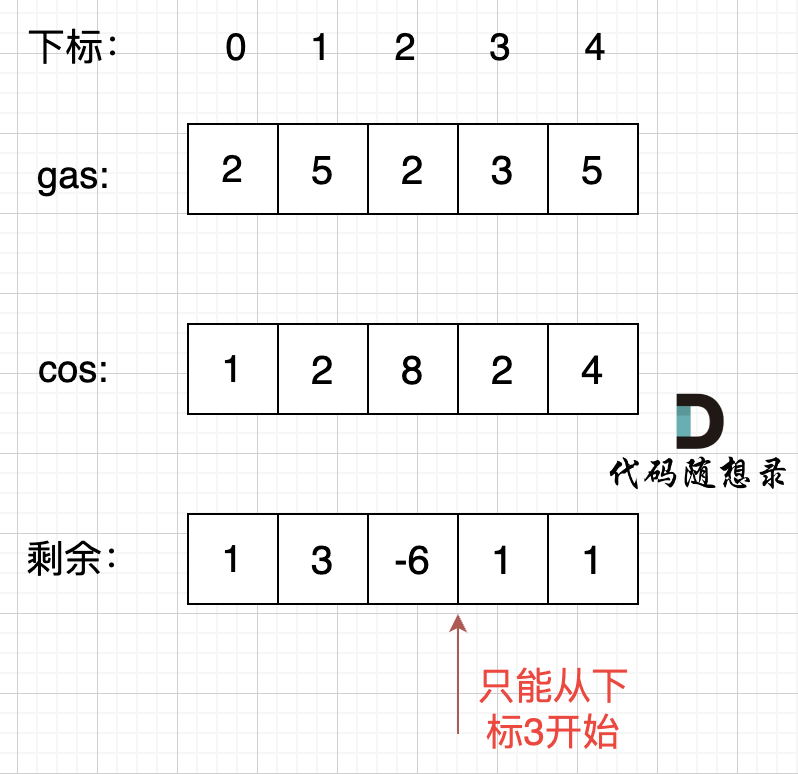
**局部最优:**当前curSum小于0,则[0, i]范围内无起始位置,起始位置至少是i+1;
**全局最优:**找到可以跑一圈的起始位置。
class Solution {public int canCompleteCircuit(int[] gas, int[] cost) {int curSum = 0;int totalSum = 0;int start = 0;for (int i = 0; i < gas.length; i++) {int temp = gas[i] - cost[i];totalSum += temp; // 累加所有的curSum += temp; // 累加当前的剩余汽油if (curSum < 0) { // 如果当前的汽油小于0了start = i + 1; // 更新起始位置curSum = 0; // 重新累加当前剩余汽油}}if (totalSum < 0)return -1; // 如果所有的汽油数小于消耗数一定不行。return start;}
}
135. 分发糖果
题目连接:135. 分发糖果
思路:采用两次贪心的策略:
- 一次是从左到右遍历,只比较右边孩子评分比左边大的情况。
- 一次是从右到左遍历,只比较左边孩子评分比右边大的情况。
从局部最优推出了全局最优,即:相邻的孩子中,评分高的孩子获得更多的糖果。
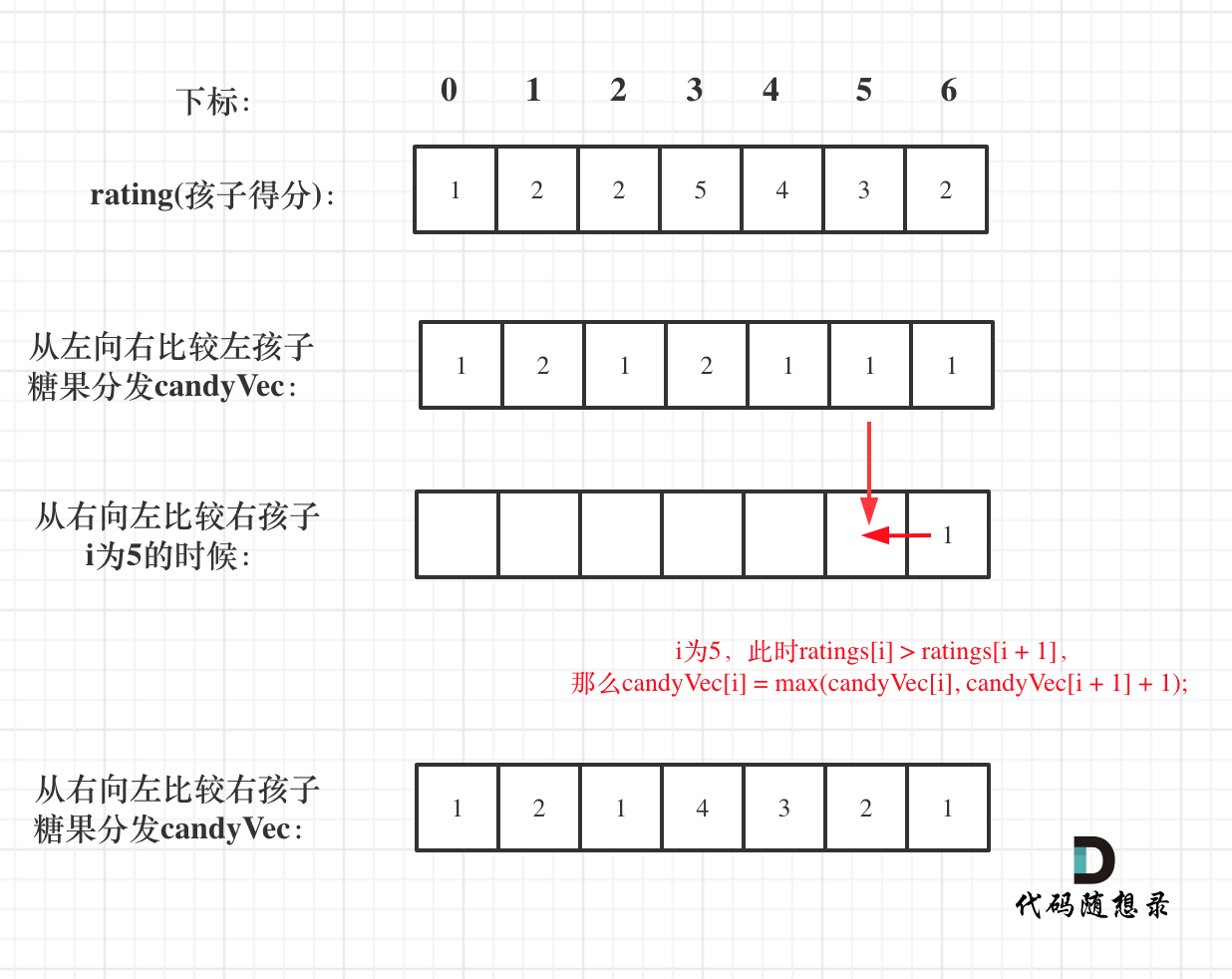
candy[i]只有取最大的才能既保持比左边candy[i - 1]的糖果多,也比右边candy[i + 1]的糖果多。
class Solution {public int candy(int[] ratings) {int[] candy = new int[ratings.length];// 先给每一个孩子分一个糖果for (int i = 0; i < candy.length; i++) {candy[i] = 1;}// 从前向后,右边孩子比左边大,就给右边孩子多一个for (int i = 1; i < candy.length; i++) {if (ratings[i] > ratings[i - 1]) {candy[i] = candy[i - 1] + 1;}}// 从后向前,左边孩子比右边大,就给左边孩子多一个// 此时左边需要考虑同时满足自己的左右两边// 取本身的糖果数(符合比它左边大) 和 右边糖果数 + 1 二者的最大值,// 这样才符合 它比它左边的大,也比它右边大for (int i = candy.length - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1] ) {candy[i] = Math.max(candy[i], candy[i + 1] + 1);}}// 计算结果int res = 0;for (int i = 0; i < candy.length; i++) {res += candy[i];}return res;}
}