一、ga句法结构

x = ga(fitnessfcn,nvars)
x = ga(fitnessfcn,nvars,A,b)
x = ga(fitnessfcn,nvars,A,b,Aeq,beq)
x = ga(fitnessfcn,nvars,A,b,Aeq,beg,IB,UB)
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon)
x = ga(fitnessfcn,nvars,A,b,Aeq,beq,LB,UB,nonlcon,options)
x = ga(fitnessfcn,nvars,A,b,[],[],LB,UB,nonlcon,IntCon)
x = ga(fitnessfcn,nvars,A,b,[],[],LB,UB,nonlcon,IntCon,options)
x = ga(problem)
[x,fval] = ga(fitnessfcn,nvars,...)
[x,fval,exitflag] = ga (fitnessfcn,nvars,...)
[x,fval,exitflag,output] = ga(fitnessfcn,nvars,...)
[x,fval,exitflag,output,population] = gafitnessfcn,nvars,...)
[x,fval,exitflag,output,population,scores] = ga(fitnessfcn,nvars,...)

二、释义及解读

• fitnessfcn 为适应度句柄函数（即：目标函数）;
• nvars 为目标函数自变量的个数;
• options 为算法的属性设置,该属性是通过函数gaoptimset赋予的；
• x 为经过遗传进化以后自变量最佳染色体返回值；
• fval 为最佳染色体的适应度；
• exitflag 为算法停止的原因；

• output 为输出的算法结构；

• population 为最终得到种群适应度的列向量（即当前群体，而群体里性能最好的个体，便是最优值点）；

• scores 为最终得到的种群（即：最优值点的目标函数取值）；

• $A$ 与 $b$：线性不等式约束 $A\ast x\le b$ 中的矩阵；
  （Note: If the problem has m linear inequality constraints and nvars variables. then A is a matrix of size m-by-nvars and b is a vector of length m. ga evaluates the matrix product A*x as if x is transposed (Ax’). ）

• $Aeq$ 与 $beq$：线性等式约束 $Aeq\ast x=beq$ 中的矩阵；
  （Note: ga does not enforce linear constraints to be satisfied when the PopulationType option is ‘bitstring’ or ‘custom’.）

• nonlcon：非线性约束约束，该函数返回两个输出，即：[c,ceq] = nonlcon(x) 。 需要注意：ga atempts to achieve $c=0$ and $ceq=0$. $c$ and ceg are row vectors when there are multiple constraints. Set unused outputs to [ ].

• IntCon：若变量 x 中存在整数变量，则在这里设置！具体地，IntCon 是由正数整数组成的向量，取值从 1 到 nvars，IntCon 中的每个值代表决策变量 x 中相应位置的索引变量是整数变量。
  （Note: When IntCon is nonempty, Aeq and beq must be empty ([ ]), and nonlcon must return empty for ceq. For more information on integer programming, see Mixed Integer Optimizaton.）

• options：Create options using gaoptimset. 下一章节将详细介绍 options 中关于 gaoptimset 的设置规则。

三、gaoptimset 介绍

gaoptimset 常用来设置 options 中的各个选项，其句式结构如下：

options = gaoptimset('param1',value1,'param2',value2,...)

其中， ‘Param1’、 ‘Param2’等是需要设定的参数，比如：种群规模（PopulationSize）、交叉比例(CrossoverFraction)等，value1、value2等则是Param的具体值，常用的参数名如下表：

设定的参数名（Param名）	说明	默认值
CrossoverFraction	交叉比例	0.8
Generations	算法中止的最大迭代次数	100
PopulationSize	种群规模	20
MigrationFraction	变异概率	0.2
FitnessLimit	当适应度函数达到设定的值时算法中止	-
StallGenLimit	当超过StallGenLimit代适应度函数为改善时，算法中止	50

更多参数设定详见 MATLAB 官方文档，可在MATLAB命令窗口中输入 “doc gaoptimset” 查看：

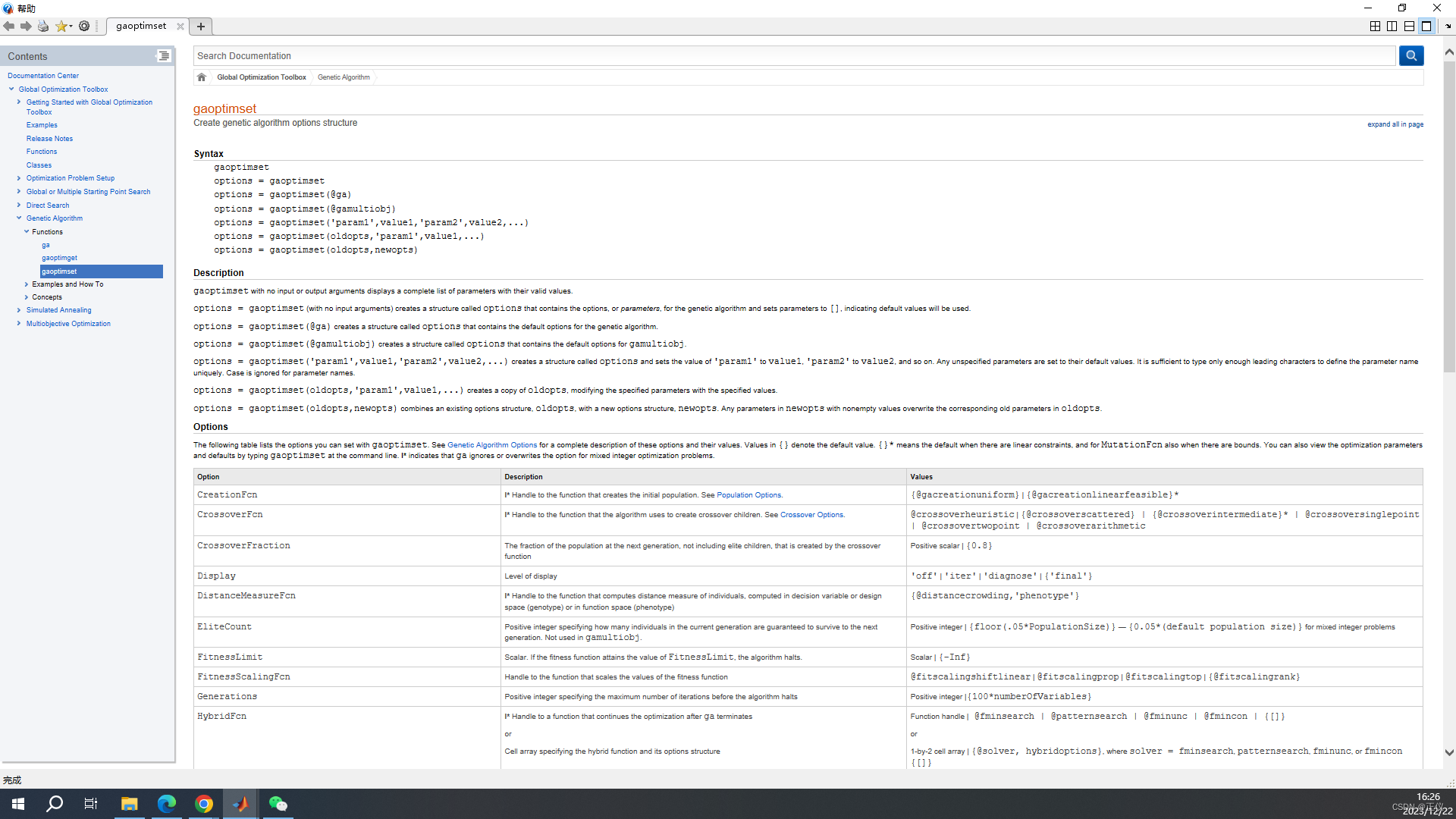
四、实例运行

实例原始网址： MATLAB利用遗传算法函数求目标函数的最优解

1. 目标函数如下：

function f = myfit( x )f = (339-0.01*x(1)-0.003*x(2))*x(1)...+ (399-0.004*x(1)-0.01*x(2))*x(2)...- (400000+195*x(1)+225*x(2));f = -f; %因为GA是寻找最小值，所以为了求这个函数的最大值，取f的相反数
end　

2. 主函数如下：

options = gaoptimset();
options.Generations = 2000; %最大迭代数设为2000%再次调用GA函数
[X,FVAL,EXITFLAG,OUTPUT] =ga(@myfit, 2 ,[], [],[],[],[],[],[],options)

运行结果为：

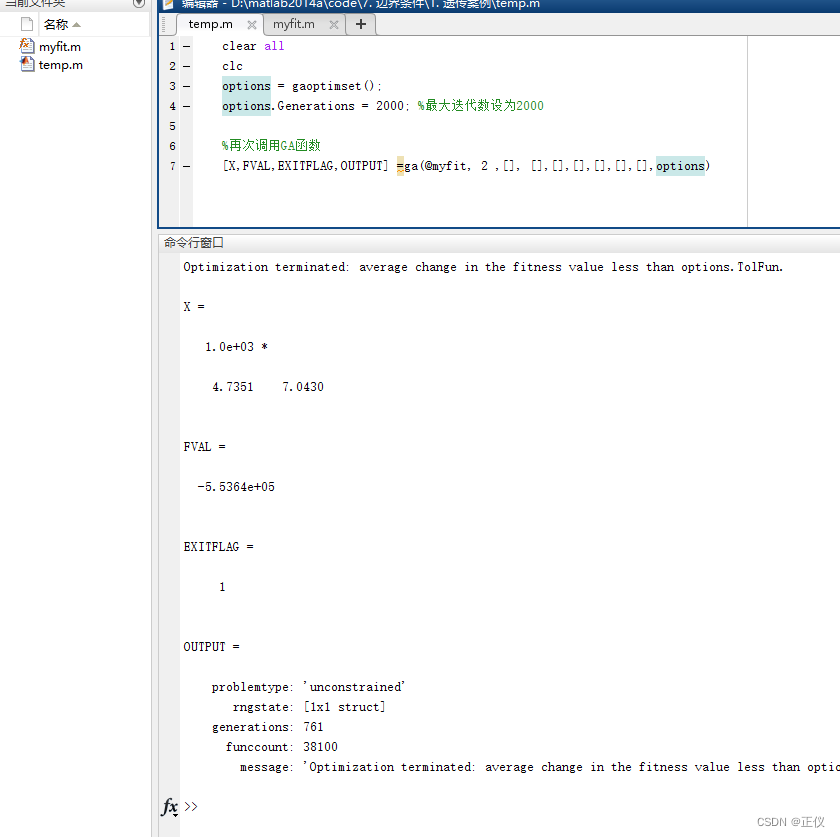
EXITFLAG 返回值为1，说明所求结果无特殊情况。

需要注意的是：如果 options.Generations 不设为 2000，采用默认迭代100轮来运行上述代码，则运行结果如下图所示：

注意到此时，EXITFLAG 返回值为0，显示信息为：Optimization terminated: maximum number of generations exceeded.

即：达到最大迭代轮数，此时的结果与最优理想结果相差甚远。由此例可知，关于最大迭代次数的设定，一定要小心，务必满足迭代次数的要求！