0x52 背包-编程知识

`0x52` 背包

背包是线性DP中一类重要而特殊的模型。

1. 0/1背包

0/1背包问题的模型如下：

给定 $N$ 个物品，其中第 $i$ 个物品的体积为 $V_i$ ，价值为 $W_i$ 。有一个容积为 $M$ 的背包，要求选择一些物品放入背包，使得物品总体积不超过 $M$ 的前提下，物品的价值总和最大。

根据上一节线性DP的知识，很容易想到依次考虑每个物品是否放入背包，用“已经处理的物品数”作为DP的“阶段”，以“背包中已经放入的物品总体积”作为附加维度。

$F [i, j]$ 表示从前 $i$ 个物品中选出了若干物品放入体积为 $j$ 的背包，物品的最大价值和。
$j]=\max \left\{\begin{array}{l} F[i-1, j] ,不选第i个物品 \\ F[i-1, j-V_i]+W_i ,选第i个物品 \end{array}\right.$
初值：未放入物品价值皆0，目标： $F [N] [M]$ 。

memset(f,0,sizeof(f)); 
for(int i=1;i<=n;++i)
{for(int j=0;j<=m;++j){f[i][j]=f[i-1][j];if(j>=v[i])f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);}
}

通过DP的状态转移方程，我们发现，每一阶段 $i$ 的状态只与上一个阶段 $i - 1$ 的状态有关。在这种情况下，可以使用称为“滚动数组”的优化方法，降低空间开销。

int f[2][MAX_M+1];
memset(f,0,sizeof(f));
for(int i=1;i<=n;++i)
{for(int j=0;j<=m;++j){f[i&1][j]=f[(i-1)&1][j];if(j>=v[i])f[i&1][j]=max(f[i&1][j],f[(i-1)&1][j-v[i]]+w[i]);}
}

在上面的程序中，我们把阶段 $i$ 的状态存储在第一维下标为 $i\&1$ 的二维数组中。当 $i$ 为奇数时， $i\&1$ 等于1；当 $i$ 为偶数时， $i\&1$ 等于0。因此，DP的状态就相当于在 $F [0] []$ 和 $F [1] []$ 两个数组中交替转移，空间复杂度从 $O (NM)$ 降低为 $O (M)$ 。

进一步分析发现，在每一个阶段开始时，实际上执行了一次从 $F [i - 1] []$ 到 $F [i] []$ 的拷贝操作。这提示我们进一步省略掉 $F$ 数组的第一维，只用一维数组，即当外层循环到 $i$ 个物品时， $F [j]$ 表示背包中放入总体积为 $j$ 的物品的最大价值和。

int f[MAX_M+1];
memset(f,0,sizeof(f));
f[0]=0;
for(int i=1;i<=n;++i)for(int j=m;j>=v[i];--j)f[j]=max(f[j],f[j-v[i]]+w[i]);

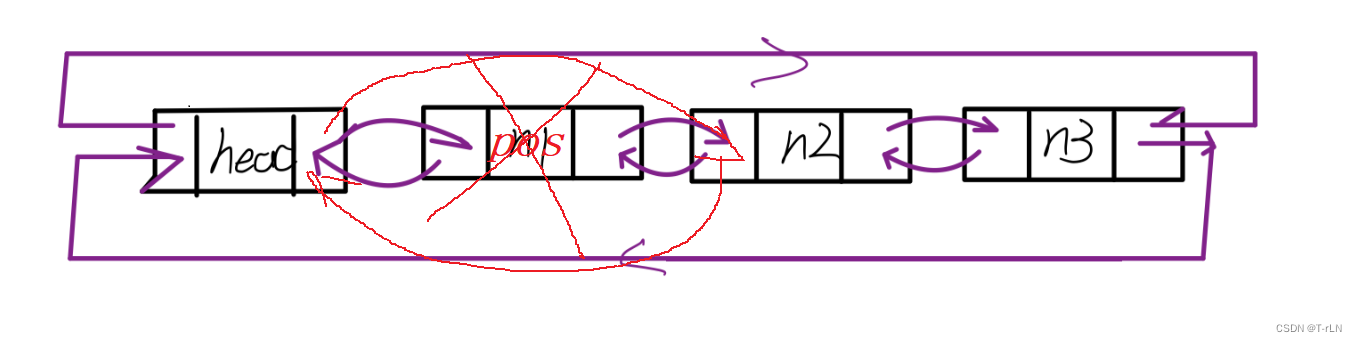
请注意上面的代码片段特别标注的部分——我们使用的了倒序循环。循环到 $j$ 时：

1. $F$ 数组的后半部分 $F[j\sim M]$ 处于“第 $i$ 个阶段”，也就是已经考虑过放入第 $i$ 个物品的情况。

2.前半部分 $F[0\sim j-1]$ 处于“第 $i - 1$ 个阶段”，也就是还没有第 $i$ 个物品更新。

接下来 $j$ 不断减小，意味着我们总是用“第 $i - 1$ 个阶段”的状态向“第 $i$ 个阶段”的状态进行转移，符合线性DP的原则，进而保证了第 $i$ 个物品只会被放入背包一次。如下图所示。

在这里插入图片描述

然而，如果使用正序循环，假设 $F [j]$ 被 $F[j-V_i]+W_i$ 更新，接下来 $j$ 增大到 $j+V_i$ 时， $F[j+V_i]$ 又可能被 $F[j]+W_i$ 更新。此时，两个都处于“第 $i$ 个阶段”的状态之间发生了转移，违背了线性DP的原则，相当于第 $i$ 个物品被使用了两次。如下图所示。

在这里插入图片描述

所以，在上面的代码中必须用到倒序循环，才符合0/1背包中每个物品是唯一的、只能放入背包一次的要求。

2.完全背包

完全背包问题的模型如下：

给定 $N$ 个物品，其中第 $i$ 个物品的体积为 $V_i$ ，价值为 $W_i$ ，并且有无数个。有一个容积为 $M$ 的背包，要求选择一些物品放入背包，使得物品总体积不超过 $M$ 的前提下，物品的价值总和最大。

先来考虑使用传统的二维线性DP的做法。设 $F [i, j]$ 表示从前 $i$ 个物品中选出了若干物品放入体积为 $j$ 的背包，物品的最大价值和。
$F[i,j]=\max \left\{\begin{array}{l} F[i-1,j],尚未选过第i种物品 \\ F[i,j-V_i]+W_i,{ if } \ j\geq V_i,从第i种物品中选一个 \end{array} \right.$
初值：未放入物品价值皆0，目标： $F [N] [M]$ 。

与0/1背包一样，我们也可以省略 $F$ 数组的 $i$ 这一维。根据我们在0/1背包中对循环顺序的分析，当采用正序循环时，就对应这每种物品可以使用无限次，也对应着 $F[i,j]=F[i,j-V_i]+W_i$ 这个在两个均处于 $i$ 阶段的状态之间进行转移的方程。

int f[MAX_M+1];
memset(f,0,sizeof(0));
for(int i=1;i<=n;++i)
{for(int j=v[i];j<=m;++j)f[j]=max(f[j],f[j-v[i]]+w[i]);
}

3.多重背包

多重背包问题的模型如下：

给定 $N$ 个物品，其中第 $i$ 个物品的体积为 $V_i$ ，价值为 $W_i$ ，并且有 $C_i$ 个。有一个容积为 $M$ 的背包，要求选择一些物品放入背包，使得物品总体积不超过 $M$ 的前提下，物品的价值总和最大。

直接拆分法

求解多重背包问题最直接的方法就是把第 $i$ 种物品看作独立的 $C_i$ 个物品，转化为共有 $\sum_{i=1}^N C_i$ 个物品的0/1背包问题进行计算，时间复杂度为 $O(M*\sum_{i=1}^N C_i)$ 。该算法把每种物品拆分成了 $C_i$ 个，效率较低。

unsigned int f[MAX_M+1];
memset(f,0,sizeof(f));
for(int i=1;i<=n;++i)for(int j=1;j<=c[i];++j)for(int k=m;k>=v[i];--k)f[k]=max(f[k],f[k-v[i]]+w[i]);

二进制拆分法

众所周知，从 $2^0,2^1,2^2,...,2^{k-1}$ 这 $k$ 个2的整数次幂中选出若干个相加，可以表示出 $0\sim 2^k-1$ 之间的任何整数。进一步地，我们求出满足 $2^0+2^1+...+2^p \leq C_i$ 的最大整数 $p$ ，设 $R_i=C_i-2^0-2^1-...-2^p$ ，那么：

1.根据 $p$ 的最大性，有 $2^0+2^1+...+2^{p+1} > C_i$ ，可推出 $2^{p+1}>R_i$ ，因此 $2^0,2^1,...,2^{p}$ 选出若干个相加可以表示出 $0\sim R_i$ 之间的任何整数。

2.从 $2^0,2^1,...,2^{p}$ 以及 $R_i$ 中选出若干个相加，可以表示出 $R_i\sim R_i+2^{p+1}-1$ 之间的任何整数，而根据 $R_i$ 的定义， $R_i+2^{p+1}-1=C_i$ ，因此 $2^0,2^1,...,2^{p},R_i$ 选出若干个相加可以表示出 $R_i\sim C_i$ 之间的任何整数。

综上所述，我们可以把数量 $C_i$ 的第 $i$ 种物品拆成 $p + 2$ 个物品，它们的体积分别为：
$2^0*V_i,2^1*V_i,..,2^p*V_i,R_i*V_i$
这 $p + 2$ 个物品可以凑成 $0\sim C_i*V_i$ 之间所有能被 $V_i$ 整除的数，并且不能凑成大于 $C_i*V_i$ 的数。这等价于原问题种体积为 $V_i$ 的物品可以使用 $0\sim C_i$ 次。该方法仅把每种物品拆成了 $O(logC_i)$ 个，效率较高。

for(int i=1;i<=n;++i)
{int sum=c[i];for(int j=1;j<=sum;j*=2){for(int k=m;k>=j*v[i];--k)f[k]=max(f[k],f[k-j*v[i]]+j*w[i]);sum-=j;}if(sum>0){int j=sum;for(int k=m;k>=j*v[i];--k)f[k]=max(f[k],f[k-j*v[i]]+j*w[i]);}
}

单调队列

使用单调队列优化的动态规划算法求解多重背包问题，时间复杂度可以进一步降低到 $O (NM)$ ，与0/1背包和完全背包中的DP算法的效率相同，我们将在0x59节中进行讲解。

4.分组背包

分组背包问题的模型如下：

给定 $N$ 组物品，其中第 $i$ 组有 $C_i$ 个物品。第 $i$ 组的第 $j$ 个物品的体积为 $V_{ij}$ ，价值为 $W_{ij}$ 。有一容积为 $M$ 的背包，要求选择若干个物品放入背包，使得每组至多选择一个物品并且物品总体积不超过 $M$ 的前提下，物品的价值总和最大。

仍然先考虑原始线性DP的做法。为了满足“每组至多选择一个物品”，很自然的想法就是利用“阶段”线性增长的特征，把“物品组数”作为DP的“阶段”，只要使用了一个第 $i$ 组的物品，就从第 $i$ 个阶段的状态转移到第 $i + 1$ 个阶段的状态。设 $F [i, j]$ 表示从前 $i$ 组中选出物品放入总体积为 $j$ 的背包中，物品的最大价值和。
$F[i,j]=\max \left\{\begin{array}{l} F[i-1,j],不选第i组的物品 \\ \underset{1\leq k \leq C_i} \max F[i-1,j-V_{ik}]+W_{ik},选第i组的某个物品k \end{array} \right.$
与前面几个背包模型一样，我们可以省略 $F$ 数组的第一维，用 $j$ 的倒序循环来控制“阶段 $i$ ”的状态只能从“阶段 $i - 1$ ”转移而来。

memset(f,0,sizeof(f));
for(int i=1;i<=n;++i)for(int j=m;j>=0;j--)for(int k=1;k<=c[i];++k)if(j>=v[i][k])f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);

除了倒序循环 $j$ 之外，对于每一组内 $c [i]$ 个物品的循环 $k$ 应该放在 $j$ 的内层。从背包的角度看，这是因为每组内至多选择一个物品，若把 $k$ 置于 $j$ 的外层，就会类似多重背包，每组物品在 $F$ 数组的转移上会产生累积，最终可以选择超过一个物品。从动态规划的角度， $i$ 是“阶段”， $i$ 与 $j$ 共同构成“状态”，而 $k$ 是“决策”——在第 $i$ 组内使用哪一个物品，这三者的顺序绝对不能混淆。