什么问题要用回溯?
暴力都解决不了的问题
组合、排列、切割、子集、棋盘,这些问题
如何理解回溯法?
回溯法比较抽象、困难,采用图形可以帮助理解,解决问题
解决方式:抽象为一个树型结构
模板
void backtarcking(参数(做题的时候慢慢写)){
if(终止条件){
收集结果。
}
//单层搜索逻辑
for(遍历集合的元素集){
处理节点;//13
递归操作;
回溯操作;//1(进行撤销3,方便下次组合成 12)
}
}
组合
77. 组合 - 力扣(LeetCode)
本题关于剪枝操作是大家要理解的重点,因为后面很多回溯算法解决的题目,都是这个剪枝套路。
对着 在 回溯算法理论基础 给出的 代码模板,来做本题组合问题,大家就会发现 写回溯算法套路。
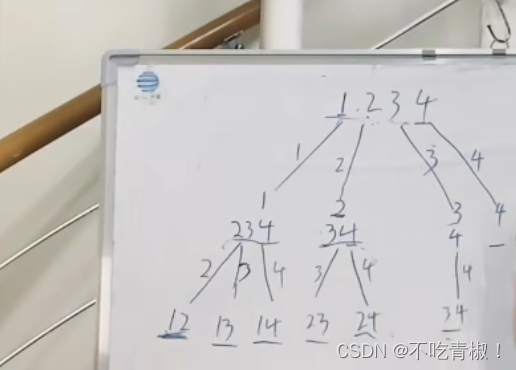
相当于通过递归来代替好多层的for循环
答案:(注意path要回溯,在堆里变化的,要回溯,回溯完之后就都为null了,所以要new一个)
class Solution {private List<Integer> path = new ArrayList<>();private List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> combine(int n, int k) {backingTracking(n,k,1);return result;}void backingTracking(int n,int k,int beginIndex){if(path.size()==k){//收割结果result.add(new ArrayList(path));return;}//单层递归逻辑//不是0开始,而是1for(int i = beginIndex;i<=n;i++){path.add(i);//递归backingTracking(n,k,i+1);//回溯path.removeLast();}}
}剪枝优化
对上一道题做优化,并分析剪枝的套路都有哪些。

回溯算法做剪枝,就是在for循环这里做文章,减小范围
要选k个元素,已经选了path.size(),还需要选取k-path.size个元素
例子:要从5个元素里面找3个元素,右面边界最多到5-3+1=3, a b c d e,也就是c的位置,因为从这之后,比如从d开始选,就小于3个了。这就是至多到n-(k-path.size())的原因
class Solution {private List<Integer> path = new ArrayList<>();private List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> combine(int n, int k) {backingTracking(n,k,1);return result;}void backingTracking(int n,int k,int beginIndex){if(path.size()==k){//收割结果result.add(new ArrayList(path));return;}//单层递归逻辑//不是0开始,而是1for(int i = beginIndex;i<=n-(k-path.size())+1;i++){path.add(i);//递归backingTracking(n,k,i+1);//回溯path.removeLast();}}
}