模型集成系列:Bagging和Boosting方法
本文讨论Bagging和Boosting。这些(Bagging和Boosting)是全世界数据科学家常用的术语。但是这些术语究竟是什么意思,它们如何帮助数据科学家。我们将学习关于bagging和boosting以及它们在实践中的应用。
笔记本目录
- 集成学习简介
- 自助法
- 装袋法
- 提升法
- 获取装袋法和提升法的N个学习器
- 加权数据元素
- 分类阶段的操作
- 选择最佳技术 - 装袋法还是提升法
- 装袋法和提升法的相似之处
- 装袋法和提升法的区别
- 总结和结论
- 参考文献
1. 集成学习简介
返回笔记内容
-
Bagging和boosting都是机器学习中的集成学习方法。
-
Bagging和boosting相似之处在于它们都是集成技术,通过将一组弱学习器组合起来,创建一个强学习器,其性能优于单个学习器。
-
集成学习通过组合多个模型来提高机器学习模型的性能。与单个模型相比,这种方法可以产生更好的预测性能。
-
集成学习的基本思想是学习一组分类器(专家)并允许它们进行投票。机器学习中的这种多样化是通过一种称为集成学习的技术实现的。这里的想法是训练多个模型,每个模型的目标是预测或分类一组结果。
-
Bagging和boosting是两种集成学习技术。这两种技术通过结合来自不同模型的多个估计值来减小单个估计值的方差。因此,结果可能是一个具有更高稳定性的模型。
-
学习中的主要错误原因是噪声、偏差和方差。集成有助于最小化这些因素。通过使用集成方法,我们能够增加最终模型的稳定性并减少先前提到的错误。
-
Bagging有助于减小模型的方差。
-
Boosting有助于减小模型的偏差。
-
-
这些方法旨在提高机器学习算法的稳定性和准确性。多个分类器的组合减小了方差,特别是在不稳定分类器的情况下,可能产生比单个分类器更可靠的分类结果。
-
要使用Bagging或Boosting,必须选择一个基学习算法。例如,如果我们选择分类树,Bagging和Boosting将包含一个树池,大小可以根据需要调整,如下图所示:

在理解bagging和boosting以及两种算法中如何选择不同的分类器之前,我们首先需要了解自助法(Bootstrapping)。
2. 自助法Bootstrapping
返回笔记内容
-
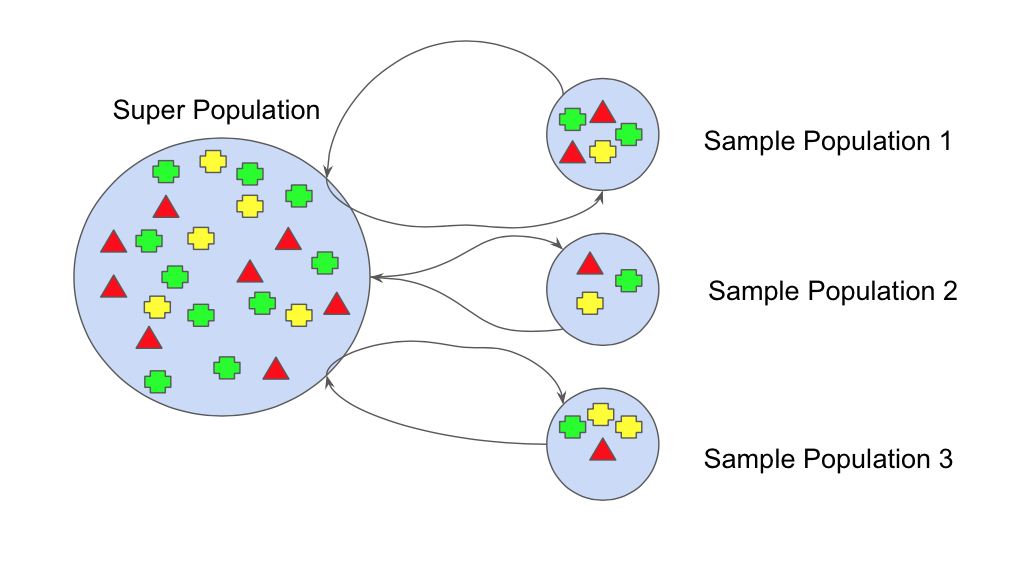
自助法是指带放回的随机抽样。自助法可以帮助我们更好地理解数据集的偏差和方差。
-
因此,自助法是一种抽样技术,我们从原始数据集中创建具有放回的观察子集。子集的大小与原始集合的大小相同。
-
自助法涉及从数据集中随机抽取小的数据子集。这个子集可以被替换。
-
数据集中的所有示例的选择具有相等的概率。这种方法可以帮助我们更好地理解数据集的均值和标准差。
-
假设我们有一个包含’n’个值(x)的样本,并且我们想要对样本的均值进行估计。我们可以按以下方式计算:
mean(x) = 1/n * sum(x) -
自助法可以用下图表示:
现在,我们将注意力转向bagging和boosting。
3. Bagging
返回笔记目录
-
Bagging(或称为自助聚合)是一种简单而非常强大的集成方法。Bagging是将自助法应用于高方差的机器学习算法,通常是决策树。
-
Bagging的思想是将多个模型的结果(例如,所有决策树)组合起来得到一个广义的结果。现在,引入自助法。
-
Bagging(或称为自助聚合)技术使用这些子集(袋)来对分布(完整集合)有一个公正的了解。用于Bagging的子集的大小可能小于原始集合。
-
可以表示如下:
**Bagging(装袋法)**的工作原理如下:
-
从原始数据集中创建多个子集,选择具有替换的观测值。
-
在每个子集上创建一个基本模型(弱模型)。
-
这些模型并行运行,彼此独立。
-
最终的预测结果是通过组合所有模型的预测结果来确定的。
现在,可以用下图来表示装袋法的过程:
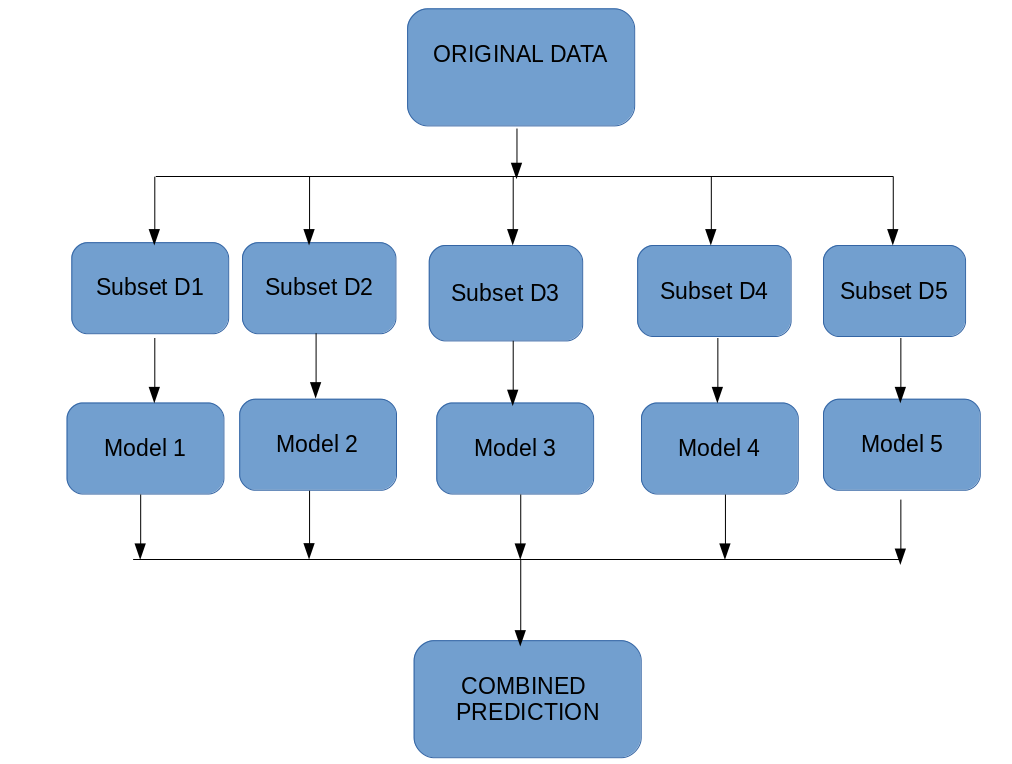
4. Boosting
返回笔记内容
-
提升是一个顺序过程,每个后续模型都试图纠正前一个模型的错误。后续模型依赖于前一个模型。
-
在这种技术中,学习者按顺序学习,早期学习者将简单模型拟合到数据中,然后分析错误的数据。换句话说,我们拟合连续的树(随机样本),在每一步中,目标是解决前一棵树的净误差。
-
当一个输入被一个假设错误分类时,它的权重增加,以便下一个假设更有可能正确分类它。通过在最后将整个集合组合起来,将弱学习者转化为性能更好的模型。
-
让我们通过以下步骤了解提升的工作方式。
-
从原始数据集中创建一个子集。
-
最初,所有数据点被赋予相等的权重。
-
在这个子集上创建一个基本模型。
-
使用该模型对整个数据集进行预测。
-
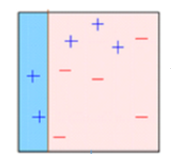
-
错误是通过使用实际值和预测值进行计算的。
-
预测错误的观测值将被赋予更高的权重。(在这里,三个被错误分类的蓝加号点将被赋予更高的权重)
-
创建另一个模型并对数据集进行预测。(该模型试图纠正前一个模型的错误)
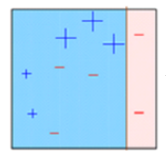
-
同样地,创建了多个模型,每个模型纠正前一个模型的错误。
-
最终模型(强学习器)是所有模型(弱学习器)的加权平均。
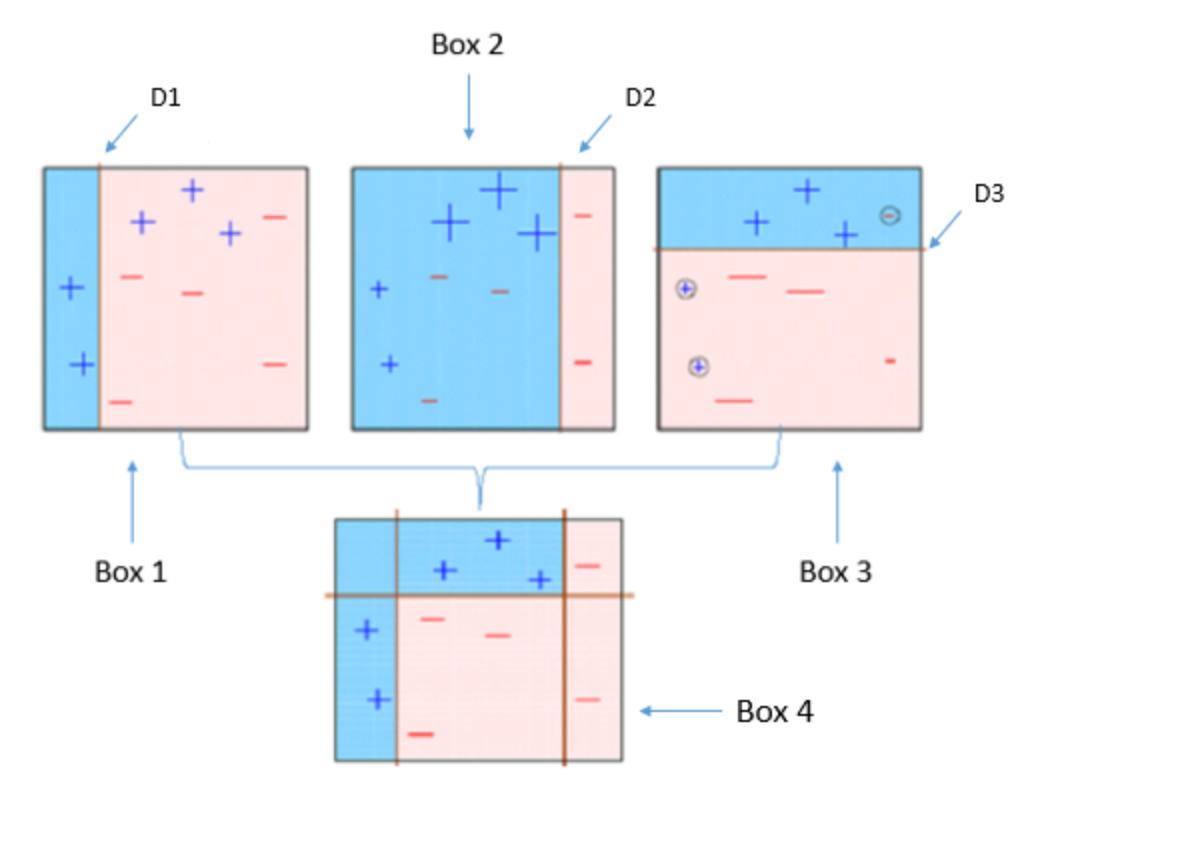
-
因此,提升算法将多个弱学习器组合成一个强学习器。
-
单个模型在整个数据集上表现不佳,但在数据集的某些部分上表现良好。
-
因此,每个模型实际上提升了集成的性能。
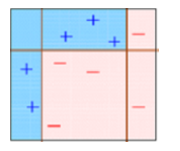
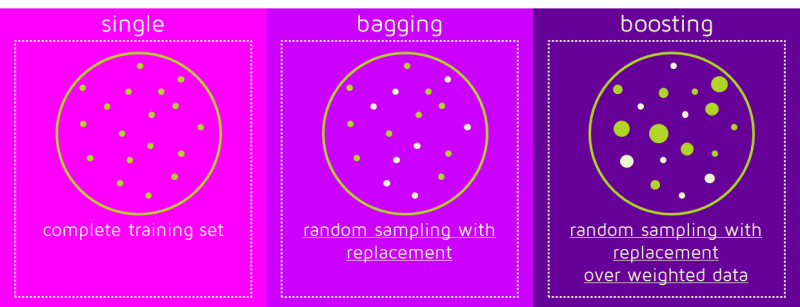
5. 获取用于Bagging和Boosting的N个学习器
返回笔记内容
-
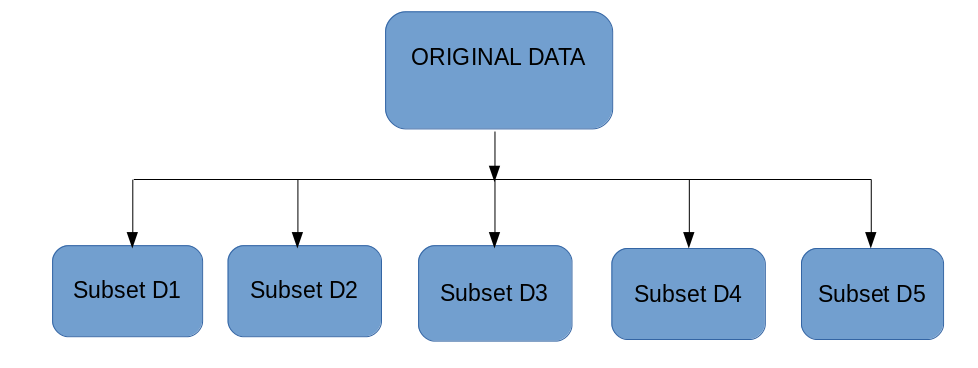
Bagging和Boosting通过在训练阶段生成额外的数据来获取N个学习器。
-
通过从原始数据集中进行有放回的随机抽样,产生N个新的训练数据集。
-
通过有放回的抽样,每个新的训练数据集中可能会有重复的观察结果。
-
在Bagging的情况下,任何元素在新的数据集中出现的概率相同。
-
然而,在Boosting的情况下,观察结果被赋予权重,因此其中一些观察结果会更频繁地出现在新的数据集中。
-
这些多个数据集用于训练相同的学习算法,因此会产生不同的分类器。
-
这个过程可以用下图表示:
6. 加权数据元素
返回笔记内容
-
现在,我们知道了这两种方法之间的主要区别。
-
在Bagging的训练阶段是并行的(即每个模型都是独立构建的),而Boosting则按照以下顺序顺序构建新的学习器:
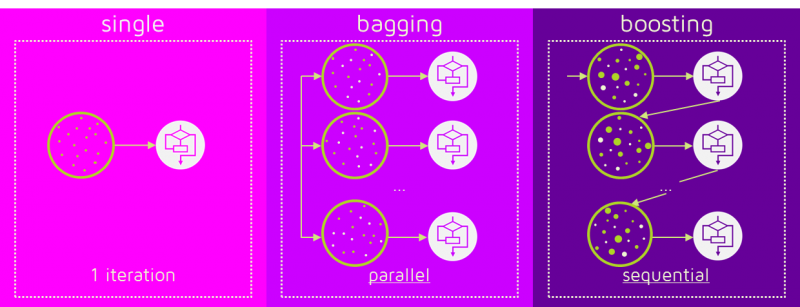
-
在Boosting算法中,每个分类器都是在数据上进行训练的,考虑了之前分类器的成功情况。
-
每次训练步骤之后,权重会重新分配。被错误分类的数据会增加其权重,以强调最困难的情况。
-
这样,后续的学习者在训练过程中会专注于这些情况。
7. 分类阶段的实际应用
返回笔记内容
-
要预测新数据的类别,我们只需要将N个学习器应用于新的观测数据。
-
在Bagging中,结果是通过对N个学习器的响应进行平均(或多数表决)得到的。
-
然而,Boosting会分配第二组权重,这次是为了N个分类器,以便对它们的估计值进行加权平均。
-
下图显示了这一过程的示意图:
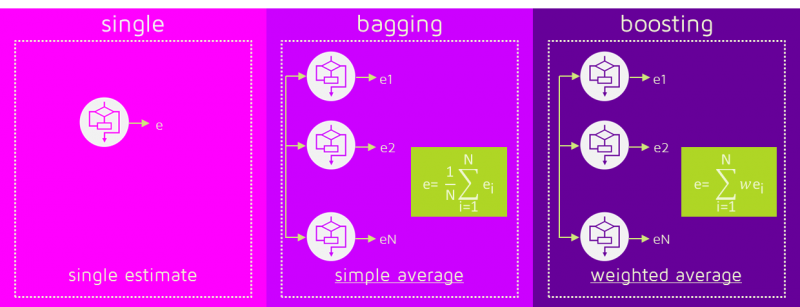
-
在Boosting训练阶段,算法为每个生成的模型分配权重。
-
在训练数据上具有良好分类结果的学习器将被分配比差的学习器更高的权重。
-
因此,在评估新的学习器时,Boosting也需要跟踪学习器的错误。
-
让我们看看这些过程的区别:
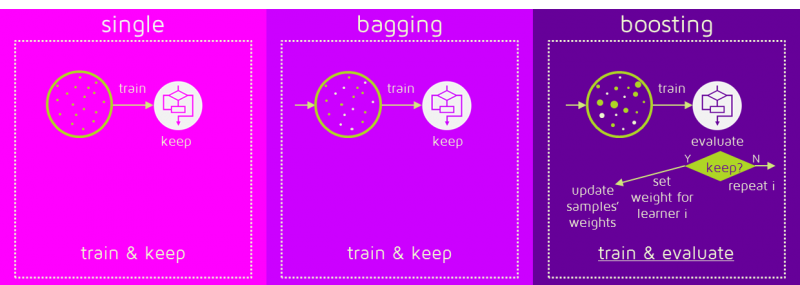
-
一些Boosting技术包括额外的条件来保留或丢弃单个学习器。
-
例如,在AdaBoost中,需要一个小于50%的错误率来维持模型;否则,迭代将重复进行,直到获得比随机猜测更好的学习器。
-
上图显示了Boosting方法的一般过程,但存在几种不同的替代方法,用于确定下一训练步骤和分类阶段中要使用的权重。
8. 选择最佳技术- Bagging还是Boosting
返回笔记内容
-
现在,我们可能会想到一个问题-在特定问题中选择Bagging还是Boosting。
-
这取决于数据、模拟和环境。
-
Bagging和Boosting通过结合来自不同模型的多个估计值来降低单个估计值的方差。因此,结果可能是一个具有更高稳定性的模型。
-
如果问题是单个模型的性能非常低,那么Bagging很少能获得更好的偏差。然而,Boosting可以生成一个组合模型,其错误率较低,因为它优化了单个模型的优势并减少了缺陷。
-
相反,如果单个模型的困难是过拟合,那么Bagging是最佳选择。而Boosting则无法帮助避免过拟合。
-
实际上,这种技术本身就面临着这个问题。因此,Bagging比Boosting更常有效。
9. Bagging和Boosting的相似之处
返回笔记内容
Bagging和Boosting的相似之处如下:
-
两者都是通过集成方法从一个学习器中获取N个学习器。
-
两者都通过随机抽样生成多个训练数据集。
-
两者通过对N个学习器进行平均(或者取大多数,即多数投票)来做出最终决策。
-
两者都擅长降低方差并提供更高的稳定性。
10. Bagging和Boosting的区别
返回笔记内容
Bagging和Boosting的区别如下:
-
Bagging是将属于同一类型的预测结果进行简单组合的方式,而Boosting是将属于不同类型的预测结果进行组合的方式。
-
Bagging旨在减少方差,而不是偏差,而Boosting旨在减少偏差,而不是方差。
-
在Bagging中,每个模型都获得相等的权重,而在Boosting中,模型的权重根据其性能进行加权。
-
在Bagging中,每个模型都是独立构建的,而在Boosting中,新模型受先前构建模型的性能影响。
-
在Bagging中,不同的训练数据子集是从整个训练数据集中随机抽取的,可以重复抽取。在Boosting中,每个新的子集都包含先前模型错误分类的元素。
-
Bagging试图解决过拟合问题,而Boosting试图减少偏差。
-
如果分类器不稳定(方差高),则应用Bagging。如果分类器稳定且简单(偏差高),则应用Boosting。
-
Bagging扩展到随机森林模型,而Boosting扩展到梯度提升模型。
11. 总结和结论
返回笔记目录
-
在这个内核中,我们讨论了两种非常重要的集成学习技术 - Bagging 和 Boosting。
-
我们详细讨论了 Bootstrapping,Bagging 和 Boosting。
-
我们讨论了分类阶段的实际应用。
-
然后,我们展示了如何为特定问题选择最佳技术 - Bagging 或 Boosting。
-
最后,我们讨论了 Bagging 和 Boosting 之间的相似性和差异。
-
我希望这篇文章能够让你对 Bagging 和 Boosting 有一个扎实的理解。
12. 参考资料
返回笔记目录
以下网站提供了本文中的思想、概念和图表:
-
https://quantdare.com/what-is-the-difference-between-bagging-and-boosting/
-
https://medium.com/swlh/difference-between-bagging-and-boosting-f996253acd22
-
https://www.geeksforgeeks.org/comparison-b-w-bagging-and-boosting-data-mining/
-
https://hub.packtpub.com/ensemble-methods-optimize-machine-learning-models/
-
https://towardsdatascience.com/decision-tree-ensembles-bagging-and-boosting-266a8ba60fd9
返回顶部