了解函数使用，对数学原理不一定要懂，

        这个软件包实现了各种邻居坐标计算函数以及用于散乱数据插值的不同方法。

        在2D欧几里得空间中，自然和常规邻居坐标的计算在“自然邻居坐标”一节中描述。

        在表面上的坐标和邻居计算在“表面自然邻居坐标和表面邻居”一节中讨论。

        最后，我们在“插值方法”一节中描述了此软件包提供的不同插值方法。

        散乱数据插值解决了以下问题：给定一组离散数据点上的函数度量，如何在任意查询点处插值此函数。

        更正式地说，设P={p1,…,pn}是在R2或R3中的一组n点，并且Φ是在P的凸包上的标量函数。

        我们假设函数值在P的点上是已知的，即对于每个pi∈P，我们关联zi=Φ(pi)。

        有时还需要在pi处知道Φ的梯度的知识。

        它被称为gi=∇Φ(pi)。

        插值是在P的凸包的任意查询点x上进行的。

1、天然临近坐标

        该软件包提供的大多数插值方法都依赖于二维自然和规则邻居坐标，我们将在本节中对此进行描述。

1.1、介绍

        Sibson  引入了自然邻近插值来插值多元散乱数据。给定一组数据点 P，与 P 相关的自然邻近坐标由 P 的 Voronoi 图定义。当模拟将查询点 x 插入 P 的 Voronoi 图时，x 的潜在 Voronoi 单元从相邻的现有单元中“窃取”了一些部分。

        2D示例：x有五个自然邻居p1，…，p5。自然邻居坐标λ3（x）是紫色多边形的面积π3（x，与总高亮区域的面积之比。 

        设π(x)表示x的潜在Voronoi单元的体积，πi(x)表示x的单元将从pi的单元中窃取的子单元的体积。x相对于数据点pi∈P的自然邻近坐标由下式定义

        二维示例如上图此外，

        各种论文表明，自然邻居坐标具有以下性质：

        x=∑ni=1λi(x)pi（重心坐标属性）。

        对于任何i，j≤n，λi(pj)=δij，其中δij是克罗内克符号。

        ∑ni=1λi(x)=1（单位分解属性）

        当查询点x位于P的凸包的包络上时，x的潜在Voronoi单元变为无穷大，并且：

        π(x)=∞

        λi(x)=0，对于P中的所有数据点pi，除了x所在边的两个端点 - 假设为p和q - 之外。

        x相对于这些端点p和q的自然邻居坐标为：

        Pipe证明了坐标函数在P的凸包中是连续的，并且除了在数据点P上是连续可微的。  

1.2、规则邻居坐标

        之前的定义自然地扩展到加权沃罗诺伊图。这些图也称为幂图，是通过考虑加权点（权重为标量）和考虑加权距离（幂距离）来获得的，幂距离是由Π((p,ωp),(q,ωq))=pq2−ωp−ωq定义的两个加权点（p,ωp）和（q,ωq）之间的距离。有关幂图的详细描述，请参阅软件包2D Triangulations的这一部分。

        常规邻居坐标的图示。点集与上图中的相同，但添加了权重。这些权重使用圆显示，每个圆的半径等于点权重的平方根。 

        警告：与沃罗诺伊图相反，加权点 pi 在 P 的幂图中不一定具有非空单元格（pi∈P）。在这种情况下，该点被称为隐藏点，其所有规则邻近坐标均为零。  

1.3、实施

        CGAL的插值包提供了计算二维点自然和规则邻近坐标的函数。请参考参考页 natural_neighbor_coordinates_2() 和 regular_neighbor_coordinates_2()。此外，该包还提供了在良好采样的点集曲面上计算自然邻近坐标的函数。

        给定一个Delaunay三角剖分或正则三角剖分，我们的实现分两步计算自然和正则的邻居坐标。首先，确定与查询点冲突的顶点（即查询点将“窃取”的顶点）。然后，通过对Voronoi子单元进行三角剖分来计算面积πi(x)。输出有三个方面：

        具有非零坐标的点（或顶点）以及这些坐标πi(x)，归一化因子π(x)，一个布尔指示符，指示坐标计算是否成功（相当于一个布尔值，指示查询点是否位于凸包中）。

        请注意，如果查询点已经在三角测量中定位（例如使用 locate() 等函数）和/或冲突区域的边界边已经确定，则替代函数允许避免重新计算（参见CGAL:natural_neighbor_coordinates_2() 和CGAL::regular_neighbor_coordinates_2()）。

2、表面天然邻近坐标

        本节介绍计算自然邻近坐标和与一组从曲面S发出的样本点相关的曲面邻近点的函数，并给出S上的查询点x。我们假设S是R3的闭紧曲面，并设P={p1，…，pn}为S的ε-样本（参见Amenta和Bern [1]）。这些概念基于Boissonnat和Flötotto 的定义。

2.1、介绍

        定义表面邻近点和表面邻近坐标的两条观察：

        首先，显然，在点x∈S的邻域内，曲面S的切平面Tx近似于S。如果曲面S相对于曲率和S的局部厚度采样良好，即它是一个ε-样本，那么切平面Tx与P∪{x}的Voronoi图的Voronoi单元的交集具有较小的直径。因此，在这个Voronoi单元内，切平面Tx是S的一个合理的近似。

        另外，第二条观察允许我们轻松计算这个交集图：我们可以使用毕达哥拉斯定理证明一个三维Voronoi图与一个平面H的交集是一个二维的幂图。定义幂图的点是P中的点投影到H上，每个点都以它到H的负平方距离进行加权。计算幂图的算法通过双正则三角剖分是众所周知的，例如由CGAL在类Regular_triangulation_2<Gt, Tds>中提供。

2.2、实施

Voronoi交集图

        在CGAL中，与平面H的3D Voronoi图交集对偶的正则三角剖分可以通过使用Voronoi_intersection_2_traits_3<K>特征类实例化Regular_triangulation_2<Gt, Tds>类来计算。该特征类包含一个点和一个向量作为类成员，它们定义了平面H。Regular_triangulation_2<Gt, Tds>使用的所有谓词和构造都被三维点上的相应运算符替换。

        例如，功率测试谓词（它取规则三角网的三个加权2D点p′、q′、r′，并测试第四个点t′相对于正交于p、q、r的功率圆的功率距离）被Side_of_plane_centered_sphere_2_3谓词替换，该谓词测试3D点t相对于以平面H为中心并通过3D点p、q、r的球体的位置。这种方法可以避免显式构造投影点和权重，这些操作非常容易产生舍入误差。

表面上的自然邻居坐标

        曲面上的自然邻近坐标的计算基于正则邻近坐标的计算，该坐标是通过函数regular_neighbor_coordinates_2()相对于正则三角剖分计算的，该三角剖分是与Tx和P的Voronoi图的交集Vor(P)∩Tx的对偶。

        当然，我们可以将所有数据点P引入到这个规则三角网中。但是，这不是必要的，因为我们只对x的单元感兴趣。保证查询点x的所有表面邻居都在作为参数传递给函数的输入点中就足够了。样本点P可以通过距离进行过滤，例如使用范围搜索或k-最近邻查询，或者在3D Delaunay三角网的帮助下进行过滤，因为表面邻居必然是该三角网中查询点自然邻居的子集。

        CGAL提供了一个函数，该函数封装了基于3D Delaunay三角网的过滤。对于按距离过滤的输入点，提供了函数，指示位于输入范围之外的点（即比最远输入点离x更远的点）是否仍然可以影响结果。这允许迭代地扩大输入点集，直到范围足以证明结果。

曲面邻居

        查询点的表面邻居是它在与 Vor(P)∩Tx 对偶的正则三角网中的邻居，Tx 和 P 的 Voronoi 图相交。至于表面邻居坐标，计算该正则三角网，并提供与上述数据点过滤和认证相同的数据点过滤。

3、插值方法

        我们在本节中介绍了该软件包提供的不同插值方法。这些可以重新组合为两大类：值和梯度插值方法。

3.1、函数值的插值  

        下面给出的插值函数用于插值函数值。

线性精度插值

        Sibson [定义了一个非常简单的插值函数，可以精确地再现线性函数。Φ(x)的插值被表示为相邻函数值的线性组合，由坐标加权

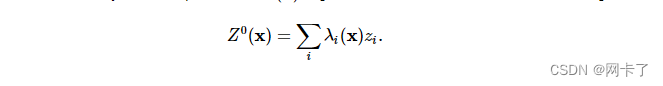
         事实上，如果对于x的所有自然邻点zi=a+btpi，则我们有

        通过重心坐标特性。

        这种插值是通过函数 CGAL::linear_interpolation()实现的。

二维散乱数据插值的插值方法

        Sibson描述了第二种插值方法，该方法也依赖于所有pi∈P的函数梯度gi。它在pi处具有梯度gi的C1连续性。Φ(x)=a+btx+γ xtx形式的球面二次曲面被精确再现。该证明依赖于自然邻近坐标的重心坐标性质，并假设Φ在数据点处的梯度已知或由函数值近似，如[9]所述（见梯度拟合部分）。

        Sibson的Z1插值是线性插值Z0和插值ξ的组合，ξ是第一阶函数的加权和

        Sibson观察到，如果Z0和ξ按照以下方式混合，则它们恰好可以重建一个球面二次曲面 

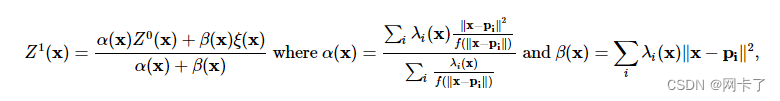
        其中，在Sibson的原作中，f（‖x−pi‖）=‖x–pi‖。

        可以通过调用CGAL::sibson_c1_interpolation() 使用此插值方法。

        CGAL中包含第二个使用f(∥x−pi∥)=∥x−pi∥2的实现，

        CGAL::sibson_c1_interpolation_square()，它对数字类型的要求较低，因为它避免了计算距离∥x−pi∥所需的平方根计算。理论保证是相同的（见[5]）。简单地说，f(0)附近的f斜率越小，x接近pi时插值函数越接近ξi。

Farin的C^1连续插值

        Farin的C^1连续插值（Farin's C^1 Continuous Interpolant）是一种插值方法，用于在二维或三维空间中创建平滑的曲线或曲面。该方法保证生成的插值函数在插值点处具有一阶导数的连续性，即C^1连续性。这种连续性确保曲线或曲面在插值点处光滑连接，不会出现尖锐的角或不平滑的转折。

        Farin[4]扩展了Sibson的工作，并通过在三次单形的伯恩斯坦-贝齐尔表示中嵌入自然邻近坐标来实现C1连续插值。如果已知数据点Φ的梯度，则该插值可以精确地再现二次函数。函数梯度可以通过Sibson'的方法（见梯度拟合部分）从函数值近似得到，该方法仅对球面二次曲面精确。

        Farin C1-连续插值函数在函数 CGAL::farin_c1_interpolation()中实现。

二次精度插值

        已知所有 pi∈P 的梯度 gi，我们构造了一个非常简单的插值函数，可以精确地再现二次函数。这个插值函数通常不是 C1 连续的。它的定义如下

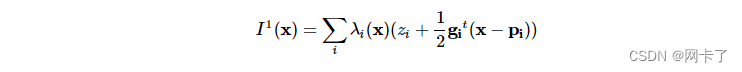
        此插值可以与方法CGAL::quadratic_interpolation（）一起使用。

3.2、渐变拟合

        Sibson描述了一种从数据点的函数值近似函数f的梯度的方法。对于数据点pi，我们确定

        其中λj(pi)是pi相对于与P∖{pi}关联的pi的自然邻近坐标。对于球面二次曲面，结果是精确的。 

        CGAL提供了近似位于凸包内部的所有数据点的梯度的函数。每种类型的相邻坐标都有一个函数：

        natural_neighbor_coordinate_2（）：CGAL::sibson_gradient_fating_nn_2（）

        regular_neighbor_coordinate_2（）：CGAL::sibson_gradient_fating_rn_2（）。

4、其他

        “Natural Neighbor Coordinates”翻译为“天然邻近坐标”。

        在地理信息系统（GIS）中，天然邻近坐标（Natural Neighbor Coordinates）是一种用于计算和表示不规则三角形网格（Triangulated Irregular Network, TIN）表面上点的位置的方法。它是一种插值方法，可以用于估算在三角形网格中的点的坐标。

        在天然邻近坐标中，每个点的位置由其最近的三角形定义，并且该点的位置是根据该三角形顶点的坐标和与该点最近的顶点的位置来计算的。这种方法可以提供比栅格方法更精确的表面表示，因为它可以更好地捕捉到表面的细节和特征。

        总之，“Natural Neighbor Coordinates”是GIS中用于计算和表示不规则三角形网格表面上点位置的一种方法。

        CGAL中的natural_neighbor_coordinates_2和regular_neighbor_coordinates_2是两种用于计算二维空间中点的邻居坐标的函数。

   natural_neighbor_coordinates_2：这个函数用于计算二维点集的自然邻居坐标。自然邻居坐标是一种插值方法，它基于Voronoi图来确定每个点对查询点的贡献。函数接受输入的点集和查询点，并返回查询点的自然邻居坐标。这些坐标表示查询点在由点集形成的Voronoi图中的位置，可以用于插值或其他几何计算。

   regular_neighbor_coordinates_2：这个函数用于计算二维点集的规则邻居坐标。规则邻居坐标是另一种插值方法，它基于Delaunay三角剖分来确定每个点对查询点的贡献。函数接受输入的点集和查询点，并返回查询点的规则邻居坐标。这些坐标表示查询点在由点集形成的Delaunay三角剖分中的位置，同样可以用于插值或其他几何计算。

        CGAL中的sibson_gradient_fating_nn_2和sibson_gradient_fating_rn_2是用于计算自然邻居插值（Natural Neighbor Interpolation）的梯度的函数。

   sibson_gradient_fating_nn_2：这个函数用于计算二维空间中自然邻居插值的梯度。它接受输入的点集、查询点、自然邻居坐标和权重，并返回查询点的自然邻居插值的梯度。梯度表示每个点对查询点的贡献的变化率，可以用于进一步的分析或优化。

   sibson_gradient_fating_rn_2：这个函数类似于sibson_gradient_fating_nn_2，但它用于计算一般规则（非自然）邻居插值的梯度。它接受输入的点集、查询点、规则邻居坐标和权重，并返回查询点的规则邻居插值的梯度。

        这两个函数在CGAL的插值包中提供，可以用于计算自然或规则邻居插值的梯度，从而进行进一步的优化或分析。它们基于Sibson的插值方法，并提供了高效和准确的计算结果。

CGAL 5.6 - 2D and Surface Function Interpolation: User Manual