104. 二叉树的最大深度
简单
给定一个二叉树
root,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
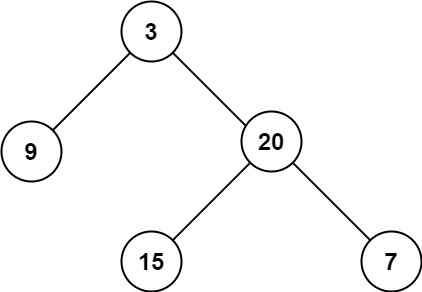
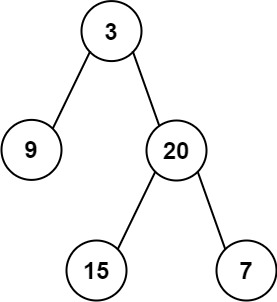
输入:root = [3,9,20,null,null,15,7] 输出:3示例 2:
输入:root = [1,null,2] 输出:2提示:
- 树中节点的数量在
[0, 104]区间内。-100 <= Node.val <= 100/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ int han(struct TreeNode *root) {if(root==NULL)return 0;int nums=0;nums=fmax(nums,han(root->left)+1);nums=fmax(nums,han(root->right)+1);return nums; }int maxDepth(struct TreeNode* root){if(root==NULL)return 0;return han(root); }
100. 相同的树
简单
给你两棵二叉树的根节点
p和q,编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
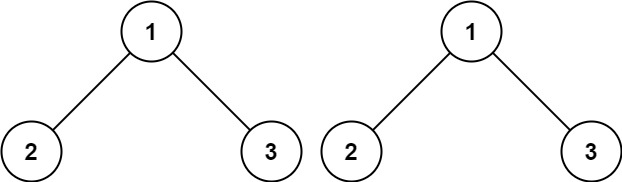
输入:p = [1,2,3], q = [1,2,3] 输出:true示例 2:
输入:p = [1,2], q = [1,null,2] 输出:false示例 3:
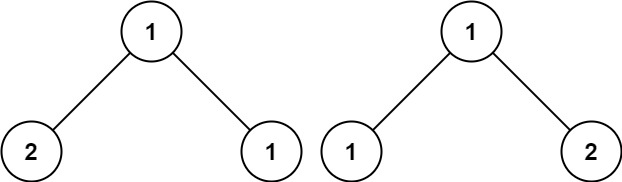
输入:p = [1,2,1], q = [1,1,2] 输出:false提示:
- 两棵树上的节点数目都在范围
[0, 100]内-104 <= Node.val <= 104/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ bool pan(struct TreeNode* p, struct TreeNode* q) {while(1){if(q==NULL&&p==NULL)return true;if(q==NULL||p==NULL)return false;if(q->val!=p->val){return false;}return pan(p->left,q->left)&&pan(p->right,q->right);}return true; }bool isSameTree(struct TreeNode* p, struct TreeNode* q){return pan( p, q); }
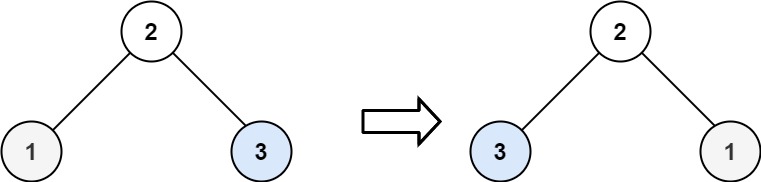
226. 翻转二叉树
简单
给你一棵二叉树的根节点
root,翻转这棵二叉树,并返回其根节点。示例 1:
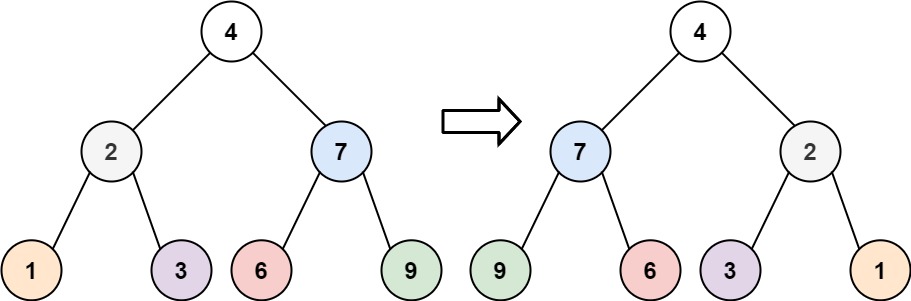
输入:root = [4,2,7,1,3,6,9] 输出:[4,7,2,9,6,3,1]示例 2:
输入:root = [2,1,3] 输出:[2,3,1]示例 3:
输入:root = [] 输出:[]提示:
- 树中节点数目范围在
[0, 100]内-100 <= Node.val <= 100/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ void Traversal(struct TreeNode* root) {if(root==NULL){return; }//左右子节点交换位置//自上而下struct TreeNode* temp;temp = root->left;root->left = root->right;root->right = temp;//左Traversal(root->left);//右Traversal(root->right); }struct TreeNode* invertTree(struct TreeNode* root) {Traversal(root);return root;}
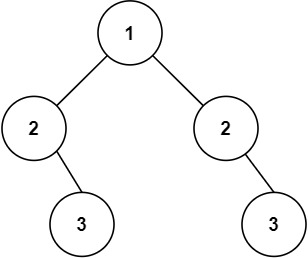
101. 对称二叉树
简单
给你一个二叉树的根节点
root, 检查它是否轴对称。示例 1:
输入:root = [1,2,2,3,4,4,3] 输出:true示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:false提示:
- 树中节点数目在范围
[1, 1000]内-100 <= Node.val <= 100/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ bool pan(struct TreeNode *q,struct TreeNode *p) {if(q==NULL&&p==NULL)return true;if(q==NULL||p==NULL)return false;if(q->val!=p->val)return false;return pan(q->left,p->right)&&pan(q->right,p->left); }bool isSymmetric(struct TreeNode* root){return pan(root->left,root->right); }
105. 从前序与中序遍历序列构造二叉树
中等
给定两个整数数组
preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]示例 2:
输入: preorder = [-1], inorder = [-1] 输出: [-1]提示:
1 <= preorder.length <= 3000inorder.length == preorder.length-3000 <= preorder[i], inorder[i] <= 3000preorder和inorder均 无重复 元素inorder均出现在preorderpreorder保证 为二叉树的前序遍历序列inorder保证 为二叉树的中序遍历序列/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ int pSize; int iSize;//自上往下void bt(struct TreeNode* root,int* preorder,int startp, int preorderSize, int* inorder,int starti, int inorderSize) {if(starti>inorderSize||startp>preorderSize||preorderSize>=pSize||inorderSize>=iSize){free(root);return;}root->val=preorder[startp];int i=starti;for(;i<inorderSize;i++){if(preorder[startp]==inorder[i]){break;}}if(!((starti)>(i-1)||(startp+1)>(i-starti+startp)||(i-starti+startp)>=pSize||(i-1)>=iSize)){root->left=(struct TreeNode*)calloc(1, sizeof(struct TreeNode));bt(root->left,preorder,startp+1,i-starti+startp,inorder,starti,i-1);} if(!((i+1)>inorderSize||(i-starti+startp+1)>preorderSize||preorderSize>=pSize||inorderSize>=iSize)){root->right=(struct TreeNode*)calloc(1, sizeof(struct TreeNode));bt(root->right,preorder,i-starti+startp+1,preorderSize,inorder,i+1,inorderSize); }} struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize) {struct TreeNode* root = (struct TreeNode*)calloc(1, sizeof(struct TreeNode));if(root==NULL){printf("错误\n");}pSize=preorderSize;iSize=inorderSize;bt(root,preorder,0,preorderSize-1,inorder,0,inorderSize-1);return root;}