核方法：多项式核函数-编程知识

核方法：多项式核函数

一、定义

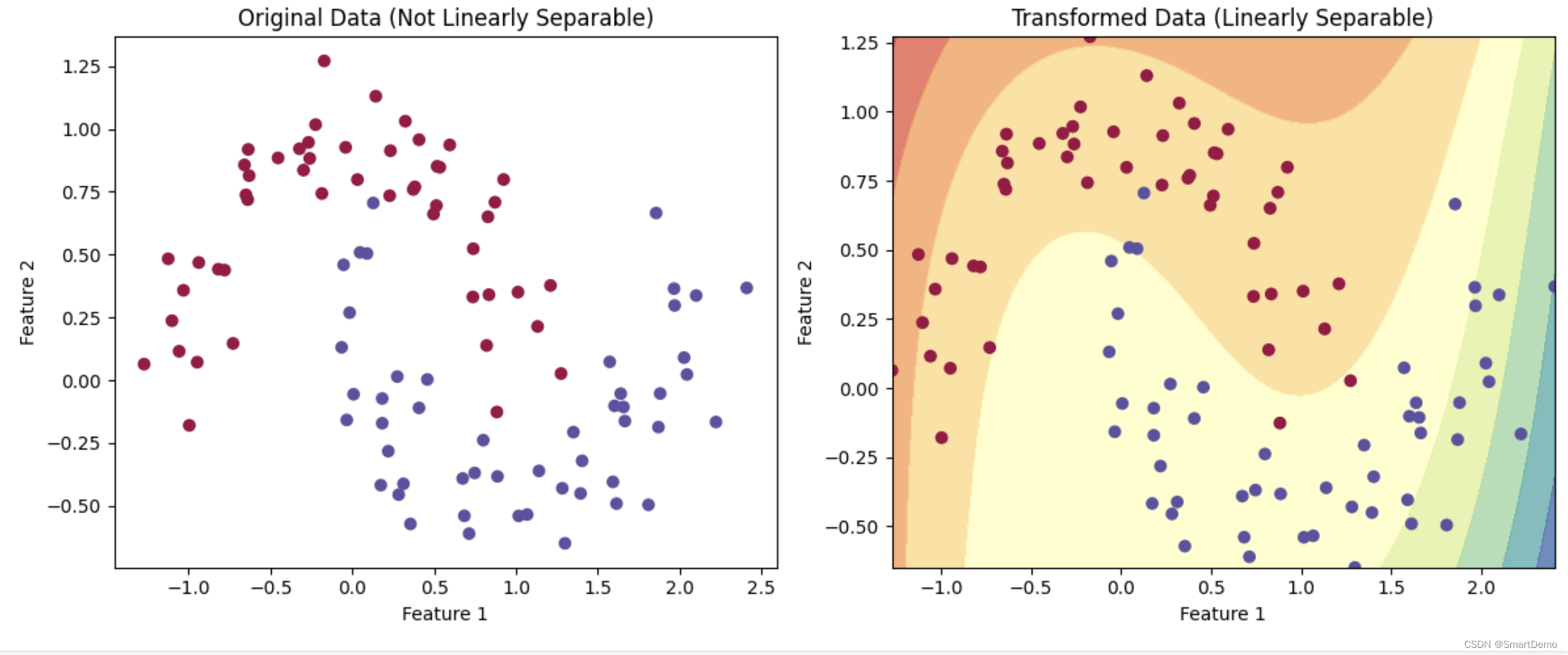
多项式核函数：将数据映射到高维空间，从而实现 低维线性不可分到高维线性可分

二、核心代码介绍

1、关于 svm_clf.decision_function ：

2、关于 PolynomialFeatures(degree=3) ：

二、全量代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.preprocessing import PolynomialFeatures
from sklearn.svm import SVCdef generate_non_linear_data():# 生成线性不可分的二维数据X, y = make_moons(n_samples=100, noise=0.15, random_state=42)return X, ydef plot_original_data(X, y):# 绘制原始数据（处理前）plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)plt.title("Original Data (Not Linearly Separable)")plt.xlabel("Feature 1")plt.ylabel("Feature 2")def train_svm_with_polynomial_kernel(X, y):# 创建多项式核函数对象（将数据映射到更高维度）poly_kernel = PolynomialFeatures(degree=3)X_poly = poly_kernel.fit_transform(X)# 使用支持向量机分类器（SVC）进行训练svm_clf = SVC(kernel="linear")svm_clf.fit(X_poly, y)return svm_clfdef plot_transformed_data(svm_clf, X, y):# 创建一个网格来覆盖数据的特征空间xx, yy = np.meshgrid(np.linspace(X[:, 0].min(), X[:, 0].max(), 200),np.linspace(X[:, 1].min(), X[:, 1].max(), 200))# 对网格中的每个点进行预测，确定其所属类别Z = svm_clf.decision_function(poly_kernel.transform(np.c_[xx.ravel(), yy.ravel()]))Z = Z.reshape(xx.shape)# 绘制处理后的数据（处理后）plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral, alpha=0.8)plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Spectral)plt.title("Transformed Data (Linearly Separable)")plt.xlabel("Feature 1")plt.ylabel("Feature 2")def main():# 生成非线性数据X, y = generate_non_linear_data()# 绘制原始数据plt.figure(figsize=(12, 5))plt.subplot(1, 2, 1)plot_original_data(X, y)# 训练 SVM 模型并绘制决策边界svm_clf = train_svm_with_polynomial_kernel(X, y)plt.subplot(1, 2, 2)plot_transformed_data(svm_clf, X, y)plt.tight_layout()plt.show()if __name__ == "__main__":main()

三、结果展示