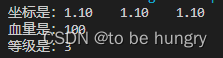
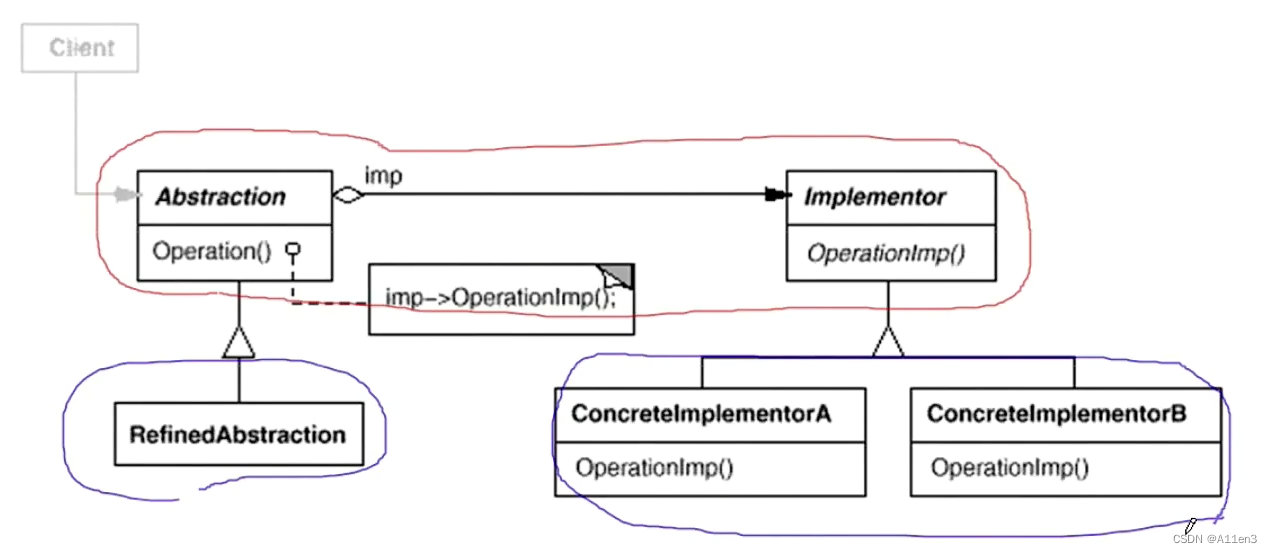
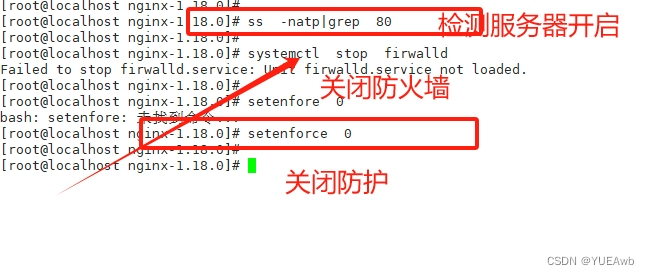
整体效果:
HTML部分:
<div class="lazy-box"><img class="lazy" data-original="img/1.jpg" alt="1.jpg" width="960" height="540"><img class="lazy" data-original="img/2.jpg" alt="2.jpg" width="960" height="540"><img class="lazy" data-original="img/3.jpg" alt="3.jpg" width="960" height="540"><img class="lazy" data-original="img/4.jpg" alt="4.jpg" width="960" height="540"><img class="lazy" data-original="img/5.jpg" alt="5.jpg" width="960" height="540"></div>
.lazy-box {margin: 0px auto;padding: 0px;width: 960px;height: auto;}.lazy-box>img {outline: none;margin: 25px auto;padding: 0px;border: 1px solid #E0E0E0;background-color: #F0F0F0;}
JS部分:
$(document).ready(function() {$("div.lazy-box>img.lazy").lazyload({effect: 'fadeIn',placeholder: 'img/loading.jpg'});});


![NNDL 作业12-优化算法2D可视化 [HBU]](https://img-blog.csdnimg.cn/direct/f48af9e9ec4848a68cc30e2e114fb0c9.png)