FHE简介-编程知识

FHE简介

1. 引言

加密技术已经存在了数千年，用于相互发送秘密信息。例如，凯撒密码是最早的加密技术之一，可以追溯到公元前60年，其只由字母表中的字母交换组成。

随着互联网的出现，人们生成的私人数据量呈指数级增长，数据泄露和大规模监控也随之大幅增加。为此，发明了新的加密技术——最终在日常应用程序中主流采用的端到端加密。

但是端到端加密实际上是如何工作的呢？它将如何改变人们使用互联网的方式？

当今的数据保护方式为：
在这里插入图片描述
由于数据在处理过程中是未加密的，数据仍可被窃取。根据IBM 2023 Security report，有：

当前涉及存储在云中数据的违规百分比为85%。
2023年数据泄露的全球平均总成本月为445万美金。
一家公司识别数据泄露所需的平均时长为277天。

现如今，对end-to-end（端到端）加密的需求迫在眉睫。

2. 同态加密简介

Fully Homomorphic Encryption（FHE），支持在不解密数据的情况下，对已加密数据进行处理。即意味着公司可在不窥探用户数据的情况下，为用户提供服务，且用户从功能上的体验是无差异的。

在数据传输和处理过程中，均使用的是已加密数据，这样链上不再仅是发送信息，而是端到端加密。

这不是黑魔法。
借助同态加密，可在不泄露任何个人数据的情况下使用任何线上服务。

从用户角度来看，服务不会改变：

可一如既往地使用它。

但从服务端的角度来看：

一切都是加密的——没有公司、政府或黑客能看到用户的数据。

3. FHE将如何改变未来

3.1 预防医学

想象一下，提前知道需做什么才能在一生中保持健康。人工智能越来越有可能做到这一点，但需要共享你所有的健康数据——从你的DNA到你的病史再到你的生活习惯。有了FHE，你可以在加密的同时发送所有这些数据，人工智能会以加密的健康建议做出回应，只有你才能看到。

如可推广为加密敏感数据的情感分析：
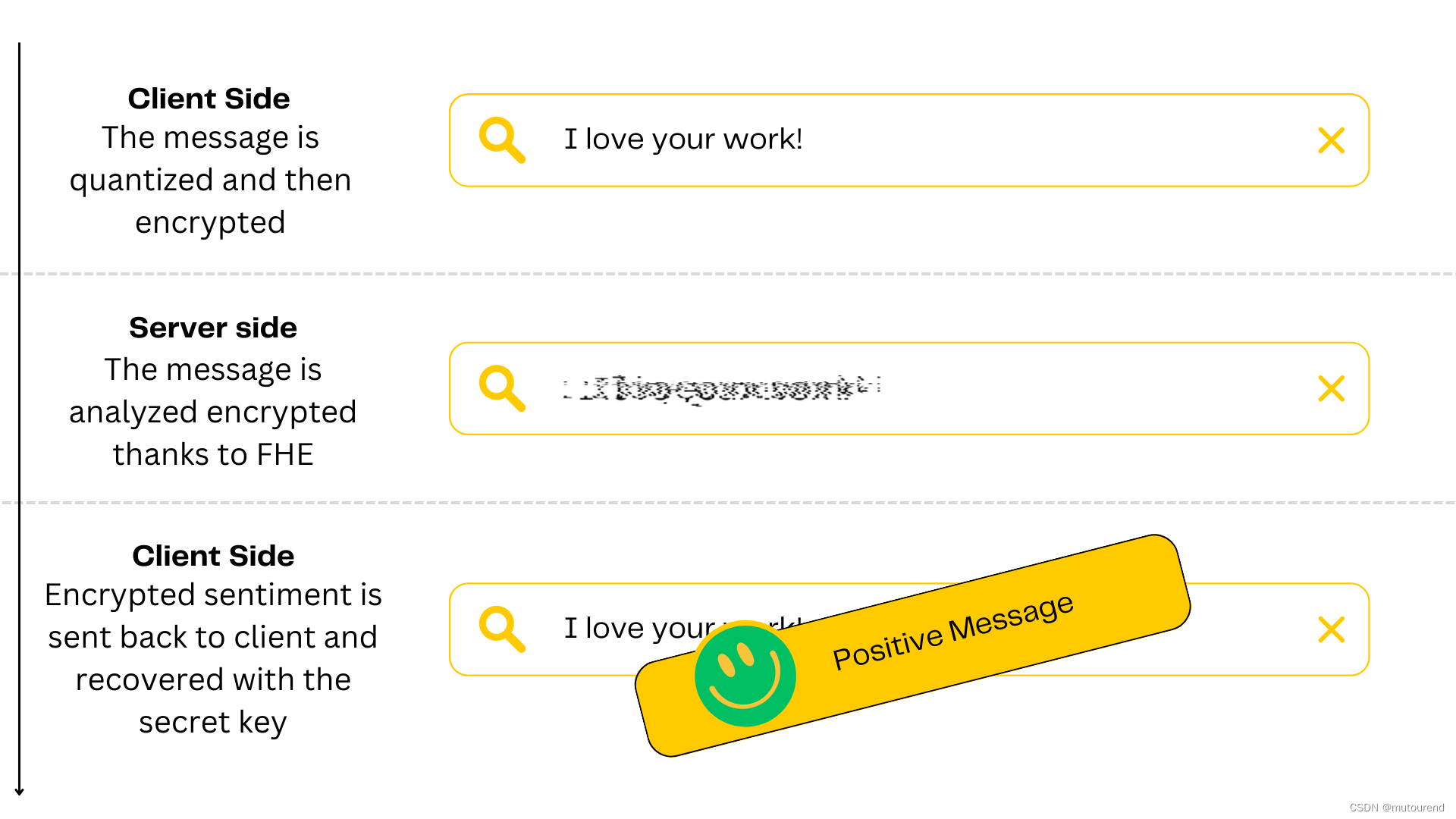
在这里插入图片描述

3.2 人脸识别

从科幻照进现实，人脸识别现在已成为人们日常体验的一部分。使用人脸识别进入建筑物，解锁手机，在照片中标记人物，并很快登录到各地的网站。然而，这需要有人拥有你的生物特征，如果掌握错误，该生物特征可能会被用来冒充你。使用FHE，可安全地进行身份验证，而不会有人窃取你的生物特征数据。

推广为加密图像处理，如加密图像数据滤波：
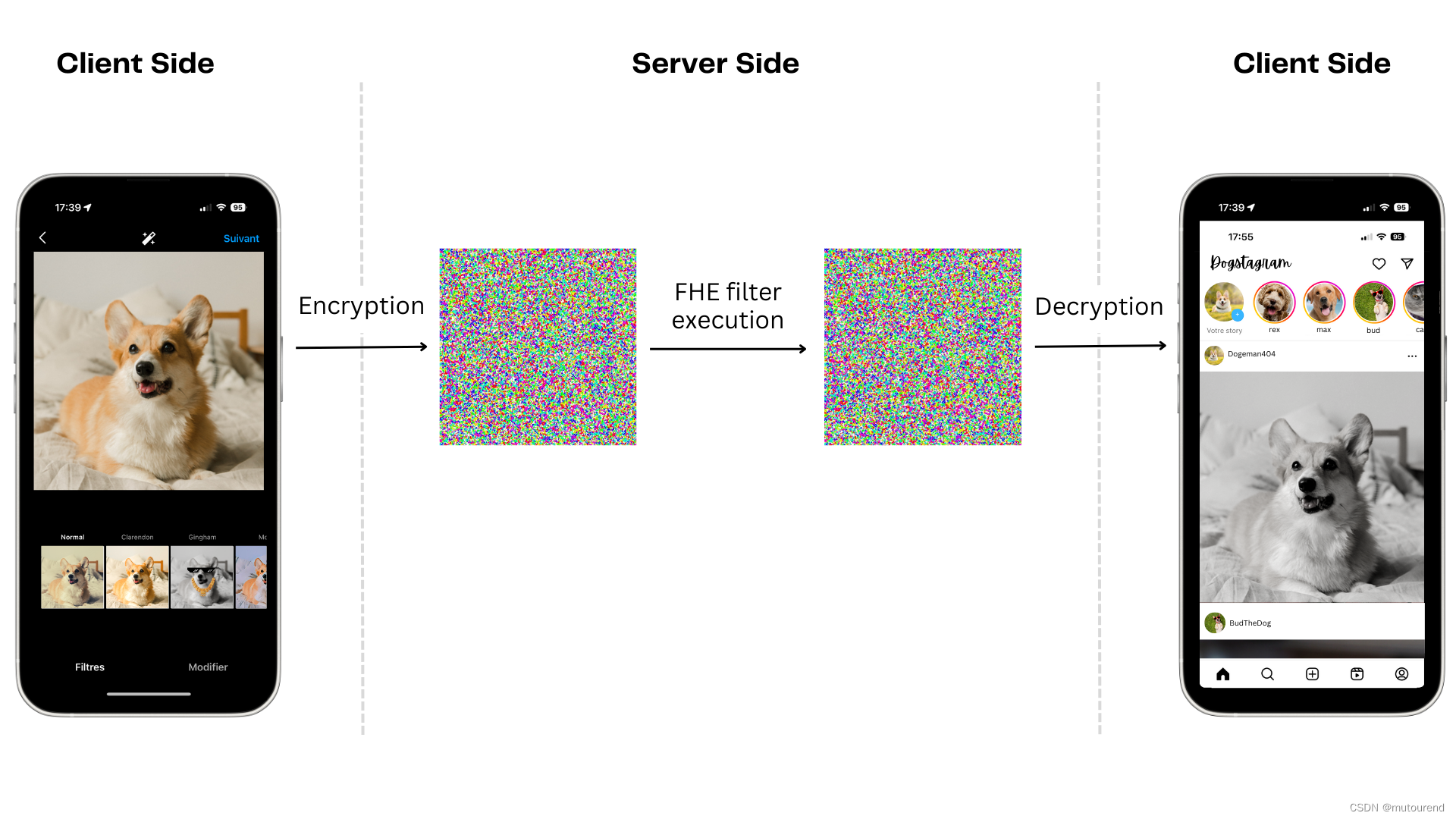
在这里插入图片描述

3.3 private smart contract

从设计上讲，区块链是公共的，这意味着流入web3应用程序的所有用户数据对整个世界都是可见的。有了FHE，可启用私人智能合约，其中的输入和输出是端到端加密的，这意味着你可以安全地构建使用敏感个人数据的去中心化应用程序，比如链上身份、私人NFT元数据或地理定位的Dapps。

如fhEVM：
在这里插入图片描述

fhEVM相应的private合约示例为：

contract EncryptedERC20 {
// A mapping from address to an encrypted balance.
mapping(address => euint32) internal balances;// Transfers an encrypted amount.
function _transfer(address from, address to, euint32 amount) internal {// Make sure the sender has enough tokens.TFHE.req(TFHE.le(amount, balances[from]));// Add to the balance of `to` and subract from the balance of `from`.balances[to] = TFHE.add(balances[to], amount);balances[from] = TFHE.sub(balances[from], amount);
}// Returns the balance of the caller encrypted under the provided public key.
function balanceOf(bytes32 publicKey,bytes calldata signature
) public view onlySignedPublicKey(publicKey, signature) returns (bytes memory) {return TFHE.reencrypt(balances[msg.sender], publicKey, 0);
}